III. PRINCIPIOS DE OPERACI�N DE LAS COMPUTADORAS ACTUALES
COMO ya se discuti� anteriormente, en los �ltimos a�os la computaci�n
ha tenido un desarrollo acelerado y ha contribuido en forma notable a la aparici�n
de nuevas tecnolog�as y a la organizaci�n de la sociedad. Este desarrollo se
ha llevado a cabo en un periodo muy corto de tiempo, de manera que la mayor
parte de las personas adultas hoy en d�a, crecieron teniendo poco o nulo contacto
con las computadoras, percat�ndose tiempo despu�s de la gran importancia que
�stas tienen, ya que est�n presentes en casi todos los aspectos de nuestras
vidas. Esto ha ocasionado que todo el mundo est� familiarizado con las computadoras,
pero que por otro lado, sean pocas las personas que tienen conocimiento de lo
que realmente son.
Existe todo un mito acerca de las capacidades de las computadoras, tanto que a menudo se mencionan cosas tan impresionantes como que �stas: "pueden calcular la explosi�n de una bomba de hidr�geno, analizar las ondas de choque y determinar la intensidad de la radiaci�n resultante; todo ello en relaci�n con las condiciones atmosf�ricas existentes durante la explosi�n", o tambi�n que "son capaces de predecir los resultados de una elecci�n antes de que se hayan juntado todas las boletas de los votantes", o bien que "pueden determinar las probabilidades de encontrar petr�leo en ciertos tipos de subsuelo",6 ![[Nota 6]](../imgs/mcommnt.gif)
etc. Este tipo de aseveraciones reflejan la creencia, bastante generalizada, de que las computadoras son capaces de llevar a cabo cualquier tarea con tan solo "ped�rselo".
La validez de esta afirmaci�n depende del significado que se confiera a la palabra "pedir", ya que las computadoras consisten en un complicado conjunto de circuitos electr�nicos, el cual es capaz �nicamente de llevar a cabo operaciones aritm�ticas y l�gicas, de la manera que m�s adelante explicaremos. Corresponde al programador dar a la computadora las instrucciones precisas para llevar a cabo un c�lculo o seguir un procedimiento. Debido a esto �ltimo, tenemos que la soluci�n a un problema depender� de los modelos o criterios utilizados por el programador para plantearlo. Por lo que los resultados s�lo ser�n correctos en la medida en que el modelo utilizado lo sea.
A continuaci�n diremos, en t�rminos generales, cu�les son los principios que utilizan las computadoras actuales para su funcionamiento y el tipo de operaciones que desempe�an. Esto, con el objeto de posteriormente hablar un poco acerca de los nuevos terrenos que la computaci�n ha empezado a explorar.
La ciencia de la computaci�n tiene que ver con la informaci�n: c�mo se representa, se procesa, se guarda y se transmite. Para ello se requiere de dos tipos de elementos que se conocen como circuiter�a y programas.7 La circuiter�a est� constituida por los elementos f�sicos de la computadora y de su equipo perif�rico, como son las impresoras, graficadoras, pantallas (monitores), cintas magn�ticas o discos duros para almacenar informaci�n, etc�tera. La circuiter�a del procesador central es tambi�n conocida con el nombre de arquitectura. Por otro lado, los programas est�n constituidos por las series de instrucciones que hacen posible el funcionamiento de la computadora.
Estos dos aspectos de las computadoras est�n estrechamente ligados, y se reflejan el uno en el otro, ya que la estructura de la computadora est� dise�ada de manera que �sta es capaz de ejecutar cierto tipo de tareas. Esto lo explicaremos a continuaci�n.
La mayor�a de las computadoras procesan y almacenan todos los datos y las instrucciones para procesarlos en forma de n�meros binarios. Esto es as� debido a que este sistema numeral es el m�s adecuado para ellas. Lo anterior puede ser f�cilmente comprendido si pensamos que para utilizar los n�meros en su forma decimal, las computadoras necesitar�an 10 niveles diferentes de voltaje para poder expresar 10 d�gitos. Por otro lado, los d�gitos binarios 0 y 1 pueden ser representados usando circuitos electr�nicos muy simples, que tan solo necesitan ser prendidos o apagados. Como consecuencia, tenemos que la �nica informaci�n que se puede manejar de esta manera se reduce a un "s�" o un "no". Esta cantidad de informaci�n es llamada bit, y es la unidad fundamental de todo dato. Las figuras 14 y 15 nos permiten apreciar la forma en que se representan los n�meros en las computadoras digitales.
Pero las computadoras no s�lo "representan" n�meros, sino que los procesan de acuerdo con las instrucciones recibidas; adem�s transfieren informaci�n de una parte a otra de ellas mismas, y de una m�quina a otra (v�ase la figura 16). Todas las instrucciones que estas m�quinas deben ejecutar son resumidas en programas, los cu�les son, en esencia, mensajes escritos de acuerdo con alg�n c�digo binario. Esto es, el lenguaje de m�quina tambi�n se expresa en t�rminos de bits.
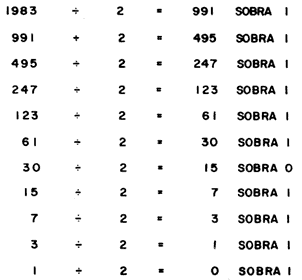
Figura 14. Este diagrama nos ilustra el procedimiento de divisiones sucesivas, utilizado para cambiar un n�mero de representaci�n decimal a su representaci�n binaria. El n�mero 1 983 est� representado por 11110111111, lo cual se obtiene al leer los residuos de las divisiones empezando por el �ltimo y teminando con el primero ( o sea de abajo hacia arriba).
Aunque el lenguaje de m�quina es el m�s adecuado para las computadoras, no lo es as� para el hombre. Si fuese necesario que nosotros utiliz�ramos dicho lenguaje para comunicarnos con las m�quinas, tendr�amos m�s problemas de los que intentamos resolver. Para dar soluci�n a este problema han sido creados los lenguajes de alto nivel, los cuales consisten en una serie de instrucciones que pueden ser entendidas, y aprendidas, tanto por el hombre como por las m�quinas. Dentro de la computadora, estos programas puente, comprensibles para el hombre, son traducidos al lenguaje de m�quina por programas llamados compiladores.8
Figura 15. Esta figura muestra la representaci�n binaria de los 10 d�gitos del sistema decimal. Cualquiera de estos n�meros puede ser representado mediante las diferentes combinaciones, abierto o cerrado, de cuatro interruptores.
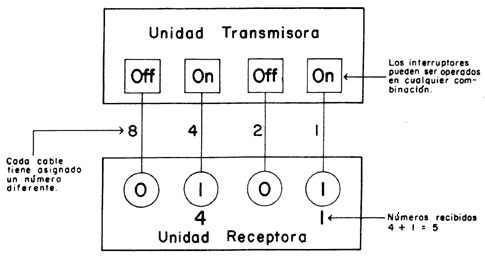
Figura 16. Transmisi�n del n�mero 4 utilizando cuatro cables, de acuerdo con la tabla de valores mostrada en la figura anterior.
Se han creado muchos lenguajes de alto nivel. Algunos lenguajes son m�s f�ciles de utilizar para el hombre que otros, o m�s simples, o m�s l�gicos, o mejor estructurados, o m�s compactos, o con caracter�sticas m�s apropiadas para llevar a cabo cierto tipo de trabajo, etc�tera, pero todos sirven para el mismo fin: facilitar la comunicaci�n hombre-m�quina. Entre los lenguajes m�s comunes tenemos el FORTRAN, el BASIC, el PASCAL, el "C", etc�tera.
Ahora bien, �de qu� manera se lleva a cabo el procesamiento de la informaci�n?, �c�mo puede un conjunto de interruptores llevar a cabo operaciones matem�ticas y procesar informaci�n tan compleja para as� contribuir a predecir, por ejemplo, los resultados de una explosi�n? La respuesta a estas preguntas est� en la adaptaci�n a las computadoras de un �lgebra especial, llamada �lgebra booleana, la cual fue creada a finales del siglo pasado con el objeto de hacer deducciones l�gicas utilizando para ello el lenguaje de las matem�ticas. A continuaci�n daremos una breve explicaci�n de los principios b�sicos del �lgebra booleana y de su aplicaci�n en las computadoras.
En 1847, un matem�tico ingl�s llamado Georg Boole public� un ensayo acerca del an�lisis matem�tico de la l�gica. En este documento estableci� un conjunto de axiomas a partir de los cuales pueden deducirse afirmaciones l�gicas m�s complicadas. Lo interesante del m�todo por �l introducido es la herramienta utilizada para llevar a cabo las deducciones: el �lgebra. Esto es, las proposiciones son escritas en t�rminos algebraicos mediante el uso de s�mbolos que representan ideas, y se llega a las deducciones por medio de operaciones algebraicas.
En otras palabras, esta �lgebra nos permite inferir, a partir de un conjunto de premisas, cu�les son las conclusiones a las que se puede llegar de una manera l�gica. Y dado que una conclusi�n puede ser verdadera o falsa (2 estados), esta �lgebra puede representarse mediante el uso de interruptores.
El �lgebra booleana est� basada en los siguientes principios: i) cualquier proposici�n �nica, simple o compleja, es llamada variable y est� representada por una letra del alfabeto; ii) existen ciertos s�mbolos que muestran las relaciones entre las proposiciones; y iii) estas relaciones pueden expresarse matem�ticamente. A continuaci�n explicaremos estos principios con algunos ejemplos:
Las proposiciones A, B, C y D pueden significar respectivamente: "mayor de 60 a�os", "m�s de veinticinco a�os de servicio", "jubilaci�n" y "jubilaci�n con salario completo". Por otro lado, las relaciones b�sicas entre las proposiciones son las siguientes: "OR" (O no exclusiva), "AND" (Y) y "NO" (NO).9 Estas relaciones se ilustran a continuaci�n.
A y B son dos afirmaciones independientes, entonces tenemos que la afirmaci�n conjunta
ser� verdadera si al menos una de las afirmaciones es verdadera. Esto es, la afirmaci�n A + B = C ser� verdadera si se trata de una persona ya sea mayor de 60 a�os o con 25 a�os de servicio. Por otro lado, si se trata de una persona que adem�s de ser menor de 60 a�os, tiene menos de 25 a�os trabajando, entonces la afirmaci�n ser� falsa (se trata de "OR" no exclusiva).
Ahora consideremos la afirmaci�n conjunta
Para que la afirmaci�n A · B = D sea verdadera, ser� necesario que la persona cumpla con ambos requisitos para obtener la jubilaci�n con salario �ntegro; esto es, deber� ser mayor de 60 y con m�s de 25 a�os de trabajo. Si alguna de las afirmaciones, o ambas, son falsas, entonces la proposici�n "A AND B" ser� falsa.
)
ser� cierta �nicamente si la persona en cuesti�n es menor de 60 a�os.
Pueden hacerse combinaciones m�s elaboradas de premisas, a partir de las relaciones b�sicas; as� como tambi�n es posible escribir una misma relaci�n de maneras diferentes. Por ejemplo:
B A= A + B
significa: tener a "todos los que tienen m�s de 60 a�os de edad o que tienen m�s de 25 a�os de antig�edad" es lo mismo que tener a todos los que son mayores de 60 a�os o que adem�s de ser menores de 60 a�os tienen m�s de 25 a�os de antig�edad. N�tese que aun con relaciones muy simples como �sta se vuelve dif�cil traducirlas al lenguaje com�n, y m�s a�n, efectuar deducciones. Esto nos muestra que una de las grandes ventajas de reducir operaciones l�gicas a t�rminos de operaciones matem�ticas es que, a diferencia del lenguaje com�n, las matem�ticas no tienen ambig�edades. La figura 17 nos muestra un resumen de las leyes del �lgebra booleana, las cuales nos son �tiles para simplificar expresiones.
Para utilizar el �lgebra booleana en la computadora, se le asigna el valor
"1" a la palabra VERDADERO, y el valor 0 a FALSO,
o "prendido" y "apagado", respectivamente, y se construyen circuitos electr�nicos
dentro de la computadora, que se comportan al igual que estas funciones l�gicas.
�stos son los llamados circuitos l�gicos9
(v�ase la figura 18). De esta manera, cuando la computadora ejecuta un programa,
env�a la informaci�n a los circuitos compatibles con el tipo de operaci�n que
se desea efectuar. Por otro lado, las figuras 19 y 20 muestran los s�mbolos
convencionales y las tablas de verdad para algunos circuitos simples.
Por supuesto, no es necesario construir un circuito especial para cada problema que deseamos resolver, ya que cualquier problema expresable en t�rminos matem�ticos, por complicado que sea, puede realizarse por partes en las diferentes unidades encargadas de efectuar operaciones. Dentro del cerebro central de una computadora existe un gran n�mero de circuitos l�gicos, algunos de ellos de gran complejidad; cada uno de estos circuitos ha sido dise�ado para llevar a cabo cierta operaci�n l�gica espec�fica, dependiendo de su arquitectura (Figura 21). Es papel del procesador central el controlar c�mo y cu�ndo deben efectuarse las operaciones, y transferir los datos e instrucciones a las unidades encargadas de llevarlas a cabo.
|
Absorción : A + ( A + B ) = A A · ( A + B ) = A |
Distribución : A · ( B + C ) = ( A · B ) + ( A · C ) A + ( B · C ) = ( A + B ) · ( A + C ) |
|
Anulamiento : A + 1 = 1 A · 0 = 0
|
Doble negación :
|
|
Asociación : ( A + B ) + C = A + ( B + C ) ( A · B ) · C = A · ( B · C ) |
Dualidad : Principio útil ( en realidad no se trata de una regla) : Y = A · B equivale a Y = A + B equivale a |
|
Conmutación : A + B = B + A A · B = B · A |
Identidad : A + 0 = A A · 1 = A |
|
Complementos : A + A · |
Tautología : A · A = A A + A = A |
|
de De Morgan :
|
=
A
= 
= 
= Figura 17. Resumen de las leyes del �lgebra booleana.
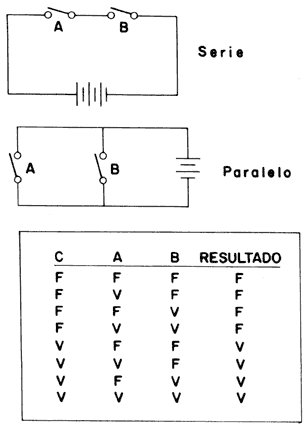
Figura 18. Circuitos que representan funciones l�gicas, a) funci�n AND ("Y"): a y B deben estar cerrados para que la corriente circule a trav�s del circuito; esto es, A � B = VERDADERO �nicamente si A=VERDADERO y B=VERDADERO; b) funci�n OR ("O") : el circuito quedar� cerrado a condici�n de que la corriente circule, ya sea por A, por B o por ambas, esto es , si A= VERDADERO o B= VERDADERO. Las tablas de verdad para estos dos circuitos se incluyen en la fig. 19.
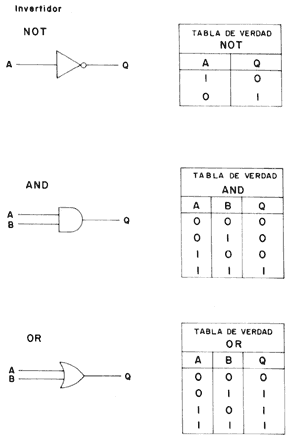
Figura 19. En esta figura se muestran los s�mbolos convencionales y tablas de verdad para los circuitos elementales NOT, AND y OR. Las tablas de verdad de un circuito est�n formadas por las partes de �ste ante todas las combinaciones de "FALSO" y "VERDADERO" de las funciones de entrada.
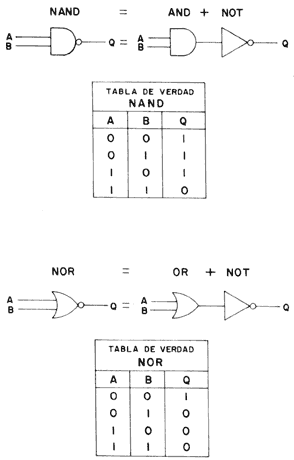
Figura 20. S�mbolos convencionales y tablas de verdad para los circuitos compuestos NAND y NOR.
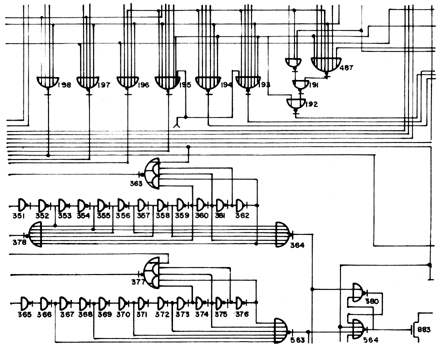
Figura 21. El primer paso para la construcci�n de un circuito es su dise�o.
PRINCIPALES COMPONENTES DE UNA COMPUTADORA
Desde el punto de vista operativo, una computadora electr�nica digital puede ser representada esquem�ticamente por tres subsistemas. �stos son: la unidad de entrada y salida de datos, la unidad central de procesamiento y finalmente, lo que nos ocupa en este libro, la memoria.
La unidad de entrada y salida de datos sirve como enlace entre la computadora y el exterior. Como su nombre lo indica, tiene dos funciones: la primera consiste en permitir la entrada de los programas, datos e instrucciones a la computadora, y la segunda es permitir la salida de la informaci�n, una vez que �sta ha sido procesada, ya sea hacia el usuario de la m�quina, hacia otras computadoras, o hacia alg�n otro dispositivo.
La unidad central de procesamiento es el cerebro de la computadora y est� encargada de controlar su funcionamiento integral. Esto es, lee los programas de la memoria, transfiere informaci�n de una parte a otra de la m�quina, lleva a cabo c�lculos necesarios y las operaciones requeridas por el programa, y controla los dispositivos asociados con la computadora.
Finalmente, las memorias son dispositivos utilizados para almacenar informaci�n en las computadoras, y se denomina memorizaci�n al proceso por medio del cual se modifica el la memoria. Esta modificaci�n se lleva a cabo de acuerdo con un c�digo, de manera que el nuevo estado del dispositivo representa la informaci�n que ha sido almacenada.
Una de las funciones m�s importantes de las computadoras es el almacenamiento de grandes bancos de datos. Pero las memorias no sirven �nicamente para este prop�sito. Ellas son parte esencial de las computadoras, sin la cual no ser�a posible el procesamiento de la informaci�n, ya que funcionan como gavetas en las cuales se guarda, de una manera ordenada, todo el material mientras �ste no es utilizado. Las memorias pueden clasificarse con base en su funci�n o conforme a sus caracter�sticas. De acuerdo con la primera clasificaci�n, se dividen en memoria principal o de trabajo y memoria secundaria o auxiliar.
La memoria principal almacena temporalmente los programas que se est�n "ejecutando"
o est�n en proceso de hacerlo, as� como los datos, antes y despu�s de ser procesados.10
Esta
memoria puede ser complementada con memoria secundaria o auxiliar, generalmente
en forma de cinta o discos magn�ticos, los cuales se encuentran f�sicamente
fuera de la computadora. Este tipo de memoria puede guardar de manera semipermanente,
y por un tiempo indefinido, toda la informaci�n que deseemos conservar. Por
lo general se utiliza para guardar grandes cantidades de informaci�n. La cantidad
de informaci�n almacenable mediante el uso de memorias auxiliares es pr�cticamente
ilimitada, sin embargo �sta se recupera con mucha lentitud en comparaci�n con
la almacenada en la memoria principal.
Por otro lado, de acuerdo con sus caracter�sticas, existen varios tipos de memorias, cada uno de los cuales ofrece ventajas y desventajas frente a los otros, por lo cual resultan ser m�s apropiados para una u otra tarea. Generalmente en estas memorias se puede leer y escribir informaci�n, aunque hay memorias en las cuales la informaci�n almacenada no puede ser alterada, esto es, �nicamente puede leerse. Entre las memorias mejor conocidas, se encuentran las memorias de anillos magn�ticos, las memorias semiconductoras y las memorias de burbujas magn�ticas.
Las memorias de anillos magn�ticos est�n formadas por un arreglo de anillos de ferrita, cada uno de los cuales es magnetizable en una de dos direcciones; de manera que puede representar un bit de informaci�n. La figura 22 muestra este tipo de memoria. Por otro lado, las memorias semiconductoras consisten en circuiter�a integrada a diferentes escalas. Las memorias de muy grande escala de integraci�n son muy compactas, ya que un chip de silic�n de medio cent�metro de largo puede contener cientos de miles de circuitos microelectr�nicos, cada uno de los cuales guarda un d�gito binario. Algunas memorias semiconductoras son vol�tiles, esto es, en cuanto se interrumpe el suministro de energ�a el�ctrica, se borra la informaci�n almacenada.
Todas estas memorias guardan la informaci�n de una manera conceptualmente igual, aunque t�cnicamente la forma de construirlas sea diferente. La idea es la siguiente: las memorias est�n formadas por un gran n�mero de celdas individuales de almacenamiento, cada una de las cuales es capaz de retener un n�mero binario. Estas celdas se agrupan en localidades o palabras, constituidas por un cierto n�mero de celdas b�sicas; este n�mero var�a de una m�quina a otra, siendo las palabras de ocho bits (conocidas como bytes) las m�s com�nmente utilizadas. Por �ltimo a cada palabra se le asigna una identificaci�n num�rica, o direcci�n, la cual sirve para se�alar la posici�n de la palabra dentro del dispositivo, para as� tener acceso a la informaci�n en ella contenida. La capacidad o tama�o t�pico de las memorias de las computadoras personales de hoy en d�a es del orden de kilobytes, K, por ejemplo 16k, 32 k, 64 k, etc�tera (1 kilobyte es aproximadamente igual a 1 000 bytes)
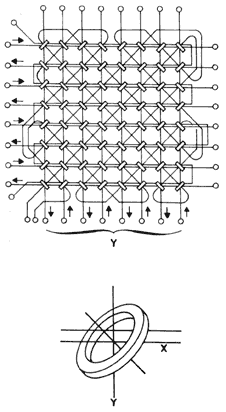
Figura 22. Memoria de anillos magn�ticos. En este tipo de memoria, cada anillo es del tama�o de una cabeza de alfiler, y es capaz de guardar un bit de informaci�n. Actualmente, este tipo de memorias ha sido substituido por las memorias semiconductoras.
En el pr�ximo cap�tulo compararemos esta forma de almacenamiento de informaci�n
con la que se piensa que utilizan los seres vivos. Ambas formas de almacenamiento
son esencialmente diferentes, lo cual se refleja en su eficiencia en el desempe�o
de diversos tipos de tareas.
