X. PARA ATRAPAR UN FOTÓN

LA COMPOSICIÓN granular de la luz, demostrada de múltiples formas, algunas de las cuales hemos descrito anteriormente, no puede ser puesta en duda. También queda demostrado por los descubrimientos de Einstein que la luz no es emitida por ondas esféricas. Sin embargo, el éxito de la óptica ondulatoria para explicar los fenómenos de refracción, difracción e interferencia de la luz no puede ser ignorado; así como tampoco puede pasar inadvertida la relación que establece la ecuación de Planck E=hf entre las "partículas de luz", o fotones, y alguna onda que tiene la frecuencia f. Esto es, el movimiento de los corpúsculos de luz, o fotones, debe estar asociado a la onda electromagnética que determina su energía y, en muchos experimentos, determina también su comportamiento.

¿Cómo es posible la difracción de la luz por una ranura si la suponemos compuesta por fotones indivisibles? Ya vimos que si intentamos medir el diámetro de los fotones cerrando la ranura hasta permitir apenas su paso, encontramos que éstos pasan por las ranuras más estrechas; de manera que no es posible asignarles una dimensión definida. Sin embargo, alguna propiedad del fotón debe estar relacionada con una longitud puesto que éste distingue una ranura estrecha en la que es difractado, de una ranura ancha por la que transita sin desviarse. La óptica ondulatoria, por su parte, establece que una ranura produce difracción sólo si su anchura es comparable con la longitud de onda de la luz; es decir, si la anchura es, cuando mucho, unas cuantas veces mayor que la longitud de onda. Esto implica que alguna propiedad del fotón debe estar relacionada con la longitud de una onda. La ecuación de Planck, E=hf, muestra esta relación. Si escribimos la frecuencia f como la velocidad de la luz c dividida entre la longitud de onda L, la ecuación de Planck queda escrita en la forma E=hc/L que relaciona una propiedad del fotón, la energía, con la longitud de una onda. Esta onda debe ser la onda electromagnética que producen las cargas eléctricas en movimiento, junto con el fotón.

Podemos intentar ahora hacernos una representación más completa de lo que ocurre en la producción de un fotón. Según el resultado de Einstein, el fotón es producido en un tiempo muy breve, como de una milmillonésima de segundo, por la agitación momentánea de las cargas eléctricas de una molécula; además, es emitido a la velocidad de la luz, pero no como una onda esférica, sino en una dirección bien definida. Simultáneamente las cargas producen una onda electromagnética que se propaga, también a la velocidad de la luz, junto con el fotón. La onda puede ser esférica o no, esto depende sólo del movimiento de las cargas, pero su extensión es limitada. La onda ocupa sólo la distancia que viaja la luz durante el movimiento de las cargas. Por ejemplo, si el tiempo de emisión fuera de una milmillonésima de segundo, la extensión de la onda sería una milmillonésima parte de los 300 000 km que viaja la luz cada segundo; o sea, sería de 30 cm. Una onda de extensión limitada se llama "tren de ondas" y se representa como en la figura 40. Como la longitud de onda de la luz es tan pequeña, en el tren caben muchísimas ondas completas. Si la longitud de onda de la luz en el ejemplo anterior fuera de 0.00005 cm, en el tren cabrían 30/ 0.00005=600 000 ondas completas. La frecuencia de la onda es el número de oscilaciones en un segundo; o sea, f=600 000/ 0.000000001=600 billones de hertzios. La energía del fotón emitido depende de la frecuencia de esta onda.

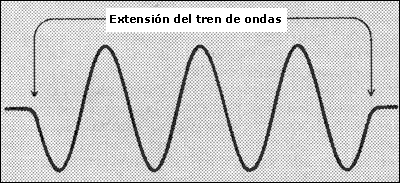
Figura 40. Un tren de ondas es una onda de extensión limitada.

El tren de ondas electromagnéticas es generado con el fotón, pero no es el fotón. Éste puede ser encontrado en cualquier lugar de la región ocupada por el tren de ondas, pero no está repartido sobre toda esta región; si se le encuentra en algún lugar, se le encuentra completo. Por ejemplo, si el tren fuera esférico, el fotón podría encontrarse, completo, en cualquier parte de un cascarón esférico de 30 cm de espesor y con un radio que aumenta a la velocidad de la luz. En este cascarón se encuentra el tren de ondas generado por el movimiento de las cargas (Figura 41). En otras palabras, el tren de ondas electromagnéticas indica dónde puede ser encontrado, pero no dónde está el fotón. Por ejemplo, si este tren de ondas esféricas llega a una ranura delgada, atrás de ella ya no se propaga como una onda esférica, sino que debido a interferencias en la onda trasmitida, se forman zonas de interferencia destructiva, donde la onda electromagnética se cancela por completo, y zonas de interferencia constructiva donde la interferencia refuerza la intensidad de la onda. Éstas son las zonas que se observan en la difracción de la luz por una ranura (Figuras 17 y 18). Si se ilumina la ranura con luz tan débil que los fotones pasen uno por uno por ella, cada uno de ellos podría ser encontrado en los lugares de interferencia constructiva, pero no podrá ser encontrado en los lugares de interferencia destructiva. Esto se comprueba recibiendo los fotones en una placa fotográfica. Los puntos marcados en la película por los fotones trasmitidos caen, uno por uno, en los lugares de interferencia constructiva de la onda y ningún punto cae en los lugares donde las interferencias anulan la intensidad de la onda trasmitida. Más aún, los puntos se acumulan más rápidamente en la banda central del patrón de difracción que en las laterales, indicando que los fotones prefieren llegar a los lugares donde la onda electromagnética es más intensa.

Figura 41. Un tren de ondas electromagnéticas esféricas producido al generarse un fotón por el movimiento de las cargas en un átomo. El fotón puede encontrarse, completo, en cualquier parte del tren con igual probabilidad.

El experimento de Young de la ranura doble comprueba esta relación del fotón con la onda electromagnética. El patrón de iluminación de la ranura doble difiere del de la ranura sencilla fundamentalmente en las imágenes brillantes de interferencia que aparecen al centro (Figura 21). Necesitamos ahora explicar cómo se forman estas imágenes de interferencia con los fotones que componen la luz que llega a la ranura doble. Puesto que los fotones son indivisibles, cada fotón pasa sólo por una de ellas. Si la ranura por la que no pasa un fotón no tuviera ningún efecto, todos los que pasan por una ranura producirían un patrón de difracción independiente del producido por los que pasan por la otra y no habría interferencia entre ellos. Se observaría solamente la superposición de dos patrones de difracción de una ranura y las imágenes brillantes centrales de interferencia constructiva no se observarían. Las dos ranuras influyen en cada fotón porque ambas trasmiten la onda electromagnética asociada a cada uno de ellos. Atrás de las ranuras se producen entonces zonas de interferencia constructiva donde un fotón que pase por cualquier ranura puede ser encontrado, y zonas de interferencia destructiva donde cualquier fotón trasmitido no puede ser encontrado. Cada fotón trasmitido tiene mayor probabilidad de llegar a las zonas centrales donde la intensidad de la onda trasmitida es grande debido a la interferencia constructiva, y una menor probabilidad de llegar a las zonas intermedias y laterales, donde la intensidad de la onda trasmitida es pequeña debido a la interferencia destructiva.

Todavía se podría pensar que las imágenes centrales observadas con la ranura doble resultan de interacciones directas entre los fotones que se encuentran en tránsito por las ranuras. Esto es, que los fotones, de alguna manera, alterarían mutuamente sus movimientos agrupándose en algunas regiones y alejándose de otras. Esta posibilidad fue eliminada en 1909 por el físico inglés G. I. Taylor, quien realizó el experimento de la ranura doble de Young con fuentes luminosas extraordinariamente débiles, de manera que los fotones pasaban uno a uno por la ranura doble y no existía posibilidad de que se influyeran mutuamente en sus movimientos. Los fotones trasmitidos eran recibidos en la película de una cámara fotográfica imprimiendo cada uno un punto en el sitio de su llegada. Acumulando puntos durante tiempos muy largos, en ocasiones durante varias semanas, se encontró que siempre forman las mismas imágenes de interferencia que se observan con fuentes de luz más intensas.

Esto demostró que las imágenes no pueden resultar de influencias mutuas entre los fotones y apoya la hipótesis de que cada fotón trasmitido puede llegar a cualquier lugar donde la intensidad de la onda no se anule. Los fotones, desde luego, llegan con mayor probabilidad a las zonas donde la intensidad de la onda electromagnética trasmitida es grande y no llegan a las zonas donde esta intensidad se anula por interferencias destructivas.

Para atrapar un fotón conviene, pues, buscarlo en las zonas de mayor intensidad de la onda electromagnética. Por ejemplo, para atraparlo después de pasar por una ranura doble, podemos hacer un diagrama de Young de las ondas trasmitidas por las ranuras, como el de la figura 23, y localizar las zonas donde interfieren constructivamente; éstas son las regiones más oscuras que se ven mirando el diagrama en un ángulo oblicuo desde el lado derecho hacia el izquierdo de la figura 42. Un fotón trasmitido por cualquiera de las ranuras puede ser atrapado, con gran probabilidad, en cualquiera de estas zonas. No es posible, sin embargo, saber anticipadamente en cuál será encontrado; puede llegar a cualquiera de ellas con la misma probabilidad. Tampoco es posible asegurar, una vez atrapado el fotón, por cuál de las dos ranuras fue trasmitido; pudo ser cualquiera de las dos con la misma probabilidad.

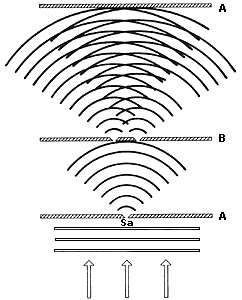
Figura 42. Diagrama de Young para encontrar las zonas de interferencia constructiva de las ondas transmitidas por dos ranuras. Éstas son las regiones oscuras que se notan viendo el diagrama oblicuamente desde el extremo derecho hacia el izquierdo. Un fotón de la luz transmitida por las ranuras puede llegar, con gran probabilidad, a cualquiera de esas zonas.

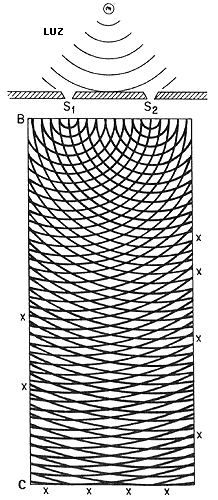
Figura 42. (b)

Este ejemplo muestra que generalmente no es sencillo saber dónde ocurren las zonas de interferencia constructiva de ondas que encuentran obstáculos porque las ondas trasmitidas, o reflejadas, se combinan en el espacio creando zonas de interferencia de formas complicadas. El ejemplo de la ranura doble es de los más sencillos y requiere de trazar un esquema a escala de la posición de las ranuras, y muchos semicírculos concéntricos equidistantes que representan las ondas trasmitidas por las ranuras. Las zonas de interferencia constructiva de ondas trasmitidas por dos o más ranuras se pueden encontrar más fácilmente trazando los juegos de semicírculos equidistantes correspondientes a cada ranura, en hojas de plástico transparentes como las mostradas en la figura 43. Por ejemplo, las zonas creadas por una ranura doble se observan sobreponiendo dos de estas hojas en un papel blanco de manera que las bases de los semicírculos queden sobre una misma recta con los centros ligeramente separados. Las zonas de interferencia constructiva de las ondas trasmitidas están representadas, como antes, por las regiones oscuras que se forman en las intersecciones de los semicírculos. Cambiando la separación entre los centros de los dos juegos de semicírculos se puede ver cómo cambian las regiones de interferencia constructiva al cambiar la distancia entre las ranuras. Este método se puede emplear también para más de dos ranuras, sobreponiendo más láminas; o para ranuras que no se encuentren sobre el mismo plano, colocando las bases de los semicírculos sobre rectas que formen un ángulo igual al de los planos de las ranuras.

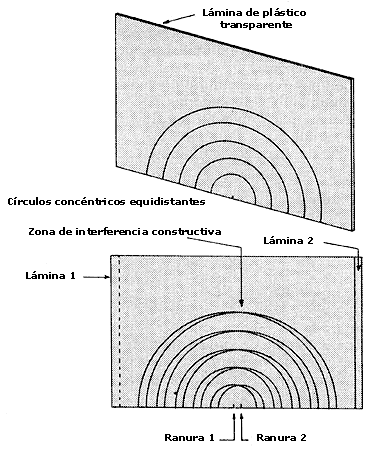
Figura 43. Diagrama de Young para dos ranuras, construido con láminas de plástico transparente sobrepuestas en un papel blanco. En cada lámina se representa la onda esférica propagada desde una ranura con una serie de semicírculos equidistantes. Cambiando la separación de los centros de las láminas se observa cómo cambian las zonas de interferencia constructiva de las ondas transmitidas.