IV. REFLEXI�N Y REFRACCI�N DE LA LUZ

LA HIP�TESIS de los rayos rectos luminosos no es la �nica hip�tesis de la �ptica geom�trica. Para explicar el fen�meno de la reflexi�n de la luz (Figura 4) es necesario suponer que la direcci�n de los rayos luminosos cambia en algunas circunstancias. Una imagen en un espejo se ve como si el objeto estuviera atr�s, y no frente a �ste. La �ptica geom�trica explica este familiar fen�meno suponiendo que los rayos luminosos cambian de direcci�n al llegar al espejo. La forma precisa en que ocurre este cambio se conoce como ley de la reflexi�n de la luz. Es una ley muy sencilla: los rayos incidente y reflejado hacen �ngulos iguales con el espejo; o con la perpendicular al espejo, que es como suelen medirse estos �ngulos (Figura 10). Esta ley, por cierto, tambi�n se puede deducir aplicando la ley de variaci�n del tama�o aparente con la distancia para explicar los tama�os aparentes de un objeto y de su imagen en un espejo plano. O, dicho de otra forma, si vemos nuestra imagen en un espejo plano del tama�o que la vemos es porque los rayos incidente y reflejado forman �ngulos iguales con el espejo.

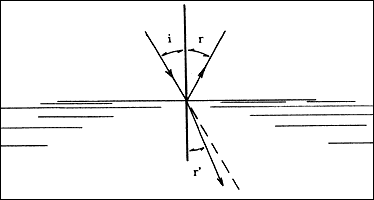
Figura 10. La ley de la reflexi�n de la luz: el �ngulo de incidencia, i, y el de reflexi�n, r, de un rayo luminoso sobre una superficie son iguales; esto es i = r.

La ley de la refracci�n de la luz: el seno del �ngulo de incidencia, sen i, y el seno del �ngulo de refracci�n, sen r', de un rayo luminoso que atraviesa la superficie de separaci�n de dos medios transparentes est�n en las misma proporci�n para cualquier valor del �ngulo i; esto es, sen i /sen r' = n. Si la luz pasa de aire al agua, sen i /sen r' = 4/3.

Un cuerpo parcialmente sumergido en agua se ve chueco; como si se doblara al entrar al agua. Este fen�meno se llama refracci�n. Adem�s del agua se observa en muchos otros medios transparentes, como el vidrio, llamados refringentes. Era uno de los problemas �pticos pendientes de soluci�n todav�a hacia el siglo XIII (Figura 4). Los fen�menos de refracci�n se incorporan a la �ptica geom�trica simplemente suponiendo que los rayos luminosos cambian de direcci�n no s�lo al reflejarse sino tambi�n al pasar de un medio refringente a otro; por ejemplo, del agua al aire, o del agua al vidrio, o del vidrio al aire. Un experimento sencillo que demuestra este cambio de direcci�n se muestra en la figura 11. Una moneda peque�a en el fondo de una taza vac�a est� apenas oculta por el filo de la taza en la figura 11 (a). Llenando lentamente la taza con agua la moneda aparece poco a poco, hasta observarse por completo, en la figura 11(b). Los rayos luminosos emitidos por la moneda que llegan al ojo debido a que son refractados en la superficie del agua se muestran en esa figura; la moneda se ve en la direcci�n de estos rayos. El experimento muestra tambi�n que los rayos refractados est�n m�s cerca de la superficie en el medio menos denso; el aire en la figura 11(b).

Figura 11. Un experimento para demostrar la refracci�n de la luz. En (a) la moneda est� apenas oculta por una orilla de la taza. En (b) la moneda aparece al llenar lentamente la taza con agua. Los rayos luminosos cambian de direcci�n al pasar del agua al aire.

La forma precisa en que cambia la direcci�n de los rayos en la refracci�n, esto es, la ley de la refracci�n, no es tan simple como la ley de la reflexi�n. Tal vez por esto, aunque el fen�meno de la refracci�n era conocido desde la antig�edad, la ley de la refracci�n no fue descubierta sino hasta el siglo XV por el astr�nomo holand�s Willebrord Snell, quien, inexplicablemente, no la dio a conocer, describi�ndola solamente en sus notas personales de investigaci�n. La ley de la refracci�n fue divulgada por Descartes en 1627, pero se conoce universalmente como la ley de Snell. No relaciona los �ngulos de los rayos luminosos con la perpendicular a la superficie de refracci�n, sino los senos de esos �ngulos. En s�mbolos matem�ticos se expresa as�: sen (i) / sen (r') = constante = n; esto es, el cociente de los senos de los �ngulos de incidencia i y de refracci�n r' toma el mismo valor para todos los valores posibles de estos �ngulos. Por ejemplo, si los rayos pasan del aire al agua la cantidad constante n, llamada �ndice de refracci�n, vale 4/ 3 y se tiene sen (i) / sen (r') = 4/ 3.

La ley de la refracci�n de la luz tambi�n puede ser deducida aplicando la ley de variaci�n del tama�o aparente con la distancia. La figura 12 muestra un sencillo experimento para hacer esto. Dos monedas peque�as se ponen en dos tazas, una vac�a y la otra parcialmente llena de agua. Observ�ndolas desde arriba y a la misma altura, la moneda sumergida en agua se ve m�s grande debido a que por la refracci�n de la luz los rayos que emite se abren m�s al pasar por la superficie del agua y llegan al ojo como si hubieran sido emitidos por una moneda m�s cercana. De los tama�os aparentes de las dos monedas se deducen los �ngulos que forman los rayos con la perpendicular a la superficie; el de los rayos refractados depende de la altura de llenado de la taza. Los senos de estos �ngulos se obtienen de una tabla de valores y dividiendo el mayor entre el menor se encuentra que su cociente siempre es 4/ 3, el �ndice de refracci�n del agua; independientemente de la altura de llenado de la taza.

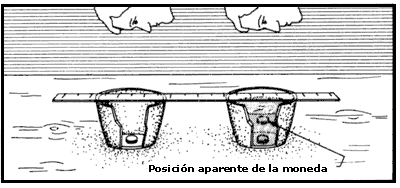
Figura 12. Un experimento para comprobar la ley de la refracci�n. La moneda sumergida en el agua se ve m�s grande porque los rayos que parten de ella se abren al salir al aire y parecen llegar de una moneda m�s cercana. Relacionando los tama�os aparentes con los �ngulos de los rayos se obtiene la ley de la refracci�n, o ley de Snell.

La hip�tesis de los rayos luminosos y las leyes de la reflexi�n y de la refracci�n de la luz son el fundamento de la �ptica geom�trica. Con ellas es posible predecir el curso que tomar�n los rayos luminosos que lleguen a lentes o a espejos. Por ejemplo, en la figura 13, los rayos que llegan de un punto luminoso a la lente de una lupa com�n son divergentes, pero se hacen convergentes al atravesarla debido a las refracciones que ocurren en las dos superficies del vidrio. Despu�s de alcanzar el punto de convergencia los rayos vuelven a ser divergentes, de manera que si los vemos desde un lugar m�s lejano a�n, los percibimos como si se originaran en el punto de convergencia; es decir, como si el objeto hubiera sido transportado a ese lugar. Se dice que en este punto se forma una imagen real del objeto. Las leyes de la refracci�n permiten calcular el lugar preciso donde se forma esa imagen. Mirando con otra lupa en ese lugar se observa la imagen amplificada del objeto. As� es, esencialmente, como funciona un telescopio (Figura 14). Este instrumento utiliza dos lentes del tipo llamado convergente, parecidas a la de una lupa en que son m�s gruesas enmedio que en la orilla. La primera de ellas —llamada objetivo— produce una imagen real de un objeto lejano, como la Luna, en un punto atr�s y cerca de la lente. La segunda lente del telescopio, llamada ocular, se usa simplemente como una lente de aumento com�n para amplificar y observar esta imagen (Figura 14).

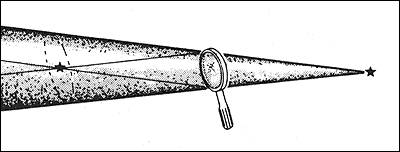
Figura 13. Una lupa intercepta rayos divergentes emitidos por un punto luminoso y los re�ne en otro punto. Los rayos reunidos parecen salir de este lugar. Se dice que aqu� se forma una imagen real del punto luminoso.

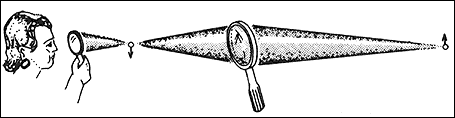
Figura 14. Un telescopio sencillo se compone de una lente, llamada objetivo, que forma cerca de ella una imagen real de un objeto lejano, y de una lente de aumento, llamada ocular, con la que se examina esta imagen.

Resumiendo lo anterior, la �ptica geom�trica est� compuesta por una hip�tesis, la de los rayos rectos luminosos; por dos leyes derivadas de la experiencia, la de la reflexi�n y la de la refracci�n de la luz, y por una ciencia matem�tica, la geometr�a, con la que se puede aplicar met�dicamente a los problemas �pticos. La �ptica geom�trica ha sido extraordinariamente fruct�fera por estar basada en leyes que se cumplen con precisi�n y en una ciencia tan completa como la geometr�a, pero parte de su �xito es resultado de su hip�tesis principal. Es decir, aunque no se ha intentado siquiera aclarar de qu� est�n hechos los rayos luminosos, deben estar hechos de algo que se propaga como esos rayos; de otra manera la teor�a no habr�a tenido tanto �xito.

Isaac Newton supon�a que los rayos luminosos est�n compuestos por part�culas extraordinariamente diminutas que los cuerpos luminosos arrojan a gran velocidad y que al penetrar al ojo e incidir sobre la retina estimulan la visi�n. Newton apoyaba estas ideas en el fen�meno de la propagaci�n rectil�nea de la luz, pues s�lo suponi�ndola compuesta por part�culas independientes pod�a imaginar que los rayos de luz pudieran ser separados unos de otros por medio de un popote como en la figura 1, o de una lente convergente como en la figura 13. Otro importante argumento que Newton daba en apoyo a esta idea era que la luz no da la vuelta a cuerpos opacos; o bien, que la sombra geom�trica de un cuerpo est� limitada por l�neas rectas como en la figura 7. Este argumento se esgrim�a principalmente en contra de las ideas de Descartes, quien supon�a que la luz era una "especie de presi�n" propagada alrededor de los cuerpos luminosos que al llegar al ojo estimulaba la visi�n. Pero, arg��a Newton, una zona de presi�n como �sta no tendr�a por qu� no propagarse alrededor de los cuerpos y entrar en la sombra geom�trica; esto es, si la luz fuera causada por esas "zonas de presi�n", tambi�n deber�a percibirse en la sombra geom�trica de cuerpos opacos.

Las ideas de Newton desembocaban tambi�n en importantes conclusiones al aplicarlas a la refracci�n de la luz. La figura 15 intenta explicar la refracci�n estudiando el movimiento de una pelota de tenis. Debido a que la velocidad de la pelota es diferente en el agua que en el aire, la direcci�n de su movimiento cambia al atravesar la superficie; esto es, se refracta. Y se puede demostrar que si la velocidad en el agua es menor que en el aire el �ngulo de refracci�n r' es mayor que el de incidencia i, como aparece en esa figura. Pero en la refracci�n de la luz ocurre precisamente lo contrario, el �ngulo de refracci�n es menor que el de incidencia al pasar del aire al agua, o al pasar a cualquier otro medio m�s denso como, por ejemplo, el vidrio. Es, entonces, inevitable concluir que, si estuviera compuesta por part�culas, la luz ser�a m�s r�pida en los medios m�s densos. En particular, deber�a ser m�s r�pida en cualquier medio transparente que en el vac�o. En tiempos de Newton (1642-1727) s�lo era posible medir la velocidad de la luz por medios astron�micos y de ninguna manera en un laboratorio, como hubiera sido necesario para medirla en agua, o en vidrio, y comparar este valor con el ya conocido para el vac�o. Por este camino, pues, no fue posible adentrarse en el conocimiento de la naturaleza de los rayos luminosos por muchos a�os.

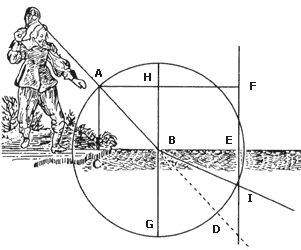
Figura 15. La velocidad de una pelota de tenis disminuye y la direcci�n de su movimiento se acerca a la superficie al entrar al agua. La luz, por el contrario, al entrar al agua se aleja de la superficie. De esto se deduce que, si la luz estuviera formada por part�culas, �stas se mover�an m�s r�pidamente en agua que en aire.