VIII. MICHAEL FARADAY, DIAMAGNETISMO Y EL EFECTO HALL CUÁNTICO

LEOPOLDO GARCÍA-COLÍN SCHERER

INTRODUCCIÓN

"POR mucho tiempo he sido de la opinión, que casi llega al grado de una convicción, de creer, en acuerdo con muchos otros estudiosos de la naturaleza que las varias formas bajo las cuales se ponen de manifiesto las fuerzas de la materia tienen un origen común; en otras palabras, que están relacionadas entre sí de manera tal que son mutuamente dependientes y son convertibles unas en otras, como si fueran y poseyeran equivalencias de potencia en su acción." Con este párrafo Michael Faraday, el notable físico y químico inglés, considerado por muchos como uno de los científicos experimentales más versátiles del siglo pasado, comienza su artículo titulado "Acción de los imanes sobre la luz", publicado en el Philosophical Transactions (Londres) en 1846 [1]. En este trabajo Faraday resume sus largas experiencias, iniciadas en 1831 que versan sobre la evolución de la electricidad, el magnetismo y que, entre otros descubrimientos, lo condujeron a entender el fenómeno de la inducción. El objetivo que se persigue aquí es explicar el éxito que se logró al describir la "electrificación y magnetización de un haz de luz y en iluminar una línea de fuerza magnética". Como preámbulo a la discusión subsecuente Faraday definió con toda precisión los términos que utilizaría para ello. La primera definición era la de línea de fuerza magnética como el efecto de la acción de un campo magnético sobre las líneas magnéticas, generalmente curvas y que igualmente pasan hacia,o a partir, de dipolos magnéticos o que forman círculos concéntricos alrededor de una corriente eléctrica. En seguida, Faraday define una línea de fuerza eléctrica como la fuerza ejercida a lo largo de las líneas que unen dos cuerpos, interactuando entre sí de acuerdo con los principios de inducción eléctrica (cita aquí su trabajo de 1837), y finalmente define lo que aquí nos concierne, un diamagnético, esto es, un cuerpo a través del cual pasan las líneas de fuerza magnética y bajo cuya acción no se adquiere el estado magnético usual del hierro ni de la calamita (piedra o roca imantada). Faraday fue el descubridor del fenómeno del diamagnetismo en cuanto a su diferenciación clara con el ferromagnetismo, y no sólo eso, sino que, como veremos en seguida, logró establecer de manera clara y objetiva el comportamiento diferente de la materia bajo la influencia de campos magnéticos.

Más adelante, en el trabajo ya referido, Faraday llegó a la conclusión un tanto inequívoca de que existen materiales, metales y algunas sales en particular que, bajo la acción de un campo magnético, no se comportan como imanes, y concluyó que la "condición molecular" de dichos cuerpos debía ser específicamente distinta a la del hierro magnetizado u otros similares y que por tanto "justifican una nueva condición magnética". Estos estudios lo llevaron a sospechar, y posteriormente a experimentar y probar que, con excepción de los materiales magnéticos y de sus sales, muchas otras sustancias incluyendo un vasto número de cuerpos opacos y metálicos, exhiben esta "nueva condición magnética" de la materia. Es curioso hacer notar aquí que debido a estas experiencias, Faraday consideró la posibilidad de construir una teoría general de la acción magnética basada en principios fundamentalmente simples. Este no es lugar para relatar los metódicos, cuidadosos y sistemáticos experimentos que Faraday llevó a cabo, pero en ese mismo trabajo reportaba ya que metales como el antimonio, bismuto, cadmio, cobre, oro, plomo, mercurio, plata, estaño y cinc no eran materiales ferromagnéticos, y al final anunciaba a la Royal Society de Londres que intentaría ampliar este espectro y extender sus mediciones a gases y vapores.

En una comunicación recibida el 24 de diciembre de 1845, leída el 8 de enero de 1846 y que se incluye en el trabajo ya citado, Faraday introdujo sus intenciones de ampliar sus investigaciones con las siguientes palabras:

Las características magnéticas del hierro, el níquel y el cobalto son bien conocidas, así como el hecho de que a ciertas temperaturas pierden su propiedad habitual y se transforman, ante examen y observación, en metales no magnéticos; ingresan así a la lista de materiales diamagnéticos y actúan a la par que ellos.

ñFaraday, sin saber termodinámica y mucho menos transiciones de fase, había descubierto que existe lo que hoy conocemos como una temperatura crítica y una transición de fase! Es más, continúa diciendo:

Una investigación más minuciosa me ha indicado que, aun como materiales diamagnéticos, son muy diferentes a otros cuerpos, ya que todavía calientes, siendo inactivos sobre imanes comunes o ante otras pruebas, no lo son absolutamente, ya que retienen una fracción de su potencia magnética independientemente de su temperatura...

Faraday hizo notar así, con gran claridad, que incluso entre los materiales diamagnéticos había diferencias; y continuó sus experimentos con un método y una lógica inexorables. Incluyó también vapores (gases) y el aire para finalmente anunciar, el 7 de marzo de 1850, ante la Royal Society que su trabajo sobre sustancias diamagnéticas había llegado casi a su fin y que además había sido recibido muy favorablemente en otros lugares, principalmente en Alemania[2]. Particularmente, W. Weber había manifestado su mejor deseo de confirmar tales descubrimientos. Para el 28 de noviembre de ese mismo año, el resultado era ya transparente: la palabra magnético debería emplearse para designar todos los efectos producidos por un campo de esa naturaleza, no obstante que en la subdivisión de materiales diamagnéticos fuera necesaria una diferencia entre aquellos materiales diamagnéticos per se y otros como los "imanes calientes" que retenían algunas propiedades de la magnetización —como imanes— y a los cuales, por consejo de un amigo cercano, había acordado llamar paramagnéticos. Más aún utilizó al O₂ como un caso característico de material paramagnético. Faraday sugirió el esquema:

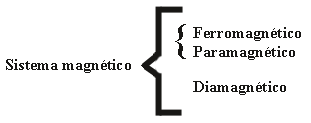
y recurrió al análisis de todo el arsenal experimental acumulado en esos años para establecer una diferenciación clara entre ellos [3].

Si se introduce un conductor paramagnético, por ejemplo una esfera de O₂ en un campo magnético originalmente en el vacío, el material provocará que las líneas de fuerza del campo se concentren sobre él y su interior, de manera que el espacio ocupado por el material transmita más energía magnética que antes (figura VIII. 1(a)). Si, por otra parte, se introduce una esfera de un material diamagnético en un campo similar, esto provocará una divergencia o separación entre las líneas en la dirección ecuatorial; por consiguiente, se transmitirá menos energía magnética en el espacio ocupado por el material que en el vacío (ñrecuérdese el efecto Meissner en superconductividad!) (figuraVIII. 1.(b)).

Figura VIII.1 (a) y (b).

De esta forma, dichos cuerpos afectan primero la dirección de las líneas de fuerza —no sólo en el espacio ocupado por ellas, sino también en el espacio cercano hacia el cual se prolongan las líneas que pasan a través de ellos—, y este cambio en el curso mismo de las líneas que los atraviesan ocurrirá, en ambos casos, en dirección opuesta. En segundo lugar, afectarán también la intensidad de la fuerza en cualquier parte del espacio dentro o cerca de ellos. El argumento subsecuente de Faraday es bien conocido pues utiliza el hecho de que la intensidad de campo en un punto depende esencialmente de la densidad de líneas de fuerza que pasa cerca de dicho punto.

Estos argumentos condujeron a Faraday a un estudio exhaustivo y profundo sobre la naturaleza de los cuerpos paramagnéticos y diamagnéticos y sus interacciones mutuas, para esclarecer el concepto de conducción magnetocristalina, de fenómenos magneto-ópticos, y de ahí Faraday llegó a la conclusión de que la atmósfera, estando formada en dos novenas partes por un compuesto altamente magnético, no estaba sujeta a grandes cambios en su carácter magnético por variaciones en la temperatura y condensación o enrarecimiento de la misma, cambios producidos por variaciones anuales y diurnas en su relación con respecto al Sol y a las fuerzas magnéticas en la superficie terrestre. Los resultados que obtuvo de este estudio metódico y exhaustivo —características indiscutibles de su trabajo— se realizaron entre 1850 y 1851. El lector interesado puede consultar el trabajo original para mayores detalles [1].

DIAMAGNETISMO

Después de los trabajos de Faraday sobre el diamagnetismo, este asunto pasó a ser un tema de rigor en el estudio de las propiedades electromagnéticas de la materia. En su bien conocido texto A Treatise on Electricity and Magnetism [4], escrito sólo unos pocos años después de la muerte de Faraday, el gran físico escocés J. C. Maxwell habla ya en términos matemáticos de este gran descubrimiento. En el capítulo sobre magnetización inducida [5] dice textualmente:

Ahora estamos preparados para considerar a la teoría del magnetismo inducido de lo que yo pude captar como el punto de vista de Faraday. Cuando una fuerza magnética actúa sobre un medio, sea magnético, diamagnético o neutral, produce en él un fenómeno de inducción magnética, una "cantidad dirigida" de la naturaleza de un flujo y, este flujo satisface las mismas condiciones de continuidad que obedecen las corrientes eléctricas y otros flujos similares.

Como es bien sabido, si es el flujo magnético, la intensidad del campo magnético, la magnetización y k la susceptibilidad magnética, las ecuaciones

= = 4p............................................(1)

= k........................................................(2)

conducen a la relación

= m,.......................................................(3)

donde m =1 + 4 pk. Para sustancias diamagnéticas k<O, como hace ver Maxwell, y m<1. Estos resultados son, hoy día, bien conocidos para cualquier estudiante de la teoría electromagnética.

Más aún, la vieja idea de Faraday de poder explicar los fenómenos eléctricos y magnéticos a partir de hechos fundamentales simples empieza a tomar cierta forma. En 1850 el físico alemán W. Weber, gran admirador del trabajo de Faraday, había lanzado la teoría de que, contrario a lo que se suponía la teoría fenomenológica de Poisson [6], las moléculas de una sustancia ferromagnética como el Fe eran pequeños imanes, aun antes de estar sujetas a la aplicación de la fuerza magnetizante y que en estos materiales el eje magnético de las moléculas gira sin diferencia en cualquier dirección, de modo que el material en su conjunto no exhibe propiedades magnéticas. Cuando una fuerza magnética actúa sobre el material, tiene el efecto de orientar los ejes de todas las moléculas en una sola dirección y provocar que el material, como un todo, se convierta en un imán.

Sin embargo, pensando en términos de corrientes moleculares, alguna diferencia debe haber entre aquellas que constituyen los materiales no diamagnéticos y los diamagnéticos. En el penúltimo capítulo de su texto [7] Maxwell analiza la forma en que Weber los diferenciaba y cómo establecía un criterio matemático para distinguirlos. Pero tocó a los físicos de este siglo elaborar una teoría satisfactoria de este fenómeno. Usando el bien conocido teorema de Larmor [8] que describe la influencia de un campo magnético sobre el movimiento de una partícula cargada, se puede demostrar [9, 10] que la magnetización inducida en un material diamagnético arroja para la susceptibilidad magnética el valor

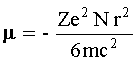..................... (4)

donde Z es el número de electrones por átomo, e la carga del electrón, N los átomos por cm³, m la masa del electrón y c la velocidad de la luz. El problema central en la ecuación 4 es el factor r², que representa el promedio del cuadrado de la distancia perpendicular del electrón al eje del campo externo. De acuerdo con la mecánica clásica, r² = 0 es el resultado del famoso teorema de Bohr-Van Leeuwen en una versión menos popular que la accesible a cualquier estudiante de mecánica estadística clásica: el fenómeno del diamagnetismo no existe, de acuerdo con las leyes de la física clásica [11].

De estos resultados se concluye que la idea de Faraday, totalmente intuitiva, de que todos los fenómenos electromagnéticos pueden obtenerse de hechos fundamentales simples no era incorrecta, pero su formulación precisa tuvo que esperar el advenimiento de la mecánica cuántica y de sus aplicaciones a sistemas formados por muchos átomos, para obtener resultados que pudiesen compararse con el experimento.

Este no es el lugar apropiado para abordar un estudio a fondo sobre la formulación del problema del diamagnetismo en el contexto de la mecánica cuántica. Hoy en día, esto es un tema obligado en los cursos avanzados de la materia y está tratado con todo detalle en los libros de texto convencionales [11-13]. El aspecto del diamagnetismo que concierne aquí es el que se conoce como diamagnetismo de Landau, en honor al físico soviético Lev Landau, quien calculó, por primera vez en 1930, cómo el diamagnetismo proviene de la cuantización de las órbitas de partículas cargadas en presencia de un campo magnético externo. Si se imagina un gas de electrones libres, despreciando al espín de los electrones contenidos en un recipiente (que por facilidad es un cubo cuyas aristas tengan longitud L) y se aplica un campo externo constante H en la dirección del eje z, resulta que los valores discretos de la energía que pueden asumir los electrones están dados por

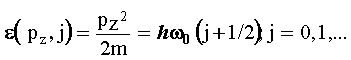.............................(5)

donde wo = eh/mc es la llamada frecuencia de ciclotrón, Pz es el valor del ímpetu del electrón en la dirección z, h=h/2p, donde h es la constante de Planck y el resto de los símbolos ya se definieron antes. Los niveles son degenerados; su grado de degeneración es igual a

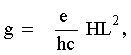.................................................................................(6)

donde gaL² refleja el hecho de que la proyección de una órbita electrónica al plano puede estar centrada en cualquier punto del mismo sin que por ello se altere su energía. Los resultados 5 y 6 permanecieron cincuenta años como una mera ilustración de que hay ciertos efectos en sistemas formados por muchas partículas que exhiben propiedades que sólo pueden ser descritas por las leyes de la mecánica cuántica y no por las de la física clásica. No obstante, esa mera ilustración dio un giro notable en 1980 y éste es el tema de la última sección del trabajo.

EL EFECTO HALL CUÁNTICO

El efecto Hall fue descubierto por el físico estadounidense E. T. Hall en 1879 [14]. Si se coloca un conductor en un campo magnético perpendicular a la dirección del flujo de la corriente eléctrica dentro del conductor, se genera en su interior un campo eléctrico a consecuencia de la desviación de las trayectorias de las partículas cargadas que produce el campo magnético. Cuando la carga eléctrica acumulada en la dirección mutuamente perpendicular a la corriente y al campo magnético llegan a un cierto valor, el campo eléctrico inducido —llamado voltaje de Hall— cancela el efecto del campo magnético, las portadoras de carga se sujetan a una fuerza neta nula y el flujo cesa. En la figura VIII.2, donde H, E_y, y V_x representan el campo magnético, el eléctrico y la velocidad de los portadores, esto tiene lugar cuando

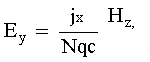. ......................................................... (7)

donde j_x = Nv_xq es la densidad de la corriente si N es el número de portadores de carga q por unidad de volumen. La cantidad

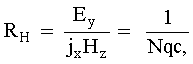................................ (8)

se conoce como la resistencia de Hall, y es negativa si los portadores son electrones. En la física de semiconductores esta cantidad tuvo un papel muy importante en la identificación de portadores de carga positivos.

Figura VIII.2

Supóngase ahora la idea un tanto estrafalaria de que se tuviera, en lugar de un metal o un semiconductor sólido, una rebanada formada por un gas de electrones libres bidimensional —esto es, cuyo espesor fuera muy pequeño comparado con sus otras dos dimensiones— y que se le aplicara un campo magnético en dirección perpendicular al flujo de electrones. La idea suena rara por la dificultad de construir físicamente en el laboratorio un sistema con dichas características. Pero si se pudiera realizar, las ecuaciones de Landau 5 y 6 podrían estar sujetas a una comprobación experimental que además corroboraría otros aspectos del viejo fenómeno del diamagnetismo. En 1980 esta alocada idea pudo ponerse en práctica, gracias a los grandes avances de la tecnología de transistores: se fabricó un sistema bidimensional de electrones libres inyectando electrones dentro de la interfase de una aleación y se pudieron confinar los electrones a una pequeña película de 500 A de espesor. El experimento que realizaron el físico alemán Klaus von Klitzing y sus colaboradores [15] arrojó un resultado verdaderamente notable, como se muestra en la figura VIII.3, y cuya explicación todavía hoy constituye un reto para los físicos teóricos.

Figura VIII.3 Resistividad de Hall y convencional.

Lo notable del resultado fue que los niveles de Landau dados en la ecuación 5, no se llenaron de electrones en la forma en que lo sugeriría el principio de exclusión de Pauli. A medida que el campo magnético aumentaba, la degeneración de los niveles también aumentaba. La máxima densidad (bidimensional) de electrones permitida por nivel para un valor dado del campo es 2 He/hc de acuerdo con la ecuación 6, tomando en cuenta el espín. Si n es esa densidad, se puede definir un "factor de llenado" como

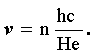................................................................ (9)

En el experimento original de von Klitzing, como se muestra en la figura VIII. 3, la resistividad de Hall muestra valores constantes para v = 1, 1/3, 2/3, etc., y con valores iguales a v^-1 en unidades de h/e². Por otra parte, la resistividad convencional (zxx en la figura) desciende a valores muy pequeños, lo que indica que en esos intervalos de valores v y H, el fluido formado por los electrones fluye como en un superconductor, casi sin resistencia. Un resultado particular se obtiene si v =1, pues de las ecuaciones 8 y 9 se sigue de inmediato que la resistividad de Hall es

R_H = h/e², ................................................................ (10)

ñuna constante universal! y que además es igual a una densidad de llenado proporcional a f_o= hc/e, un fluxón o flujo magnético cuántico elemental. Los fluxones son consecuencia directa de un efecto netamente cuántico mediante el cual un electrón extendido en el espacio puede sentir la presencia de un campo magnético confinado a una región del espacio muy lejana a la que él ocupa. Este efecto, conocido como el efecto Bohm-Aharanov fue predicho teóricamente por estos físicos en 1959 y hoy está plenamente confirmado, ha tenido fuertes y profundas repercusiones en el entendimiento del mundo cuántico [17]. El efecto von Klitzing, hoy conocido como efecto Hall cuántico, le valió el premio Nobel de física en 1985, y ha sido tan importante que la ecuación 10 se toma, hoy en día, como un patrón internacional para determinar la unidad de resistencia eléctrica. En efecto,

R_H= 25 812.8056 ohmios,

con una incertidumbre de 0.045 ppm [18].

Pero la historia no ha terminado [19]. Originalmente se pensó que en la secuencia de valores posibles para v sólo aparecían fracciones múltiplos de e²/h con denominadores impares; y hasta 1985 se habían detectado valores 1/3, 2/3, 1/5, 2/5, 2/7, 3/7, 4/9. Sin embargo, en 1987, R. Willett y sus colaboradores [19] reportaron un valor cuantizado para v= 5/2, el primero que se detectó para un denominador par [19]. Con la teoría para los casos de denominadores impares, todavía a medio camino, este nuevo efecto ha traído grandes problemas a los teóricos y hoy en día, constituye uno de los campos de investigación de mayor interés y actualidad en toda la física del estado sólido. El diamagnetismo descubierto por Faraday, claramente ejemplificado por el gas de electrones libres, plantea problemas fascinantes en un tema de la física que para muchos estaba ya agotado hace medio siglo.

REFERENCIAS

[1] M. Faraday. Experimental Researches in Electricity. Encyclopaedia Britannica, Chicago, 1978, Serie 19, p. 595.

[2] M. Faraday, op. cit., Serie 21, pp. 623 y ss.

[3] M. Faraday, op. cit., Serie 26, pp. 688-727.

[4] J.C., Maxwell, A Treatise on Electricity and Magnetism. Dover, Nueva York, 1945, vol. II, cap. IV.

[5] J.C. Maxwell, op. cit., cap. IV, p. 55.

[6] J.C. Maxwell, op. cit., cap. IV, p. 57.

[7] J.C. Maxwell. pp. cit. cap. XXII, p. 475.

[8] H. Goldstein. Classical Mechanics. Addison-Wesley, Cambridge, Mass., 1953, pp.176-178.

[9] C. Kittel. Introduction to Solid State Physics. 3a. ed. John Willey & Sons, 1967.

[10] R. Becker y F. Sauter. Electromagnetic Fields and Interactions. Blaisdell, Nueva York, 1964, cap. C-III.

[11] R. Kubo, H. Ichimura, T. Usui y N. Hashizumi. Statistical chanics. North Holland, Amsterdam, 1965, p. 138.

[12] R. K. Pathria. Statistical mechanics. Pergamon Press, Oxford, 1972.

[13] K. Huang. Statistical Mechanics. 2a. ed. John Willey & Sons, Nueva York, 1987.

[14] R. Resnick y D. Halliday. Physics. Part. II 3a. ed. John Willey & Sons, Nueva York, 1978, secs. 33-35.

[15] K. von Klitzing. Rev. Mod. Phys., vol. 53, núm. 3, 1986, pp. 519-532.

[16] D. Bohm y Y. Aharanov. Physical Review, vol. 115, 1959, p. 485; véase también K Huang. op. cit.

[17] Y. Imry y R. A. Webb. Scientific American, vol. 260, núm. 4, 1989, p.36.

[18] E. Richard Cohen y B. N. Taylor. Physics Today. vol. 44, núm. 8, parte 2, 1991, p. BG9.

[19] Véase Physics Today, vol. 44, núm. 1, 1988, pp. 17-20 y las referencias ahí citadas.