XVI. LA TURBULENCIA DE LOS FLUIDOS

EL FENÓMENO de la turbulencia ha sido estudiado por un buen número de científicos a lo largo de más de 150 años. Desafortunadamente durante casi todo este tiempo no se le pudo dar una explicación satisfactoria. No fue sino hasta el decenio 1980-1990 que finalmente se ha empezado a entender el fenómeno de la turbulencia en términos de caos.

Cuando el agua de un río fluye por su cauce sabemos que existen diferentes formas de flujo. Si la velocidad del agua es pequeña, entonces este flujo es regular; cuando el agua pasa por alguna piedra que está en el río, simplemente la rodea y el flujo continúa de manera regular. Se dice que el flujo es laminar, ya que su movimiento ocurre como si un conjunto de láminas de agua fluyera una sobre otra.

Sin embargo, al aumentar la velocidad del agua llega cierto momento en que el flujo se vuelve altamente irregular. Nos damos cuenta de que al bordear la piedra se producen remolinos. Si la velocidad del agua es mucho más alta todavía, aparecen remolinos dentro de los remolinos. En estas condiciones el flujo del agua es turbulento.

La descripción inicial de estos fenómenos, que corresponden a la hidrodinámica, fue hecha aplicando las leyes del movimiento de Newton a los fluidos. De esta manera se encontró una ecuación que resultó ser no lineal. En la bibliografía técnica esta ecuación recibe el nombre de Navier-Stokes. Como ha ocurrido con la mayoría de las ecuaciones no lineales, la ecuación de Navier-Stokes no se ha podido resolver de manera exacta.

En el caso en que la velocidad del líquido es muy reducida, el término no lineal de la ecuación de Navier-Stokes resulta ser extraordinariamente pequeño y es posible no tomarlo en cuenta, obteniéndose así una ecuación lineal, que sí se ha podido resolver. Bajo estas condiciones nos encontramos en el régimen laminar. Las propiedades de los flujos laminares se han obtenido y se conocen bastante bien. De hecho, gran parte de la tecnología basada en la hidrodinámica se ha desarrollado a partir de las soluciones de la ecuación de Navier-Stokes linealizada.

Un ejemplo de turbulencia ocurre cuando se calienta un pocillo de agua en una estufa. Como se sabe, si se deja calentar el agua un tiempo suficiente, ésta aumenta su temperatura y empieza a verse un movimiento en el agua, que recibe el nombre de convección. La causa de la convección se debe a que la porción de agua más cercana a la flama se calienta y por tanto su volumen aumenta. Al ocurrir esta dilatación, esta agua se vuelve más ligera que el agua más fría de arriba. Por tanto, el agua fría es más pesada y se mueve hacia abajo, desalojando a la caliente, que a su vez se mueve hacia arriba. De esta forma se genera un movimiento tipo circular de abajo hacia arriba y de arriba hacia abajo.

A medida que continúa aumentando la temperatura, el movimiento se hace muy irregular y, cuando esto sucede, se dice que ha empezado la turbulencia.

En la década de 1980-1990 se hicieron varios trabajos muy cuidadosos sobre la turbulencia debida a variaciones de la temperatura. Para estudiar este fenómeno se encierra un líquido en una cápsula muy pequeña y se mantiene una diferencia de temperatura fija entre las superficies superior e inferior de la cápsula. La superficie inferior se mantiene más caliente que la superior. Esta diferencia de temperatura causa que el líquido en la parte inferior se expanda, volviéndose más ligero que el de arriba. Éste empieza a bajar y el de abajo sube, es decir, ocurre la convección. Si las longitudes del recipiente tienen valores bien determinados, el movimiento del líquido se realiza alrededor de trayectorias cilíndricas (figura 34).

Después de cierto tiempo, si no cambia la diferencia de temperatura entre ambas caras, el movimiento se hace estacionario, lo que quiere decir que el giro se vuelve periódico; el líquido tarda cierto tiempo en dar una vuelta completa. En el experimento se mide este tiempo o periodo de flujo.

El experimento se lleva a cabo cambiando gradualmente la diferencia de temperaturas entre las caras de la cápsula. Para cada valor de esta diferencia se espera el tiempo necesario hasta que se llega a una situación estacionaria y se registra el periodo del movimiento.

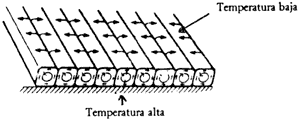
Figura 34. En determinadas circunstancias el movimiento de convección se da en trayectorias cilíndricas.

Lo que se encontró es que al aumentar la diferencia de temperaturas llega un momento en que aparecen dos periodos, es decir, hay dos tiempos de giro, y no nada más esto, sino que uno de los tiempos es igual al que había anteriormente, y el otro tiene valor doble respecto al primero. Esto significa que se presenta un fenómeno de bifurcación (véase el capítulo VIII).

Al seguir aumentando la diferencia de temperatura llega otro momento en que parecen cuatro tiempos, o sea cuatro periodos, es decir, se produce otra bifurcación. Continuando de esta manera se encuentran las características que estudiamos en el capítulo VIII, sobre el camino al caos. Hemos de decir que en este caso particular la diferencia de temperatura entre las caras de la cápsula es el análogo de la cantidad q con la que se trabajó en la ecuación (6) del capítulo VIII. Una mayor diferencia de temperatura corresponde a un valor mayor de este parámetro.

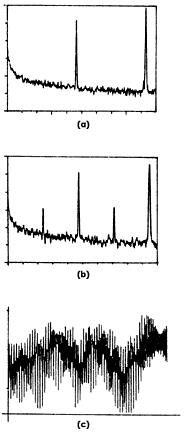
Figura 35. Frecuencias características que aparecen al aumentar continuamente la diferencia de temperaturas: (a) hay dos frecuencias; (b) hay cuatro frecuencias, y (c) Caso en que hay turbulencia. Las frecuencias son muchísimas. Se ha llegado al régimen caótico.

Una forma —que resultó adecuada— de presentar los resultados fue haciendo un análisis no de periodos sino de frecuencias. En la figura 35 se muestra una sucesión de las frecuencias que aparecen para cada valor fijo de la diferencia de temperatura, o sea, del valor q. En primer lugar, cuando el valor de la diferencia es suficientemente pequeño, sólo hay una frecuencia (o sea, un solo periodo); al aumentar esta diferencia, llega un momento en que aparecen dos frecuencias (figura 35 (a)), una igual a la anterior y la otra igual a la mitad. Al aumentar todavía más la diferencia de temperatura aparecen cuatro frecuencias, la inicial, una igual a la mitad, otra de valor igual a la cuarta parte y otra más igual a la octava parte del valor de la inicial (figura 35(b)). Si la diferencia de temperatura continúa aumentando, van apareciendo más y más frecuencias precisamente con los valores asociados con las bifurcaciones. Finalmente, llega un momento en que hay frecuencias de todos los valores (figura 35(c)). Se ha llegado al régimen caótico. En esta situación, dentro del fluido se inicia el régimen turbulento. Por tanto, se ha demostrado que la turbulencia está asociada precisamente al caos que describirnos en el capítulo VIII.

Se han realizado diversos experimentos análogos, con condiciones que generan turbulencias. Los análisis de los resultados obtenidos, bajo el punto de vista que acabamos de considerar, indican que al iniciarse la turbulencia es cuando empieza el caos. La relación entre turbulencia y caos en un fluido es tema de investigación activa en la actualidad.