XX. SEGURIDAD Y CAT�STROFE

EL COMPORTAMIENTO de un sistema complejo, al que en general rigen leyes no lineales, puede entenderse, como vimos, en t�rminos de regiones peri�dicas y de regiones ca�ticas. En el cap�tulo VIII estas regiones quedan delimitadas por valores precisos de los par�metros caracter�sticos del sistema. En el ejemplo tratado en el cap�tulo VIII, el sistema est� representado por un solo par�metro, q. En la figura 19 podr�amos colorear los valores de q que dan lugar a un comportamiento peri�dico con un color, rojo, por ejemplo, y con otro, azul digamos, los valores de q que dan un comportamiento ca�tico.

Sin embargo, en muchos sistemas no es uno sino varios los par�metros que lo conforman. En este caso, el comportamiento es similar al que estudiamos, pero hay una diferencia. El hecho de que haya varios par�metros hace que la frontera entre un tipo de comportamiento, peri�dico, y otro, ca�tico, no sea tan f�cil de definir. Para aclarar lo que ocurre, supongamos que un sistema est� regido por una ecuaci�n no lineal, similar a la ecuaci�n (6) del cap�tulo VIII,que tenga dos par�metros, que llamaremos p y r. Procediendo de manera an�loga a corno se hizo en el cap�tulo VIII, dados valores espec�ficos de p y r, por ejemplo p 2.1 y r = 0.43, se obtendr�a el tipo de comportamiento que sigue este sistema. Si se cambian los valores p y r (equivalente a cambiar el valor de q) se vuelve a encontrar el tipo de comportamiento, y as� se contin�a para todas las posibilidades de p y de r.

Podemos presentar los resultados de este procedimiento de la forma siguiente: consideremos dos ejes perpendiculares (figura 41) en los que uno de los ejes, el horizontal, marque los valores de p, y el vertical los de r. Para un conjunto de valores de p y de r dados (en la figura, para el valor p = a y r = b) marcamos el punto P. Ahora bien, si este par de valores de los par�metros da como resultado un comportamiento peri�dico del sistema, entonces el punto P lo marcamos de negro, por ejemplo. Si el comportamiento del sistema para esta pareja de valores resulta ser ca�tico, entonces marcamos el punto P con otro tono, blanco, por ejemplo. De esta manera se obtiene una figura corno la de la figura 42. Observamos que las regiones blancas y negras est�n entremezcladas.

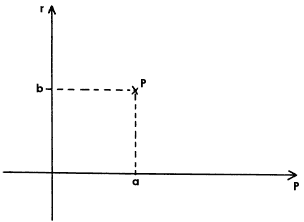
Figura 41: Gr�fica para el caso en que haya dos par�metros que describan el sistema.

Si quisi�ramos ver en detalle la frontera entre una regi�n negra y una blanca adyacente, esto es, si amplific�ramos la regi�n encerrada en la figura 42, obtendr�amos lo que se ve en el figura 43; si ahora amplific�ramos cualquier regi�n de la figura 43, se encontrar�a una figura similar a la figura 43.

Continuando de esta manera, al ir yendo a escalas cada vez m�s peque�as se muestra la gran complejidad de la separaci�n entre dos regiones adyacentes, la negra y la blanca. De hecho, se puede uno dar cuenta de que al cambiar de escala hay similitud en las figuras que se van obteniendo. Por tanto, estas figuras son fractales.

Si el sistema estuviera regido por m�s de dos par�metros, la representaci�n de lo que ocurre ya no la podr�amos hacer en dos dimensiones, sino en un n�mero mayor, cosa que no haremos.

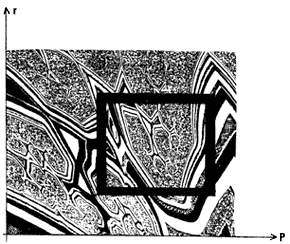
Figura 42. Las regiones negras corresponden a valores de los par�metros para los cuales hay un comportamiento estable. Las regiones blancas corresponden a comportamientos ca�ticos.

Figura 43. Amplificaci�n de la zona encerrada en la figura 42.

Consideremos como ejemplo de un sistema complejo la red el�ctrica de una regi�n del pa�s. Este sistema es oscilatorio y un gran problema es saber lo que le ocurre si por alg�n motivo se presenta una perturbaci�n, como puede ser alguna variaci�n en el voltaje o la falla de una parte del sistema.

Cuando el sistema est� funcionando en forma estable, los valores de los par�metros tendr�n ciertos valores a los que corresponder� un punto en una regi�n como la negra de la figura 42, que llamamos Q. Si ocurre alguna perturbaci�n en la red, entonces los valores de los par�metros cambian y por tanto el punto Q ya no describe al sistema perturbado, sino que ser� otro punto el que lo represente, digamos el T. Si �ste cae dentro de una regi�n negra, entonces bajo los efectos de la perturbaci�n, el sistema seguir� funcionando de forma peri�dica, ser� estable. Pero �qu� ocurre si el punto T cae en una regi�n blanca? En este caso el comportamiento del sistema ser� ca�tico y habr� problemas.

Si el comportamiento del sistema est� representado por gr�ficas an�logas a las de las figuras 42 y 43, entonces una peque�a variaci�n en los par�metros p y r puede pasar al sistema de una regi�n negra (estable) a otra blanca (ca�tica), que est� en su vecindad. N�tese que los puntos de una regi�n negra est�n muy cercanos, de hecho entremezclados, a los de las regiones blancas.

En general, el dominio en el cual un sistema complejo se comporta de manera estable se adivina a partir de un conjunto peque�o de datos. En el funcionamiento cotidiano de estos sistemas, el comportamiento se extrapola de modo que cubra una variaci�n muy estrecha de valores de los par�metros. Sin embargo, esta extrapolaci�n no est� completamente justificada. �Qu� ocurre si al extrapolar se pasa de una regi�n negra (estable) a una blanca (ca�tica)? N�tese que una peque�a variaci�n puede cambiar completamente el comportamiento del sistema.

Un problema que debe tratarse al considerar el dise�o de un sistema no lineal, como la red el�ctrica, es poder conocer con detalle la frontera entre las regiones estables (negra) y ca�tica (blanca), la frontera entre la calma y la cat�strofe. Dentro de los sistemas conocidos esta frontera todav�a no se conoce con exactitud. Este problema es abierto. Es claro que, una vez conocida esta frontera, se podr� saber a ciencia cierta cu�ndo los comportamientos ser�n seguros y se podr�n tomar las providencias necesarias para evitar caer en una regi�n ca�tica.