XIX. EL DISEÑO DE ESTRUCTURA EN LA INGENIERĶA
VAMOS a construir un fractal de la siguiente forma. Tomemos una
línea recta de cierta longitud (figura 36(a)) que supondremos que es de valor
uno. Dividamos ahora esta línea en tres partes iguales y quitemos la parte central
(figura 36(b)). Cada segmento de los que quedaron tiene ahora longitud igual
a (1/3).
Enseguida repetimos el mismo procedimiento con cada uno de los segmentos restantes, obteniendo la figura 36(c). Cada uno de los segmentos tiene una longitud de (1/9) (un tercio de un tercio). Por tanto ahora se tienen cuatro segmentos de longitud (1/9) cada uno.
Si se repite este procedimiento con cada uno de los segmentos obtenidos, se encuentran sucesivamente las líneas mostradas en la figura 36 (d). En cada paso se va encontrando un número mayor de segmentos, pero cada uno de menor longitud.
Si se llevara a cabo este procedimiento un número muy grande de veces, se llegaría
a obtener un "polvo" formado de un número extraordinariamente grande de segmentos,
cada uno de longitud pequeñísima.
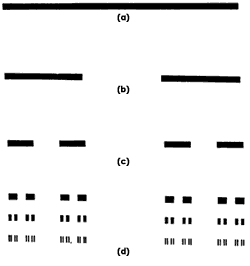
Figura 36. Procedimiento para construir el polvo de Cantor.
Supongamos que la longitud de la línea original, la de la figura 36(a) es igual a 1. La longitud de cada línea de la figura 36(b) es entonces igual a (1/3). Por tanto, como hay dos líneas, la longitud total de las líneas de la figura 36(b) es:
En la figura 36(c) hay 4 líneas y cada una tiene de longitud:
Por tanto, la longitud total de las líneas de la figura 36(c) es:
En el primer renglón de la figura 36(d) hay ocho líneas y cada una con una longitud igual a:
En consecuencia, la longitud total de las líneas de este renglón es:
Continuando de la misma manera vemos que en el segundo renglón de la figura 36(d) hay 16 líneas, cada una con una longitud de:
En el tercer renglón de la figura 36(d) hay 32 líneas, cada una tiene de longitud:
En resumen, vemos que las longitudes totales de las líneas de las figuras 36(d) son, sucesivamente:
Cada vez que pasamos de una figura a otra la longitud total va disminuyendo, pero el número de líneas va aumentando (de l a 2 a 4 a 8 a l6 a 32 a ...).
Si así continuáramos indefinidamente, el número de líneas crecería sin límite y la longitud total sería cada vez más y más pequeña.
Este conjunto de segmentos se denomina el polvo de Cantor. Ahora comparemos
los segmentos en el primer y segundo renglones de la figura 36(d). Nos damos
cuenta de que ambas figuras son similares; lo mismo sucede al comparar el segundo
y el tercer renglones. Esto nos indica que el polvo de Cantor es un fractal,
con una dimensión de 0.63, que es un número comprendido entre 0 y 1. Esta dimensión
es mayor que 0, ya que el polvo es mucho más que un punto (dimensión 0) y mucho
menos que una línea continua (dimensión 1).
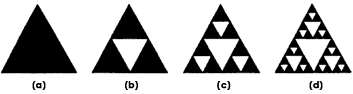
Figura 37. Procedimiento para construir una empaquetadura de Sierpinski.
Uno se puede preguntar si es posible construir un fractal análogo al polvo de Cantor, pero en lugar de que sea en una dimensión, que ocurra en dos dimensiones. La respuesta es positiva.
Tomemos como base un triángulo con los tres lados iguales, o sea equilátero (figura 37(a)). Enseguida dividimos cada lado en dos partes iguales y construimos otros tres triángulos idénticos al anterior y los unimos como se muestra en la figura 37(b), dejando en blanco la porción central, que tiene la forma del mismo triángulo con el que iniciamos la construcción. Enseguida eliminamos el triángulo central.
En el siguiente paso dividimos cada lado de cada triángulo en dos partes iguales y formarnos los triángulos mostrados en la figura 37(c). Asimismo quitamos los triángulos blancos.
Continuando de esta manera se llega a configurar un objeto como el mostrado en la figura 37(d). Si se sigue así indefinidamente se construirá un objeto que recibe el nombre de empaquetadura (gasket en inglés) de Sierpinski. Nos damos cuenta de que este objeto tiene agujeros en todas las escalas, y que es autosimilar, por lo que es un fractal. La dimensión fractal que tiene la empaquetadura de Sierpinski es 1.58. Nótese que esta figura es más que una línea recta (dimensión 1) y menos que una superficie (dimensión 2).
Supongamos que la longitud del lado del triángulo de la figura 37 (a) sea igual a 1. El perímetro de este triángulo es igual a la suma de sus tres lados, o sea:
La longitud de cada línea de la figura 37(b) es (1/2) Por tanto, cada triángulo negro tiene un perímetro de:
En vista de que hay tres triángulos negros, su perímetro total es:
La longitud de cada línea de la figura 37(c) es:
Cada triángulo negro de esta figura tiene un perímetro de:
En vista de que hay nueve triángulos negros, su perímetro total es:
En la figura 37(d), la longitud de cada línea es:
En consecuencia, cada triángulo negro tiene un perímetro de:
Dado que hay 27 triángulos negros, su perímetro es:
De estos cálculos apreciamos que al pasar de una figura a la siguiente, el perímetro de los triángulos negros va aumentando: 3, 4.5, 6.75, 10.125, ... Sin embargo, también vemos que de una figura a la otra, el número de huecos también aumenta, por lo que el área total de los triángulos negros va disminuyendo. Si se siguiera este procedimiento indefinidamente, concluiríamos que la empaquetadura de Sierpinski ¡tiene un perimetro infinito pero su área es de cero!
Se puede, asimismo, iniciar la construcción en dos dimensiones con un cuadrado, en lugar de iniciarla con un triángulo. Al cuadrado se le quita al centro un cuadrado de lado igual a (1/3) del lado original. En seguida se remueven los centros de los ocho cuadrados que quedan y así se continúa.
También se puede construir el análogo en tres dimensiones (figura 38). Su construcción se inicia con un tetraedro regular (pirámide cuyas caras son cuatro triángulos equiláteros). Unimos cuatro pirámides de modo que en el interior quede en blanco una pirámide igual a ellas; ésta se elimina. Continuando de esta manera se obtiene la versión tridimensional de la empaquetadura de Sierpinski. La dimensión de esta construcción es igual a 2, que es menor que 3 en la cual se construyo. Resulta claro, ya que la generalización tridimensional no llena completamente el espacio. Este objeto, llamado esponja de Menger tiene ¡área superficial infinita y volumen nulo!
Nos damos cuenta de que las construcciones de Cantor, Sierpinski y Menger son
objetos muy calados, que tienen longitud (Cantor), área (Sierpinski) y volumen
(Menger) prácticamente nulos, ya que en el límite infinito casi no existen ni
segmento, ni triángulo, ni pirámide, respectivamente. Desde este punto de vista
matemático, tales construcciones son patológicas.

Supongamos que la masa del triángulo de la figura 37(a) es igual a 1. Cada triángulo de la figura 37(b) tiene entonces una masa igual a (1/4). Como solamente quedan tres de estos triángulos, la masa total en le figura 37(b) es:
La masa de cada triángulo negro de la figura 37(c) es la cuarta parte de la de un triángulo negro de la figura 37(b). Como la masa de este último triángulo es (1/4), la masa de cada triángulo negro de la figura 37(c) es:
Dado que en la figura 37(c) hay nueve triángulos negros, cada uno de masa igual a (1/16), la masa total en esta figura es:
La masa de cada triángulo negro de la figura 37(d) es la cuarta parte de la de un triángulo negro de la figura 37(c). En vista de que la masa de este último triángulo es igual a (1/16), la masa de cada triángulo negro de la figura 37(d) es:
En la figura 37(d) hay 27 triángulos negros y cada uno de ellos tiene una masa de (1/64). Dado que hay 27 de estos triángulos, en la figura 37(d) hay una masa de:
Ahora bien, vemos que los triángulos de cada una de las figuras incluidas en
la figura 37 están dentro del área del triángulo original (figura 37(a)). Por
tanto, la sucesión de triángulos de la figura 37 va teniendo cada vez menos
y menos masa (1, 0.75, 0.5625, 0.4219, ...) y éstas están encerradas en la misma
área. En consecuencia, la sucesión de figuras que da lugar a la empaquetadura
de Sierpinski se va volviendo cada vez más y más ligera. En el límite en que
el número de pasos es extraordinariamente grande, el número de triángulos es
también muy grande pero la masa total encerrada es muy pequeña, ¡casi nula!
La empaquetadura de Sierpinski es notablemente ligera.
Figura 39. El punto R se llama ramal.
Otra característica importante de esta construcción es la siguiente. Consideremos una curva como la que se muestra en la figura 39; al punto R se le llama punto ramal. De acuerdo con el "sentido común" uno podría pensar que una curva no puede consistir solamente de puntos ramales. Sin embargo, si consideramos el perímetro, o sea, la línea que encierra la empaquetadura de Sierpinski, ésta es una línea formada solamente por puntos ramales. Es decir, en cada punto sale un ramal de la curva. Por supuesto, esto ocurre en el caso en que se ha iterado un número muy grande de veces.
Las empaquetaduras de Sierpinski, tanto en dos como en tres dimensiones, son
modelos de muchas estructuras construidas por el hombre, así como de varios
fenómenos naturales. Un caso interesante se dio en la ingeniería civil, cuando
Gustave Eiffel construyó su famosa torre en París, Francia, en 1889 (figura
40). Esta construcción de 335 m de altura tiene cuatro lados y cada lado tiene
la forma de una letra A. Los cuerpos de cada parte de la A no están construidos
con vigas sólidas, llenas, sino con armaduras gigantescas. Si uno se fija con
detalle en cada una de estas armaduras, se dará cuenta de que están formadas,
a su vez, de otras armaduras, que están formadas de armaduras, que a su vez
son armaduras, que a su vez... Así se obtiene una estructura autosimilar que
constituye un fractal. Si compararnos una armadura y una viga cilíndrica llena
con la misma capacidad de carga, la armadura resultará muchísimo más ligera
que la viga. Eiffel sabía que las armaduras, cuyos miembros las integran a su
vez armaduras, son todavía más ligeras. Así, vemos que la Torre Eiffel es una
aproximación a la empaquetadura de Sierpinski en tres dimensiones. Además, se
trata de una estructura muy ligera, igual que en el caso de Sierpinski.

Figura 40. La estructura de la Torre Eiffel se acerca a una esponja de Menger.
Otro punto importante y crucial con respecto a la capacidad de carga de una estructura es que, mientras más puntos ramales tenga una estructura, mayor será la resistencia que pueda soportar. Resulta que la Torre Eiffel cuenta con muchos puntos ramales. El famoso arquitecto estadunidense Buckminster Fuller, diseñador de los domos geodésicos muy populares en la década 1960-1970, sabía que la capacidad de carga reside no en la masa total de la estructura sino en los puntos ramales que tenga. Mientras más puntos ramales tenga una estructura más se acercará al ideal de una empaquetadura de Sierpinski y mayor será la carga que pueda soportar.
De esta forma se pueden lograr estructuras muy ligeras que son capaces de soportar cargas muy grandes. Mientras más se acerquen a una empaquetadura de Sierpinski o a una esponja de Menger, mejor se logrará este efecto.