XXV. LOS ASTEROIDES

ENTRE Marte y Júpiter se localiza un cinturón de asteroides, integrado por rocas de dimensiones diversas y que giran alrededor del Sol. Quizá los componentes de un planeta que no llegó a formarse. El tamaño de estas rocas es mucho menor que el de cualquiera de los planetas conocidos: un ejemplo es Gaspra, fotografiado en 1991 por la nave Galileo a una distancia de 5 300 km; mide 19 por 12 por 11 kilómetros.

Se considera que el cinturón de asteroides contiene varios millones de cuerpos y se podría pensar que en el espacio que ocupa las rocas chocan continuamente entre sí. Sin embargo, el volumen del cinturón es tan grande que la distancia común entre dos asteroides es de varios millones de kilómetros, por lo que los acercamientos y las colisiones entre ellos son muy raros.

Debido a que el tamaño de los asteroides es mínimo en comparación con el de los planetas vecinos, cada uno de ellos es, de hecho, una sonda que casi no ejerce fuerza alguna sobre aquéllos pero que sí experimenta sus efectos. Por eso son de interés para el presente estudio pues cosas extrañas ocurren en los asteroides. Cada uno de ellos está sujeto, además de la fuerza atractiva del Sol, a las ejercidas por Marte y Júpiter, lo que causa que su trayectoria alrededor del Sol sea ondulada. Se podría uno preguntar si, a lo largo de tiempos muy grandes, tales perturbaciones, que son relativamente pequeñas, se pudieran acumular y causar cambios radicales en sus órbitas.

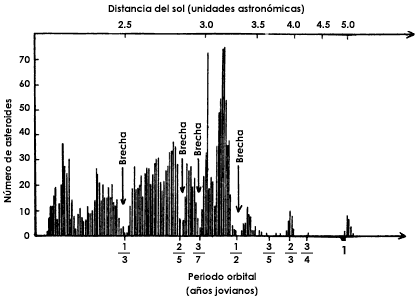
Figura 48. Gráfica del número de asteroides a distintas distancias del Sol.

A mediados del siglo pasado se empezó a estudiar la trayectoria de varios asteroides y se descubrió un hecho interesante. Al medir su distancia al Sol se encontró que había algunas para las cuales prácticamente no había asteroides. Con más detalle, si se hace una gráfica en la que se enumere la cantidad de asteroides situada a cada distancia (figura 48) se encuentra que a ciertas distancias del Sol casi no hay asteroides sino brechas. En la gráfica se ha usado como unidad de distancia la unidad astronómica (abreviada u.a.), que equivalee a la distancia del Sol a la Tierra, unos 150 000 000 km. Así, por ejemplo, a las distancias de aproximadamente 2.5 u.a., 2.8 u.a., 2.9 u.a., 3.3 u. a., no hay asteroides.

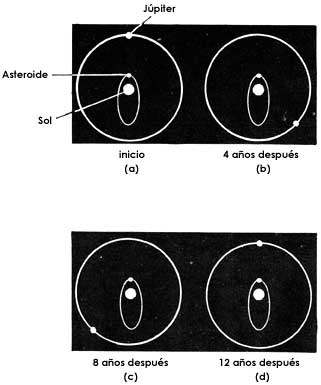
Figura 49. Movimiento de un asteroide que tiene con Júpiter una resonancia de 3:1.

Ahora bien, como se vio en el capítulo anterior, la tercera ley de Kepler nos indica que hay una relación entre la distancia de un cuerpo al Sol y el tiempo en que completa su órbita, esto es, su año, o su periodo orbital. Por tanto, también se puede contar el número de asterorides que tienen determinado periodo orbital. En este caso conviene tomar como unidad el año de Júpiter (aproximadamente 4 333 días, el año joviano). La escala de tiempos se muestra en la misma figura 48. De ésta vemos que a la distañcia de 2.5 u. a., a la que le corresponde un periodo orbital de (1/3) que es igual a 1444 días, casi no hay asteroides. De la misma gráfica vemos que tampoco hay gran número de asteroides en los periodos orbitales de (2/5) (2.8 u. a.), (3/7) (2.9 u. a.), (1/2) (3.3 u a) de años jovianos, etcétera.

Lo curioso de este descubrimiento es que, como se ve, las brechas se dan en periodos que son cocientes de números enteros: el periodo de (1/3) es el cociente de 1 entre 3; el periodo de (2/7) es el cociente de 2 entre 7, etc. A estos periodos se les llama resonancias; a (1/3) se le llama la resonancia de 3:1; a (2/7), la resonancia de 7:2, y así sucesivamente.

La figura 49 muestra lo que ocurre a un asteroide cuyo periodo se halla en la resonancia 3:1 con Júpiter. En la figura (a) el planeta y el asteroide están a la mínima distancia. En (b), (c) y (d) vemos las posiciones de Júpiter después de cada vuelta completa del asteroide. Después de 12 años estos cuerpos volverán a estar nuevamente a la mínima distancia (figura 49(d)). Queda claro que el asteroide y el planeta se acercan casi a las mismas posiciones en intervalos regulares. Al transcurrir el tiempo, durante millones de años, estas coincidencias acumulan efectos que pueden ser perceptibles y que podrían modificar el tamaño de la órbita del asteroide. La cuestión que se planteó fue si estas resonancias podrían causar inestabilidades en las órbitas de los asteroides que estan en resonancia y que, en consecuencia, sus órbitas aumentaran tanto que tomaran una nueva órbita en la que no hubiera ninguna resonancia. Quedaría claro entonces que si alguna vez hubo algún asteroide en resonancia, después de mucho tiempo habría cambiado de órbita y la población de asteroides en resonancia disminuiría.

Desde el siglo pasado se trató de resolver esta cuestión buscando soluciones a las ecuaciones de Newton ajustadas al sistema asteroide, Marte y Júpiter. Sin embargo, por el motivo que se mencionó en el capítulo anterior, sólo se pudo hacer entonces para intervalos de tiempo muy pequeños, alrededor de 10 000 años, con el resultado de que en estos intervalos de tiempo no ocurría ninguna modificación de la órbita del asteroide.

No fue sino hasta la década 1970-1980 que, disponiéndose ya de computadoras electrónicas, fue posible hacer cálculos que cubrieran intervalos de tiempo mucho mayores. Se supuso que se colocaban 300 asteroides a las distancias correspondientes a la resonancia 3:1. Cada uno con diferente posición y velocidad. Las diferencias entre estas condiciones iniciales eran tales que diversos asteroides tenían posiciones iniciales distintas. Se inició el cálculo de las órbitas que seguiría cada uno de estos objetos durante dos millones de años y se halló que, para ciertas condiciones iniciales, las órbitas que seguían los asteroides no cambiaron de tamaño en dos millones de años. Es decir, estas condiciones daban lugar a órbitas estables. Además, se descubrió que para otro tipo de condiciones iniciales, en ciertos instantes las órbitas cambiaban abruptamente su tamaño. Estas condiciones iniciales corresponden a regiones caóticas.

En la figura 50 se muestra la gráfica del tamaño de la órbita de un asteroide de la región caótica en la resonancia 3:1, con el transcurso del tiempo. Podemos apreciar que, en los instantes marcados por las flechas, el tamaño de la órbita crece desmesuradamente. Se ve que un asteroide puede permanecer alrededor de 150 000 años en una órbita reducida y de pronto cambiarla notablemente. La nueva órbita es tan grande que, al recorrerla, el asteroide cruza las órbitas de Marte y la Tierra. Con el tiempo, puede ocurrir que el asteroide y uno de estos dos planetas choquen. De esta manera, los asteroides cuyas órbitas caen inicialmente en la zona caótica de la resonancia 3:1, gradualmente van desapareciendo creándose así la brecha en el cinturón.

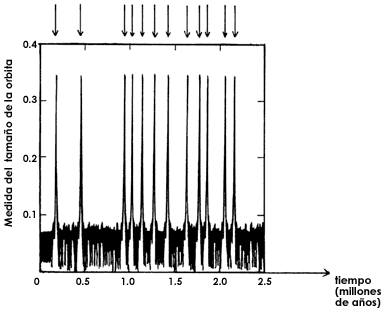
Figura 50. Variación en el tiempo de los tamaños de las órbitas de asteroides en la zona caótica.

Lo anterior también explica el hecho de que sobre la Tierra han caído meteoritos cuya composición química es parecida a la de los del cinturón de asteroides. Hasta épocas recientes no se había podido explicar cómo éstos podrían llegar hasta nuestro planeta. Por tanto, se puede pensar que la zona del cinturón de asteroides, con distancias que corresponden a la resonancia 3:1, es la fuente de algunos de los numerosos meteoritos caídos en nuestro planeta.

En la misma figura 50 vemos que si el asteroide no experimenta ninguna colisión, después de cierto tiempo vuelve a alterarse el tamaño de su órbita y cambia a otra órbita de tamaño parecido al que tenía originalmente. Al seguir transcurriendo el tiempo vuelve a recorrer una órbita muy grande. Posteriormente cambia a una pequeña y así sucesivamente.

Lo interesante de este descubrimiento es saber que en ciertas circunstancias y con determinadas condiciones iniciales el comportamiento de un cuerpo del Sistema Solar puede ser caótico. Esto es lo que había intuido Poincaré a principios de siglo sin haberlo podido demostrar. Las ecuaciones de Newton incluyen este tipo de dinámica.