AP�NDICES
AP�NDICE A. DERIVACI�N DE LA DISTANCIA AL SOL HECHA POR ARISTARCO
Con el fin de hacer m�s inteligible el m�todo utilizado por Aristarco en su determinaci�n de la distancia al Sol, hemos introducido la notaci�n algebraica y trigonom�trica moderna, lo que no cambia la esencia de ese c�lculo geom�trico.
En el tri�ngulo de la figura 7, S representa la posici�n del Sol, T
la de la Tierra y L la de la Luna en el momento de su cuadratura. En
esa misma figura la distancia entre la Tierra y el Sol es el segmento 
.
La que nos separa de nuestro sat�lite es el segmento 
y la que hay entre la Luna y el Sol es el segmento 
.
El �ngulo que se desea conocer con gran precisi�n es el a.
En el instante mismo de la cuadratura lunar se cumple rigurosamente que el �ngulo b = 90°. Bajo esa condici�n Aristarco midi� el valor del �ngulo a, encontrando que era igual a 87.lcirc.
Como la configuraci�n de los tres cuerpos celestes es la de un tri�ngulo, se puede aplicar la relaci�n trigonom�trica que establece que la suma de los tres �ngulos interiores de cualquier tri�ngulo es igual a 180°. En el caso que nos ocupa se tendr� que
Como a= 87.1° y b = 90°, entonces resulta que g = 2.9°.
Una vez que se ha determinado el valor del �ngulo g, puede aplicarse la relaci�n trigonom�trica conocida como la ley de los senos, la cual establece que en todo tri�ngulo sus lados son proporcionales a los senos de los �ngulos opuestos. Para el tri�ngulo que analiz� Aristarco esta ley se puede escribir de la siguiente forma:
![[FNT 85]](../img/155_268a.gif){kind=small}
Como lo que interesa es conocer el valor del segmento TS, basta despejarlo algebraicamente de esta �ltima relaci�n y sustituir los valores de los senos de los �ngulos involucrados, as� se obtiene que:
![[FNT 86]](../img/155_268b.gif)
Los valores de sen(90°) y sen(2.9°) son conocidos. Se pueden obtener mediante una calculadora electr�nica de bolsillo o en las tablas de funciones trigonom�tricas de uso com�n en las escuelas de ense�anza media. Aristarco conoc�a esos valores pues dispon�a de relaciones geom�tricas aplicables a los tri�ngulos.
Como el sen(90°) = 1.0000 y el sen(2.9°) = 0.0505, se tendr� que
![[FNT 87]](../img/155_268c.gif)
De esta manera Aristarco encontr� que la distancia que nos separa del Sol es alrededor de 20 veces mayor que la que nos separa de la Luna.
Las mediciones modernas del �ngulo a han demostrado que �ste es igual a 89.9°. La diferencia de 2.75° que hay entre este valor y el determinado por Aristarco es suficiente para hacer que su c�lculo fuera 20 veces menor que el resultado verdadero, que es igual a 400 veces la distancia que nos separa de la Luna.
AP�NDICE B. C�LCULO DEL VALOR DEL RADIO TERRESTRE EFECTUADO POR ERAT�STENES
La figura 9 muestra que el �ngulo formado por los rayos solares y el obelisco localizado en Alejandr�a es exactamente igual al determinado por el centro de la Tierra y el arco de c�rculo SA que separa a las poblaciones de Siena y Alejandr�a.
Erat�stenes midi� ese �ngulo y encontr� que era igual a 7° 12’, valor que es la cincuentava parte de la circunferencia terrestre, ya que
|
360�
|
|
|
|
|
=
|
50.
|
|
7�12'
|
|
|
La distancia entre Siena y Alejandr�a tambi�n fue determinada por Erat�stenes, quien despu�s de medirla contando los pasos que las separaban, encontr� que SA = 5 000 estadios. As� que multiplic� este valor por 50 para determinar la longitud de la circunferencia terrestre CT, encontrando que
Como la relaci�n que guarda la circunferencia de un c�rculo con su radio est� dada por la expresi�n
donde p es igual a 3.1416 y r es el radio de la circunferencia en cuesti�n, al sustituir los valores de la circunferencia terrestre en esta expresi�n y despejando de ella el radio se encuentra que
|
|
250 000 estadios
|
|
RT =
|
|
|
|
2p
|
de donde finalmente se obtiene que:
Como el valor del estadio se estima en 157 metros, el c�lculo de Erat�stenes en unidades modernas dar�a:
que es muy pr�ximo al que en la actualidad ha sido determinado mediante un gran despliegue t�cnico, dando como resultado que RT = 6 400 kil�metros.
Por la importancia que la elipse adquiri� despu�s de los estudios planetarios de Kepler, consideramos de inter�s hacer aqu� algunas consideraciones sobre ella.
![[FNT 88]](../img/155_270.jpg)
Figura 84. La curva cerrada conocida como elipse. Se muestran algunas de sus caracter�sticas de importancia.
La figura 84 muestra las caracter�sticas geom�tricas m�s notables de esta curva que pertenece a la familia de las secciones c�nicas, llamadas as� porque se forman cuando un cono es cortado por un plano con inclinaciones diferentes. As�, por ejemplo, cuando el plano que corta es paralelo a la base del cono, la figura que se produce es un c�rculo. Las otras curvas que resultan por los diferentes cortes son la elipse, la par�bola y la hip�rbola.
Matem�ticamente la elipse se define como la curva plana cerrada, formada por la sucesi�n de puntos tales que la suma de las distancias de cualesquiera de ellos a otros dos puntos interiores fijos llamados focos, es constante.
En la figura 84, los puntos A, B, C y D
son los v�rtices de la elipse, mientras que O es su centro. El
segmento 
es el eje mayor, el 
el eje menor, y F1 y F2
son sus focos. Las distancias r1
y r2 que unen respectivamente al punto
p con ellos son los llamados radio vectores.
Entre mayor sea la distancia del segmento 
,
mayor ser� la elipticidad de la curva, resultando m�s alargada en la direcci�n
. Al disminuir
la separaci�n entre los focos la elipse perder� ese alargamiento, hasta que
en el caso extremo, cuando F1 coincide
con F2, se tendr� que la elipse se convierte
en un c�rculo cuyo radio r = F1
= F2. Cabe aqu� comentar que en el caso
de la mayor�a de los planetas sus trayectorias el�pticas son muy pr�ximas a
c�rculos.
La ecuaci�n general que describe a la elipse est� muy bien establecida, por lo que conociendo adecuadamente los diferentes par�metros que tipifican a esta c�nica es posible determinar todas sus caracter�sticas. De ah� la gran importancia que tiene la primera ley de Kepler, pues al establecer que los planetas se mueven siguiendo trayectorias el�pticas permiti� que el tratamiento matem�tico de los datos observacionales sirviera para construir efem�rides que en todo momento permiten saber sus posiciones en la b�veda celeste.
AP�NDICE D. C�LCULO DE LAS DISTANCIAS DE J�PITER Y SATURNO AL SOL
El tiempo que un planeta emplea para regresar a un mismo punto de su �rbita se llama periodo. Si lo denotamos con la letra P, y si designamos la distancia media de un planeta al Sol con la letra a, entonces la tercera ley de Kepler puede expresarse mediante la ecuaci�n:
donde P y P' son los tiempos de revoluci�n de dos planetas en torno al Sol, y a y a' sus distancias medias a �ste.
Para el caso de la Tierra sabemos que el periodo es igual a un a�o. Si se considera que la distancia que nos separa del Sol es la unidad de medida de todo el Sistema Solar, entonces esa distancia ser� por definici�n igual a uno.
Para el caso en que se considere a la Tierra y a J�piter, la tercera ley toma la forma:
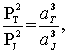
donde PT es el periodo de J�piter y
aj su distancia al Sol, que es el valor que se quiere determinar. Como
ya se dijo, PT = 1 a�o y 
T
= 1. Por otra parte, las observaciones muestran que el tiempo de revoluci�n
de J�piter en torno al Sol es de 11.86 a�os, as� que tendremos que PJ
= 11.86. Con estos valores ya se puede hallar el valor de la distancia entre
J�piter y el Sol, pues de la tercera ley se tiene que:
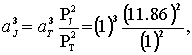
de donde 
=
140.7, lo que finalmente nos permite determinar que J=
5.2 veces la distancia entre el Sol y la Tierra, esto es
J=
5.2 UA.
Para el caso de Saturno se tiene que su periodo determinado observacionalmente es igual a 29.46 a�os, as� que haciendo las mismas consideraciones que en el caso de J�piter se tendr� que a3s = 867.9, de donde finalmente se obtiene que:
S=
9.5 UA.
Como ya se ha mencionado anteriormente (v�ase la secci�n dedicada a Cop�rnico), mientras no se determin� el valor de la unidad astron�mica no fue posible conocer las distancias planetarias en t�rminos absolutos.
AP�NDICE E. C�LCULO NEWTONIANO SOBRE LA CA�DA LUNAR
La aceleraci�n a con la que la Luna cae hacia la Tierra puede calcularse a partir del periodo de revoluci�n lunar PL y del valor del radio de la �rbita lunar ROL (figura 34). De las observaciones Newton conoc�a que PL = 27.3 d�as y que ROL = 384 550 km.
Por otra parte, el estudio del movimiento circular demostr� a Newton que el periodo de revoluci�n de un cuerpo cualquiera est� dado por la expresi�n:
|
|
2pr
|
|
P =
|
|
|
|
v
|
donde r es el radio de giro y v la velocidad con la que �ste se realiza. Adem�s, en ese tipo de movimiento la aceleraci�n centr�peta que sufre el cuerpo que se mueve circularmente est� determinada por la ecuaci�n:
|
|
v2
|
|
c= |
|
|
|
r
|
Con esta informaci�n es posible determinar la aceleraci�n que la Luna sufre en su �rbita, ya que como v = 2pr/P, se tiene que:
|
|
4p2r
|
|
c= |
|
|
|
p2
|
El radio de la �rbita lunar es igual a 384 000 000 m, mientras que el periodo de revoluci�n lunar es de 2 360 000 s. Con estos datos se encuentra que la aceleraci�n centr�peta que experimenta la Luna en su �rbita es
c
= 0.00273 m/s2.
La aceleraci�n con la que un cuerpo cualquiera cae al piso de la superficie terrestre se obtiene midi�ndola directamente:
st
= 9.8 m/s2.
De estos dos �ltimos valores se ve que la aceleraci�n centr�peta que la Luna
experimenta al moverse en su �rbita es 3 600 veces menor que la que sufren los
cuerpos al caer en la superficie terrestre. Otra forma de expresar este resultado
es diciendo que el cociente de la aceleraci�n centr�peta lunar acL
a la aceleraci�n sobre la superficie terrestre ast, es igual al inverso
de 3 600, ya que:
|
c
L |
|
0.00273
|
1
|
|
|
|
=
|
|
=0.000278=
|
|
|
S
T |
|
9.81
|
3 600
|
Por otra parte, si se toma el valor del radio terrestre que es de 6 400 km y se eleva al cuadrado, y el resultado se divide entre el cuadrado del radio de la �rbita lunar, se tendr� que:
 |
|
(6 400)2
|
1
|
|
|
|
=
|
|
= 0.000278 =
|
|
 |
|
(384 550)2
|
3 600
|
Claramente este resultado es igual al que se obtiene cuando se hace el cociente de las aceleraciones, lo que permite relacionar el movimiento de ca�da lunar hacia la Tierra con el que sufren los cuerpos al caer a la superficie terrestre. Fue as� como Newton estableci� que la fuerza que act�a en ambos casos es la misma.
AP�NDICE F. C�LCULO DE LA MASA Y DE LA DENSIDAD DE LA TIERRA
Los experimentos han demostrado que cualquier cuerpo que cae libremente en las cercan�as de la superficie terrestre sufre una aceleraci�n hacia el centro de la Tierra igual a 9.82 m/s2. De acuerdo con las leyes del movimiento desarrolladas por Newton, esa aceleraci�n implica la existencia de una fuerza constante, que proviene de la interacci�n del cuerpo en ca�da libre con todo nuestro planeta.
La fuerza que act�a sobre el cuerpo se llama peso, y puede ser calculada multiplicando la masa de �ste por la aceleraci�n con la que est� cayendo. Si w denota el peso, m la masa y g la aceleraci�n del cuerpo, entonces se tiene que:
Por otra parte, la fuerza de atracci�n gravitacional F que act�a entre el cuerpo de masa m y la Tierra puede ser calculada mediante la ley de gravitaci�n universal, que en su forma matem�tica se expresa como:
|
|
GmM
|
|
F =
|
|
|
r2
|
donde G es un valor num�rico llamado constante de gravitaci�n universal que fue determinado experimentalmente por Henry Cavendish, quien encontr� que G = 6.673 x 10-11 N m2/kg2. La masa de la Tierra es M, que es la cantidad que se va a determinar, y r es la distancia que separa a las dos masas.
Igualando el peso del cuerpo m con la fuerza de atracci�n gravitacional que �l sufre por la presencia de la masa terrestre se tiene que:
|
|
GmM
|
|
mg =
|
|
|
|
donde RT es el radio de la Tierra, ya que esa distancia es la que separa a ambos cuerpos, pues Newton demostr� que es correcto considerar que toda la masa terrestre est� concentrada en su centro. De esta �ltima ecuaci�n se tiene que:
|
|
g
|
|
M =
|
|
|
G
|
Como la aceleraci�n de la gravedad g que sufre el cuerpo m es igual a 9.81 m/s², y como se ha determinado que el radio terrestre RT mide 6 400 km, sustituyendo esos valores en la ecuaci�n anterior y realizando las operaciones correspondientes se tiene que:
valor que escrito en nuestra notaci�n cotidiana se expresa como
M = 6 021 000 000 000 000 000 000 toneladas,
que es lo mismo que 6 021 trillones de toneladas.
Evidentemente �sta es una masa gigantesca para la escala humana. Lo que es importante se�alar con este ejercicio no es lo grande que resulta la masa terrestre, pues todos tenemos conciencia de ello, lo que debe resaltarse es que es posible medirla aplicando solamente las leyes de la f�sica.
La densidad r de cualquier cuerpo se define como el cociente entre su masa M y su volumen V. En lenguaje algebraico la densidad se expresa por la relaci�n
|
|
M
|
|
r
=
|
|
|
|
V
|
Si se considera que la Tierra es una esfera de radio RT, entonces se tendr� que el volumen terrestre se puede calcular mediante la expresi�n
|
|
4
|
|
|
VT =
|
|
p
 |
|
|
3
|
|
Volviendo a tomar el radio terrestre de 6 400 km se obtiene que el volumen de nuestro planeta es igual a:
Por otra parte, ya hemos calculado la masa terrestre, y al expresarla en gramos se tiene que
Con estos dos datos ya es posible calcular el valor de la densidad terrestre, encontrando que:
Este valor significa que, si se toma un cent�metro c�bico de material terrestre, en promedio pesar� 5.48 gramos.
