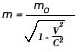|
En una etapa muy primitiva de su desarrollo, la
mente humana se formó nociones definidas del espacio y del tiempo
como el marco dentro del que tienen lugar los distintos acontecimientos.
Estas nociones, sin sufrir cambios esenciales, se han transmitido de
generación en generación y, desde la aparición
de las ciencias exactas, han constituido los fundamentos mismos de la
descripción matemática del universo. Posiblemente fue
Newton el primero en formular claramente las nociones clásicas
de espacio y tiempo, al escribir en sus Principia:
"El espacio absoluto, por su propia naturaleza y sin relación
con nada externo, persiste por siempre, inmutable e inmóvil"
y también: "El verdadero tiempo, absoluto y matemático,
por sí mismo y por su propia naturaleza, fluye uniformemente
sin relación con nada externo".
Tan arraigada estaba la convicción de que estas ideas clásicas
sobre el espacio y el tiempo eran absolutamente correctas, que los filósofos
han sostenido a menudo su carácter a priori, y ni un solo
científico llegó siquiera a imaginar la posibilidad de
dudar de ellas.
Con todo, precisamente al iniciarse el presente siglo, resultó
innegable que diversos resultados, alcanzados por los métodos
más refinados de la física experimental, conducían
a contradicciones inevitables al ser interpretados dentro del clásico
marco espacio-temporal. Fue esto lo que llevó a uno de los máximos
físicos contemporáneos, Alberto Einstein, a concebir la
idea revolucionaria de que es difícil descubrir razones, como
no sea la tradición, que obliguen a considerar absolutamente
ciertas las nociones clásicas de espacio y tiempo, que podían
y debían ser modificadas hasta que hallaran cabida en ellas los
resultados de nuestros nuevos experimentos. Es claro que, como los conceptos
tradicionales fueron formulados de acuerdo con la experiencia humana
en la vida ordinaria, no es sorprendente que los métodos refinados
de observación de que disponemos hoy en día, fundados
en una técnica experimental altamente desarrollada, indiquen
que las antiguas nociones son demasiado groseras e inexactas y que,
si pudieron aplicarse en la vida cotidiana y durante las primeras etapas
de la física, fue únicamente porque sus desviaciones respecto
de los principios correctos eran suficientemente pequeñas. Ni
tiene nada de particular que la ampliación de los campos explorados
por la ciencia moderna alcance regiones en las cuales tales desviaciones
crecen hasta el punto de volver enteramente inútiles las nociones
clásicas.
El resultado experimental más importante que condujo a la crítica
fundamental de nuestros conceptos tradicionales fue el descubrimiento
de que la velocidad de la luz en el vacío representa el límite
máximo de todas las velocidades físicamente alcanzables.
Esta conclusión tan importante y radical se deriva, ante todo,
de los experimentos del físico norteamericano Michelson, quien,
a fines del siglo pasado, intentó observar el efecto del movimiento
de la Tierra sobre la velocidad de propagación de la luz y descubrió,
para gran sorpresa suya y de todo el mundo científico, que no
existe tal efecto y que la velocidad de la luz en el vacío es
siempre la misma, independientemente del sistema desde el cual se le
mida o del movimiento de la fuente en que sea generada. No hace falta
insistir en que semejante resultado es de lo más extraordinario
y contradice nuestros más fundamentales conceptos sobre el movimiento.
Ciertamente, si un cuerpo se mueve velozmente a través del espacio
y alguien corre a su encuentro, el objeto chocará con él
con mayor velocidad relativa, igual a la suma de su velocidad y la del
observador. Si éste corre, por el contrario, en la misma dirección
y sentido que el objeto móvil, recibirá el choque por
la espalda, aunque la velocidad será menor e igual a la diferencia
de las velocidades.
De análoga manera, si se sale en un coche al encuentro de una
onda sonora que viene por el aíre, la velocidad del sonido medida
en el coche será mayor que la ordinaria, pues se le habrá
sumado la velocidad del coche, la que, en cambio, se le restaría
si el coche recibiera el sonido por detrás. Se trata del teorema
de la adición de velocidades, que siempre se consideró
evidente por sí mismo.
Sin embargo, las experiencias más cuidadosas han demostrado que,
en el caso de la luz, dicho teorema no es válido, pues la velocidad
de la luz en el vacío no altera su valor de 300 000 kilómetros
por segundo (designado siempre con la letra c), independientemente
de la velocidad del observador.
—De acuerdo —dirán ustedes—. Pero ¿no es
posible construir una velocidad mayor que la de la luz sumando velocidades
menores que la de ésta, físicamente alcanzables?
Podemos considerar, por ejemplo, el caso de un tren velocísimo,
cuya velocidad es igual a tres cuartas partes de la de la luz, y un
polizón que corre sobre los techos de los vagones, igualmente
con una velocidad de 225 000 kilómetros por segundo.
Según el teorema de la adición, la velocidad total del
polizón será una vez y media la de la luz, con lo cual
podría rebasar al rayo luminoso de un faro. En realidad, sin
embargo, como la constancia de la velocidad de la luz es un hecho establecido
experimentalmente, la velocidad resultante en este caso hipotético
debe ser inferior a la esperada, pues no puede sobrepasar el valor crítico
c. Llegamos así a la conclusión de que el teorema
de adición debe ser falso, incluso para velocidades menores.
El tratamiento matemático del problema, que no es mi intención
desarrollar aquí, conduce a una nueva fórmula sencilla,
que permite calcular la velocidad resultante de dos movimientos sobrepuestos.
Sean v1 y v2 las velocidades
que van a sumarse. La velocidad resultante es dada por
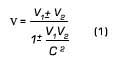
Mediante esta fórmula apreciarán ustedes que, en caso
de que ambas velocidades originales sean pequeñas —en
comparación con la de la luz, se entiende—, el término
de la derecha en el denominador de (1) podrá despreciarse si
se compara con la unidad, y así tenemos la fórmula clásica
del teorema de adición de velocidades. Pero si v1
y v2 no son pequeñas, el resultado
será siempre algo menor que la simple suma aritmética.
En el caso del polizón que corre sobre el tren,
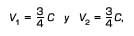
y nuestra fórmula da la velocidad resultante,
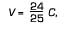
que es todavía menor que la de la luz.
En el caso particular de que una de las velocidades originales sea
igual a c, la fórmula (1) da el valor c a la
velocidad resultante, independientemente de cuál sea la segunda
velocidad. Así, sumando cualquier número de velocidades
no se puede rebasar la de la luz.
Tal vez les interese a ustedes saber que esta fórmula se ha
verificado experimentalmente y se ha encontrado que la resultante
de dos velocidades es siempre algo menor que su suma aritmética.
Una vez reconocida la existencia de la máxima velocidad posible,
podemos emprender la crítica de las ideas clásicas de
espacio y tiempo, asestando el primer golpe al concepto de simultaneidad
que de ellas se desprende.
Cuando decimos que "la explosión en las minas próximas
a la Ciudad del Cabo ocurrió exactamente en el mismo momento
en que los huevos con jamón eran servidos en nuestro departamento
de Londres", creemos saber lo que decimos. Voy a demostrarles,
sin embargo, que no es así y que, estrictamente hablando, este
enunciado carece de significado preciso. ¿Qué método,
pues, se usará para comprobar si dos acontecimientos en dos
lugares diferentes son simultáneos o no? Dirían ustedes
que el reloj marcaba la misma hora en los dos sitios, pero entonces
surge la cuestión de cómo podrían acoplarse los
relojes separados, de modo que marcasen la misma hora simultáneamente,
con lo cual caemos en el mismo problema.
En vista de que la independencia de la velocidad de la luz en el vacío
respecto del movimiento de su fuente o del sistema en que se le determine
es uno de los hechos experimentales establecidos con mayor exactitud,
hay que aceptar que el método siguiente es el más racional
para medir las distancias y acoplar los relojes correctamente. Si
reflexionan ustedes cuidadosamente, tendrán que reconocer que
es el único razonable.
Desde la estación A se envía una señal
luminosa que, al llegar a la estación B, es devuelta
instantáneamente a A. La distancia entre A y
B quedará definida como la mitad del tiempo transcurrido
en la estación A entre el envío y el regreso
de la señal, multiplicado por la velocidad de la luz, que es
constante.
Se dice que los relojes de las estaciones A y B estarán
de acuerdo si, en el momento en que llega la señal a B,
el reloj situado en ella marca la misma hora que el promedio de los
tiempos registrados en A, al partir y al retomar la señal.
Mediante este método se obtiene el marco de referencia indispensable
entre cualquier número de puestos de observación establecidos
sobre un cuerpo rígido, lo cual nos pone en condiciones de
responder a los problemas planteados por la simultaneidad de dos acontecimientos
en dos lugares diferentes, o por los intervalos de tiempo existentes
entre tales sucesos.
Ahora bien. ¿Serán aceptados los resultados así
obtenidos por parte de los observadores colocados en otros sistemas?
Para responder a esta pregunta, imaginemos que sobre dos cuerpos rígidos
diferentes se han establecido los correspondientes marcos de referencia.
Tomemos, para precisar ideas, dos largas plataformas de ferrocarril
que se mueven en direcciones opuestas, y veamos hasta qué punto
concuerdan los dos sistemas. Supongamos que en cada plataforma hay
un par de observadores, uno en cada punta, y que desean poner de acuerdo
sus relojes. Cada pareja puede aplicar en su plataforma una modificación
del método descrito, sin más que poner sus relojes en
el punto cero en el instante mismo de recibir una señal luminosa
proveniente del centro de la plataforma (medida con una vara de medir).
Así, cada pareja de observadores logrará establecer,
de acuerdo con la anterior definición, el criterio de simultaneidad
en su sistema, pues sus relojes marchan "acordes" (desde
su punto de vista, por supuesto).
Deciden ahora averiguar si los relojes de su plataforma están
de acuerdo con los de los observadores de la otra, que han hecho otro
tanto. ¿Señalarán la misma hora, por ejemplo,
los relojes de dos observadores, cada uno en una plataforma, cuando
pasen uno al lado del otro? Es fácil imaginar el experimento
siguiente: en el centro geométrico de cada plataforma instalan
un conductor eléctrico cargado, en forma tal que, cuando pasen
precisamente una junto a la otra, salte un chispazo entre los conductores
que haga partir sendas señales luminosas desde el centro de
cada plataforma, rumbo a los observadores en los extremos. Mientras
las señales luminosas, que avanzan a velocidad finita, se acercan
a los observadores, la posición relativa de las plataformas
cambia en tal forma que los observadores N1 (en
la plataforma A) y N4 (en la plataforma
B) se aproximan al punto del que partió la luz, en tanto
que a los observadores N2 y N3
les sucede lo contrario.
Es claro que cuando la señal luminosa alcance al observador
N1 (plataforma A,) el observador N3
habrá retrocedido un poco, haciendo que la señal tarde
algo más en llegar a él. Así que, en caso de
que el reloj de N3 marche en tal forma que
marque el tiempo cero a la llegada de la señal, el observador
N1 insistirá en que el reloj de N3
va atrasado.
De la misma manera, otro observador, N2,
sobre la plataforma A, llegará a la conclusión
de que el reloj de N4 (plataforma B),
quien recibió la señal antes que N2,
anda adelantado. Hemos aceptado que la pareja de observadores de la
plataforma A está de acuerdo en su definición
de la simultaneidad y que sus relojes marchan acordes: sus observaciones
harán aceptar a ambos, sin embargo, que los relojes de los
observadores en la plataforma B no están de acuerdo
entre sí. Mas no hay que olvidar que otro tanto ocurre con
los observadores de la plataforma B; quienes aceptarán
que sus propios relojes tienen la misma marcha, pero llegarán
a la conclusión de que no ocurre otro tanto con los relojes
de la plataforma A.
Dado que ambas plataformas son perfectamente equivalentes, esta discusión
entre los dos grupos de observadores sólo podrá zanjarse
diciendo que cada pareja tiene razón desde su propio punto
de vista, pero que el problema de saber quiénes están
"absolutamente" en lo cierto no tiene sentido físico.
Temo haberlos cansado demasiado con estas largas consideraciones,
pero confío en que, si las siguen ustedes cuidadosamente, acabarán
por aceptar que, adoptando nuestro método para las medidas
espacio-temporales, el concepto de simultaneidad absoluta se desvanece
y que un par de acontecimientos en lugares diferentes, considerado
simultáneo desde un sistema de referencia, se veía separado,
desde un segundo sistema, por un intervalo definido de tiempo.
Esta proposición suena muy rara al principio, pero aparece
como bien natural si decimos que, comiendo en el tren, ingerimos de
la sopa al postre en el mismo punto del vagón comedor, pero
en puntos muy separados sobre la vía del ferrocarril. Este
enunciado, sin embargo, equivale a decir que dos acontecimientos
diferentes en un solo punto de un sistema de referencia se verán
separados por un espacio definido, desde el punto de vista de un segundo
sistema.
Al comparar esta proposición tan "trivial" con la
otra, tan "paradójica", apreciarán ustedes
que son enteramente simétricas, e interconvertibles con sólo
intercambiar las palabras "tiempo" y "espacio".
Y éste es el punto clave de la teoría de Einstein: mientras
la física clásica aceptaba el tiempo como algo absolutamente
independiente del espacio y el movimiento, "fluyendo uniformemente
sin relación con nada externo" (Newton), para la física
nueva el espacio y el tiempo están íntimamente ligados
y representan, ni más ni menos, dos secciones a lo largo de
un "continuo espacio-temporal" homogéneo en el cual
se producen todos los acontecimientos observables. La resolución
de este continuo de cuatro dimensiones en espacio tridimensional y
tiempo unidimensional es puramente arbitraria, y depende del sistema
desde el cual se efectúen las mediciones.
Dos acontecimientos separados, para un sistema dado, por la distancia:
l en el espacio y el intervalo t en el tiempo, resultarán
separados por una distancia diferente, 1', y un intervalo de
tiempo distinto, t ,,al ser considerados desde otro
sistema, lo cual en cierto modo nos autoriza a hablar de transformación
de espacio en tiempo y viceversa. Tampoco es difícil comprender
por qué estamos enteramente acostumbrados a la transformación
de tiempo en espacio —recuérdese la comida en el tren—,
en tanto que el caso inverso, que conduce a la relatividad de la simultaneidad,
se nos antoja bien poco común. Es que si medimos las distancias
en "centímetros", por ejemplo, la correspondiente
unidad de tiempo no debería ser el "segundo" ordinario,
sino cierta "unidad racional", representada por el intervalo
de tiempo que necesita cualquier señal luminosa para recorrer
la distancia de un centímetro, o sean 0.00000000003 segundos.
Es claro que, en el campo de la experiencia ordinaria, la transformación
de intervalos de espacio en intervalos temporales conduce a resultados
prácticamente inobservables; de aquí que parezca correcto
el concepto clásico según el cual el tiempo es algo
enteramente independiente e inmutable.
Sin embargo, si investigamos movimientos con velocidades enormes,
como en los electrones emitidos por los cuerpos radiactivos, o en
los que corren dentro de los átomos, casos, en fin, en que
las distancias cubiertas en determinado intervalo de tiempo son del
mismo orden de magnitud que ese intervalo expresado en unidades racionales,
en esos casos, digo, tropezamos sin remedio con los dos efectos que
hemos discutido, y la teoría de la relatividad adquiere importancia
capital. Bastan velocidades un tanto reducidas, como las de los planetas
en nuestro sistema solar, para hacer observables los efectos relativistas,
gracias, desde luego, a la extremada precisión de las medidas
astronómicas. Señalemos sólo que la observación
de tales efectos exige apreciar cambios en los movimientos planetarios
que ascienden apenas a una fracción de segundo angular por
año.
He intentado explicar a ustedes cómo la crítica de las
nociones de espacio y tiempo lleva a la conclusión de que los
intervalos espaciales son parcialmente convertibles en intervalos
temporales y viceversa, lo cual implica que el valor numérico
de una distancia o periodo determinados variará con el sistema
en movimiento desde el cual se verifique la medición.
Un aná1isis matemático relativamente sencillo de este
problema, que no es mi intención exponer ahora, conduce a una
fórmula definida que expresa el cambio sufrido por ambas magnitudes.
Todo objeto de longitud 1, en movimiento relativo respecto
al observador con velocidad v, se acortará en función
de esta velocidad, haciendo que su longitud sea igual a
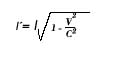 (2) (2)
De análoga manera, cualquier proceso que se lleve un tiempo
t será observado desde el sistema en movimiento relativo
como si se llevara un tiempo mayor, t´ dado por
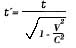 (3)
(3)
Esto es el famoso "acortamiento del espacio" y la "dilatación
del tiempo" de la teoría de la relatividad.
Lo común es que v sea muy inferior a c, lo cual
reduce los efectos relativistas hasta la insignificancia; pero, al
alcanzar velocidades suficientes, las longitudes medidas desde un
sistema en movimiento llegan a reducirse y los intervalos de tiempo
a alargarse tanto como se desee.
Debo insistir en que ambos efectos constituyen sistemas absolutamente
simétricos, así que mientras los pasajeros de un tren
que se mueve velozmente se asombrarán de la delgadez y lentitud
de movimientos de los que ocupan un tren detenido, otro tanto pensarán
estos últimos de los viajeros del tren en movimiento.
Otra consecuencia importante de la existencia de una velocidad máxima
afecta a las masas de los cuerpos en movimiento. De acuerdo con los
fundamentos mismos de la mecánica, la masa de un cuerpo determina
la dificultad con que se tropieza para ponerlo en movimiento o para
acelerar un movimiento ya existente; cuanto mayor es su masa tanto
más difícil es incrementar su velocidad en un valor
determinado.
El hecho de que, en ninguna circunstancia, ningún cuerpo puede
exceder en velocidad a la luz, nos conduce directamente a la conclusión
de que su resistencia a la aceleración o, en otras palabras,
su masa, debe incrementarse ilimitadamente conforme su velocidad se
aproxima a la de la luz. El análisis matemático conduce
a la fórmula de esta dependencia, que es análoga a las
fórmulas (2) y (3). Sí m0 es
la masa a velocidades muy pequeñas, la masa m a velocidad
v será
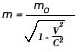
y la resistencia a la aceleración tiende al infinito cuando
v se acerca a c.
Es fácil observar experimentalmente esta modificación
relativista de la masa en las partículas muy veloces. Por ejemplo,
la masa de los electrones emitidos por las sustancias radiactivas
(a velocidad igual al 99% de la velocidad de la luz) es varias veces
mayor que la observada en las partículas en reposo. Y las masas
de los electrones que constituyen los rayos llamados cósmicos,
tan rápidos que alcanzan sin dificultad el 99.98% de la velocidad
de la luz, son 1 000 veces mayores que la masa del electrón
en reposo. Por lo que toca a tales velocidades, la mecánica
clásica resulta del todo inútil y entramos en los dominios
de la pura teoría de la relatividad.
|
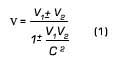
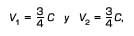
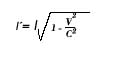 (2)
(2)
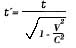 (3)
(3)