6. Determinaci�n del volumen de la materia

Corresponde a la sesi�n de GA 7.6 DIMENSIONES Y M�S DIMENSIONES

Como se dijo anteriormente, toda la materia ocupa un lugar en el espacio, es decir, tiene volumen.

El volumen es una magnitud que, generalmente, se expresa en las siguientes unidades: metro c�bico (m�), dec�metro c�bico (dm�), cent�metro c�bico (cm�) mil�metro c�bico (mm�); cabe aclarar que 1 cm� = 1 ml.

Para obtener el volumen de un cuerpo hay que tomar en cuenta su forma y el estado f�sico que presenta. A continuaci�n se explica la medici�n del volumen de s�lidos con forma regular, de l�quidos y de gases y, por �ltimo, de cuerpos s�lidos de forma irregular.

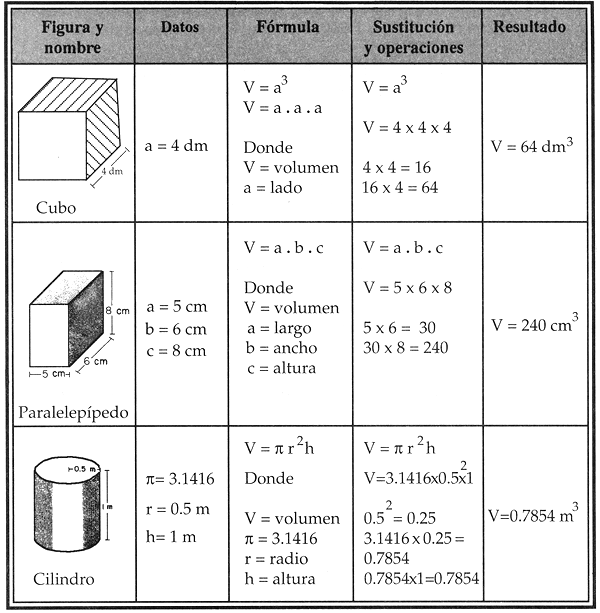
El volumen de s�lidos de forma regular -como el cubo, el paralelep�pedo y el cilindro-, se obtiene utilizando una f�rmula espec�fica, que en general multiplica el �rea de la base por la altura. Ejemplos:

Otros cuerpos de forma regular y sus f�rmulas correspondientes para determinar el volumen son:

Los l�quidos adoptan la forma del cuerpo que los contiene, por lo tanto, el volumen de los l�quidos se puede obtener utilizando cuerpos de forma regular, como recipientes cil�ndricos o en forma de paralelep�pedo, que sean de material r�gido.

Por ejemplo, en el caso de utilizarse un recipiente cil�ndrico, como una lata de refresco, se deben tomar sus medidas, las cuales corresponden al di�metro interno para conocer el radio y la altura a la que llega el l�quido.

Si el cilindro es transparente, se determina la altura midiendo hasta el menisco, el cual es la parte m�s baja de la curvatura que se forma en la superficie del l�quido.

Si se trata de un cuerpo opaco, la altura se puede determinar midiendo la distancia del nivel del l�quido al borde, la que se resta de la altura total del recipiente.

Con los datos obtenidos, se utiliza la formula correspondiente.

Para medir el volumen de un gas, se puede recurrir tambi�n al uso de cuerpos de forma regular, porque la materia en este estado no tiene volumen ni forma propios. Uno de los procedimientos que se puede seguir es el que se explica a continuaci�n:

En un recipiente con agua se introduce, en forma vertical, un vaso invertido, sumergi�ndolo hasta el fondo. El vaso, en su interior, aloja aire; esta mezcla, como toda la materia, tiene la propiedad de la impenetrabilidad, por lo cual el agua no puede penetrar en �l. Si el vaso est� graduado, solamente se identifica el volumen que ocup� el aire, delimitado por el nivel del l�quido. Si el recipiente no est� graduado, se determina el volumen ocupado con el procedimiento descrito en los l�quidos.

Para obtener el volumen de cuerpos s�lidos irregulares, es decir, sin una forma definida (por ejemplo una piedra), se sumergen en un recipiente graduado con agua. En este caso, el nivel del agua sube de acuerdo con el volumen de la piedra, porque seg�n la propiedad de impenetrabilidad, dos cuerpos no ocupan un mismo espacio en el mismo tiempo.

Con este procedimiento, del volumen total del cuerpo y el agua se resta el que ocupa el l�quido solo. As�, por ejemplo, si el nivel del agua con la piedra midi� 158 cm�, y sin ella es de 120 cm� , la diferencia de 38 cm� corresponde al volumen de la piedra.

El volumen de un cuerpo s�lido irregular se puede obtener de esta forma, siempre y cuando el s�lido no sea poroso ni soluble en el l�quido.