8. Adici�n y sustracci�n de polinomios

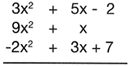
Corresponde a la sesi�n de GA 2.8 UNA REDUCCI�N NECESARIA

En �lgebra tambi�n se llevan a cabo operaciones como las que se realizan en aritm�tica.

De hecho, las operaciones de adici�n y sustracci�n de polinomios se realizan entre t�rminos que son de la misma especie, lo cual significa que no es posible sumar o restar t�rminos que no son semejantes. Por ejemplo: si se tiene una calculadora que se representa con (c) y una escuadra representada con (e) no es posible obtener la suma, ya que no son t�rminos semejantes.

Los t�rminos semejantes son aquellos que tienen las mismas literales con los mismos exponentes, aunque los coeficientes sean distintos.

Ejemplos:

7a�b�

-9a�b�

a�b�

Los t�rminos no semejantes son aquellos que, aunque presentan el mismo coeficiente, la letra y el exponente es diferente.

9ab�

9a�

9ab

Una vez identificados los t�rminos semejantes es conveniente proceder a reducirlos conforme a lo siguiente:

Cuando se tienen t�rminos semejantes, en los cuales los coeficientes tienen igual signo, �stos se suman y el resultado conservar� el signo; la parte literal ser� la misma:

7x + 9x = 16x

-5y -3y = -8y

Otra situaci�n a considerar para reducir t�rminos semejantes es cuando los coeficientes tienen signos diferentes. Aqu� se procede a restar los valores absolutos y al resultado se le coloca el signo del sumando de mayor valor absoluto seguido de la parte literal:

-4a� + 2a� = -2a�

15a� -5a� = 10a�

Para realizar una adici�n de polinomios hay que tomar en cuenta las siguientes recomendaciones:

a) Ordenar los polinomios en orden decreciente (de mayor a menor con respecto a la literal).

b) Los t�rminos se colocar�n en columna (forma vertical), procurando que los t�rminos semejantes coincidan en la misma columna.

Ejemplo:

Si se tiene:

(5x + 3x� -2) + (9x� + x) + (7 + 3x -2x�)

Se ordenan en forma decreciente y se colocan verticalmente los t�rminos que son semejantes

Posteriormente se reducen los t�rminos semejantes de los polinomios, quedando:

Para realizar la sustracci�n de polinomios se procede a sumar al polinomio minuendo el sim�trico del polinomio sustraendo. El sim�trico de cada t�rmino del sustraendo se obtiene al multiplicarlo por -1 (menos uno).

Ejemplo:

(9x� +3x - 5) - (5x� + 2x - 3)

Sim�trico de

5x� + 2x - 3 es -5x� - 2x +3