13. Ecuaciones con dos inc�gnitas

Corresponde a la sesi�n de GA 2.13 DESC�BRELAS

Es importante conocer este tipo de ecuaciones y dominarlas, ya que sirven para resolver una gran variedad de problemas, los cuales se pueden trazar e interpretar gr�ficamente.

Las ecuaciones de primer grado con dos inc�gnitas son conocidas como ecuaciones indeterminadas, ya que tienen una infinidad de soluciones. Tambi�n se les conoce como ecuaciones lineales, en virtud de que su gr�fica es una l�nea recta.

Los problemas que aqu� se plantean ayudar�n a comprender m�s f�cilmente las ecuaciones con dos inc�gnitas, por ejemplo:

1. Ren� realiz� 2 ex�menes y su maestro le dijo que la suma de sus dos calificaciones era 10. �Qu� calificaci�n obtuvo Ren� en cada examen?

Los datos desconocidos se indicar�n con dos literales: el primer examen se identifica con la x y el segundo examen con la y, por lo tanto se formula la siguiente ecuaci�n:

x + y = 10

Hay que buscar los valores de las literales, por lo que se procede a despejar y y asignarle valores arbitrarios a x.

Despejando y, se obtiene:

y = 10 - x

Al dar valores arbitrarios a x, se efectuar�n las operaciones y se obtendr�n los valores de y, para esto se construir� una tabla que refleje algunas soluciones.

Donde:

y = 10 - x

si x = 0 si x = 6 si x = 8 si x = 10

y = 10 - 0 y = 10 - 6 y = 10 - 8 y = 10 - 10

y = 10 y = 4 y = 2 y = 0

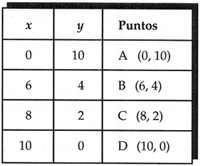
Como puede observarse, �stas son algunas de las soluciones para el problema planteado:

a) Si en el primer examen obtuvo cero, en el segundo la calificaci�n fue de diez.

b) Si en el primer examen obtuvo seis, en el segundo la calificaci�n fue de cuatro.

c) Si en el primer examen obtuvo ocho, en el segundo la calificaci�n fue de dos.

d) Si en el primer examen obtuvo diez, en el segundo la calificaci�n fue de cero.

De lo anterior, se observa que para cualquier valor asignado a x existe uno para y, por lo que no hay una soluci�n �nica para el problema.

Si se considera que cada pareja de valores corresponde a las coordenadas de algunos puntos, la tabulaci�n quedar�a as�:

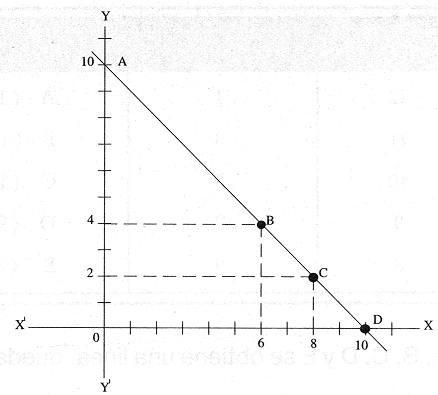
Y su representaci�n gr�fica es la siguiente:

Como puede apreciarse en la gr�fica, la soluci�n de la ecuaci�n es una l�nea recta, donde cada uno de los puntos de la l�nea resultante representa una pareja de coordenadas de x y y que hacen verdadera la ecuaci�n.

2. Esperanza va a comprar un vestido que cuesta $250, el cual va a pagar con monedas de $20 y $ 10.�Cu�ntas monedas de $20.00 y $ 10.00, necesitar� para comprar el vestido?

Al analizar el problema se sabe que se necesitan x monedas de $20.00, as� como y monedas de $ 10.00, quedando la ecuaci�n:

20x + 10y = 250

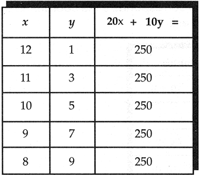
Este problema tiene muchas soluciones que pueden satisfacer las condiciones dadas. En la siguiente tabla, se dan diferentes valores a las inc�gnitas para apreciar las diversas soluciones que tiene:

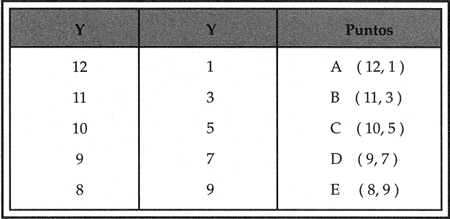
De las soluciones consideradas se obtienen algunas parejas de valores de x, y, que satisfacen lo requerido en la ecuaci�n del problema y, si se considera que esas parejas son coordenadas de puntos, se tiene la siguiente tabulaci�n:

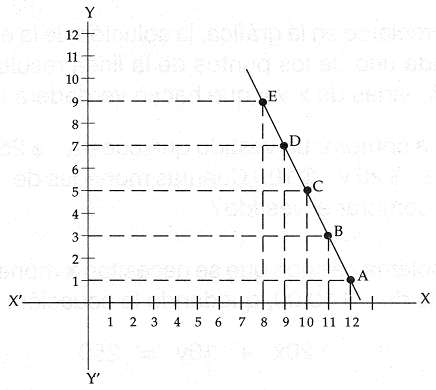
Con los puntos A, B, C, D y E se obtiene una l�nea, quedando la representaci�n gr�fica as�:

Mediante la gr�fica trazada se pueden dar diversas lecturas a las respuestas de la pregunta del problema, por ejemplo:

Se necesitan doce monedas de $20.00 y una de $10.00 para pagar los $ 250.00

o bien

Se necesitan nueve monedas de $ 20.00 y siete de $10.00 para pagar los $250.00

Por todo lo anterior se puede decir que es importante conocer, dominar y aplicar las ecuaciones con dos inc�gnitas, para resolver muchos de los problemas que pueden tener varias soluciones.