14. Sistemas de Ecuaciones

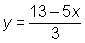
Corresponde a la sesi�n de GA 2.14 UNA EN OTRA

Existen diversas formas algebr�icas para resolver un sistema de ecuaciones simult�neas con dos inc�gnitas.

El m�todo de sustituci�n es una de esas formas y recibe ese nombre debido a las sustituciones que se realizan durante su desarrollo.

Para ejemplificar el procedimiento v�ase el siguiente problema:

Josefina compr� 5 tamales y 3 atoles y pag� $13.00; H�ctor pag� $14.00 por 4 tamales y 6 atoles. �Cu�nto costaba cada tamal y cada atole?

Analizando el problema, se parte de lo que sigue:

x = costo de tamales

y = costo de atoles

El problema queda representado algebr�icamente por medio de este sistema:

5x + 3y = 13 (1)

4x + 6y = 14 (2)

Al despejar y en la ecuaci�n (1), se tiene:

Una vez despejada y en la ecuaci�n (1), se sustituye �sta en la ecuaci�n (2).

Para resolver esta ecuaci�n se procede a eliminar el par�ntesis, multiplicando el factor por la fracci�n.

Ahora, hay que eliminar el denominador, multiplicando cada miembro de la ecuaci�n por 3.

De donde se obtiene:

12x + 78 = -30x = 42

El siguiente paso consiste en eliminar el t�rmino independiente, sumando -78 en los dos miembros.

12x + 78 - 78 -30x = 42 -78

Queda as�:

12x - 30x = -36

Muy bien, ahora hay que reducir t�rminos semejantes en ambos miembros:

-18x = -36

Finalmente hay que dividir ambos miembros entre -18, para despejar la inc�gnita.

Obteni�ndose:

x = 2

Sustituyendo a x por su valor en la ecuaci�n 1, ya despejada, se tiene:

Al realizar las operaciones se�aladas se tiene que:

y = 1

Por lo tanto, el valor de y es igual a 1.

La soluci�n del problema es �sta: el costo de un tamal (representado con x) es igual a $ 2.00, y el costo de cada atole (representado con y) es de $1.00.

Al respecto, se procede a comprobar el sistema de ecuaciones, sustituyendo las inc�gnitas por los valores obtenidos.

5x + 3y = 13 (1)

4x + 6y = 14 (2)

Comprobaci�n de la ecuaci�n (1).

5x + 3y = 13

5 (2) + 3 (1) =13

10 + 3 = 13

13 = 13

Comprobaci�n de la ecuaci�n (2).

4x + 6y = 14

4 (2) + 6 (1) =14

8 + 6 = 14

14 = 14

Como puede apreciarse, se han cumplido las igualdades en cada ecuaci�n y, por lo tanto, quedan comprobados los valores de x y de y.

La resoluci�n de sistemas de ecuaciones simult�neas tienen aplicaci�n cuando se requiere resolver problemas semejantes a estos, por lo cual es conveniente dominar diversos m�todos de soluci�n.