1. Funciones

Corresponde a la sesi�n de GA 2.1 RECTAS Y CURVAS

En econom�a, es com�n hablar de las leyes de la oferta y la demanda. La ley de la oferta se refiere a la cantidad disponible de un producto que se lleva al mercado para su consumo. La de la demanda nos habla de la cantidad que un cierto p�blico compra de ese producto. La relaci�n que se establece entre estas dos variables es una de las relaciones conocidas en matem�ticas como funciones.

Si dos variables, x y y, est�n relacionadas de tal forma que, para cada valor asignado a x, queda determinado un valor de y, se dice entonces que y est� en funci�n de x. A la variable que se le asignan valores (x) se le denomina variable independiente, pues �sta puede tomar cualquier valor; por lo tanto, a la otra se le conoce como variable dependiente, ya que el valor que �sta adquiera depender� del valor que se le asigne a la variable independiente.

Una funci�n responde a una regla en la que se establece la relaci�n existente entre las variables x y y, de tal manera que, conociendo los valores asignados a x, es posible obtener valores para y, y representar estos gr�ficamente.

Por ejemplo:

y = 2x +3

1= x� -1

En este apartado se representar�n, en forma gr�fica, las funciones lineales o de primer grado y las funciones cuadr�ticas o de segundo grado.

Una funci�n lineal o de primer grado se caracteriza porque el t�rmino x no tiene exponente 1.

Ejemplos de este tipo de funci�n son:

y = 3x - 1; y = -x + 2; y = -2x - 4; y = 4x + 1, etc�tera.

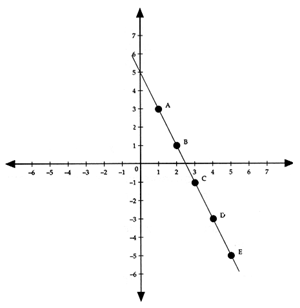
Para obtener la gr�fica de la funci�n y = -2x + 5, por ejemplo, se procede a tabular, es decir, se dan valores a la variable independiente x y se busca (por medio de las operaciones indicadas) el valor de la variable dependiente y, como se ilustra a continuaci�n.

Funci�n: y = -2x + 5

x	y	Puntos
1	3	A(1,3)		y = -2(1)+5 = -2+5 = 3
2	1	B(2,1)		y= - 2(2)+5 = -4+5 = l
3	-1	C(3,-1)		y= - 2(3)+5 = -6+5 = -l
4	-3	D(4,-3)		y = - 2(4)+5 = -8+5 = -3
5	-5	E(5,-5)		y = - 2(5)+5 = - 1O+5 = -5

Una vez que los valores se han tabulado, se procede a representarlos gr�ficamente.

La gr�fica de una funci�n de primer grado se llama tambi�n funci�n lineal porque su gr�fica es siempre una l�nea recta.

Generalizando, una funci�n lineal o de primer grado es de la forma y = mx + b, donde m y b pueden tener valores positivos o negativos

Respecto de la funci�n cuadr�tica o de segundo grado, �sta se caracteriza por tener el t�rmino x con exponente �; ejemplos de esta funci�n son:

y = X� +5; y = -3x�+1; y = 4x�-1; y = (x -3)�, etc�tera.

Para obtener la gr�fica de la funci�n y = (x - 3)�, se procede a tabular. Se dan valores a la variable independiente x y, resolviendo las operaciones indicadas, se van obteniendo los valores de la variable dependiente y. As�, se tiene que:

Funci�n y = (x - 3)�

x	y	Puntos
1	4	A(1,4)		y(1-3)� = (- 2)�=4
2	1	B(2,1)		y=(2--3)� =(- l)� =1
3	0	C(3,0)		y=(3-3)� = (0)�=0
4	1	D(4,1)		y(4-3)� =(1)� =1
5	4	E(5,4)		y=(5-3� = 2 (2)�=4

Una vez tabulados los valores, �stos se representan gr�ficamente de la siguiente manera:

La gr�fica de una funci�n de segundo grado se llama tambi�n funci�n cuadr�ticas y su gr�fica es una curva llamada par�bola.

La utilidad de las funciones lineales y cuadr�ticas encuentra un campo f�rtil. En la ciencia y la t�cnica, justificando con ello, la dimensi�n que la herramienta matem�tica ha alcanzado en estas �reas.