2. Leyes de los exponentes

Corresponde a la sesi�n de GA 2.2 A TODA LEY

A la operaci�n matem�tica que representa, en forma abreviada, la multiplicaci�n de factores iguales se le llama potenciaci�n.

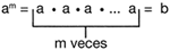
La potenciaci�n, como expresi�n algebraica, la conforman los siguientes elementos:

a = base

m = exponente

b = potencia

As� se tiene que:

Con base en esta definici�n es posible entender las leyes de los exponentes.

Primera ley: Producto de potencias con la misma base.

Ejemplo:

a� � a�

Por la definici�n de potencia se tiene:

donde a aparece 5 veces como factor, por lo tanto:

a� � a� = a�+�

=

Al generalizar se afirma que:

El producto de potencias con la misma base (distinta de cero) es igual a la base elevada a la suma de los exponentes.

Segunda ley: Cociente de potencias con la misma base

Ejemplo:

Por la definici�n de potencia se tiene:

Al cancelar factores iguales queda:

Al generalizar queda:

El cociente de potencias con la misma base es igual a la base elevada a la diferencia de los exponentes.

Obs�rvese ahora el siguiente ejemplo:

y se sabe que:

Por transitividad:

De lo que se concluye que:

Todo n�mero exponente negativo es igual a su inverso con exponente positivo

Tercera ley: Potencia de una potencia

Ejemplo:

Por la definici�n de potencia se tiene:

Apoy�ndose en la ley 1;

Generalizando se tiene que:

La potencia de otra potencia de la misma base (distinta de cero) es igual que la base elevada al producto de los exponentes.

Cuarta ley: Potencia de un producto

Ejemplo: (ab)�

Al aplicar la definici�n de potencia:

(ab)� = ab � ab � ab

Aplicando la ley conmutativa:

(ab)� = a � a � a � b � b � b

Y como la potencia es una multiplicaci�n abreviada, queda:

a�b�

Generalizando, se tiene que:

La potencia de un producto es igual que el producto de la misma potencia de los factores

Quinta ley: Cuando un cociente se eleva a una potencia

Ejemplo:

Aplicando la definici�n de potencia:

Abreviando la multiplicaci�n de fracciones:

Al generalizar se tiene que:

Para elevar una fracci�n a un exponente se eleva el numerador y el denominador a dicho exponente.

Los siguientes casos se deducen de las leyes anteriores. En la divisi�n de potencias de la misma base y exponente se aplica la segunda ley y resulta que:

Pero el cociente de la divisi�n (cuando el divisor y dividendo son iguales) es 1, entonces:

Por transitividad:

a� = 1

De donde se generaliza que:

Todo n�mero diferente de cero con exponente 0 es igual a 1

Si se tiene la expresi�n:

Aplicando la definici�n de potencia:

Se cancelan los dividendos y divisores iguales y se tiene:

Por transitividad:

a� =a

Generalizando:

Todo n�mero elevado a la primera potencia es igual que ese mismo n�mero

Menci�n especial merece el caso de la potenciaci�n con exponente fraccionario.

Ejemplo:

Si se eleva a la potencia que indica el denominador del exponente resulta que:

Por la definici�n:

Aplicando la primera ley de los exponentes, se tiene:

Por la propiedad transitiva:

Si se extrae la ra�z cuadrada a ambos miembros de la igualdad, se tiene:

Al eliminarse la ra�z y la potencia (por ser operaciones inversas), se tiene que:

Generalizando:

En la resoluci�n de expresiones algebraicas, la aplicaci�n correcta de estas leyes ser�n de fundamental importancia para la obtenci�n del resultado que se busca.