Corresponde a la sesi�n de GA 2.11 UNA RELACI�N NO AFECTIVA
Desde el punto de vista geom�trico, el estudio del c�rculo ha resultado ser muy interesante, y lo es m�s cuando se logra encontrar la relaci�n que existe entre los elementos que lo constituyen.
Hay una gran cantidad de cuerpos y objetos que presentan esta figura, como el caso de una moneda, la base de recipientes en forma cil�ndrica, la rueda de una bicicleta, etc�tera.
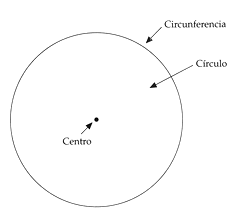
Antes de profundizar en el tema, es conveniente considerar que no hay que confundir lo que es la circunferencia con el c�rculo; por ello se procede a identificar ambas partes en la siguiente figura.
Como puede observarse en la figura anterior, el contorno es la circunferencia, en tanto que el interior es el c�rculo.
A continuaci�n se identificar�n las rectas que cortan o tocan a la circunferencia, as� como la que se encuentra ubicada fuera de la misma.
La recta (1) corta la circunferencia en dos puntos; por lo tanto, se tiene que los puntos de esta recta son tanto interiores como exteriores a la circunferencia. Este tipo de rectas son conocidas como secantes.
La recta (2) toca a la circunferencia en un solo punto, el cual recibe el nombre de punto de tangencia; los dem�s puntos de la recta se localizan en el exterior de la circunferencia. Este tipo de rectas son conocidas como tangentes.
La recta (3) se encuentra fuera de la circunferencia, es decir, se ubica en el exterior de la misma y, por no tener ning�n punto de contaco con ella, se le conoce como recta exterior.
Ahora se identificar�n, en la siguiente figura, los segmentos y arcos que se pueden trazar en el c�rculo o en la circunferencia, seg�n sea el caso.
Como puede observarse, en la figura se han trazado los siguientes segmentos de recta.
El segmento AB es un radio del c�rculo. Cada punto de la circunferencia es el extremo de otro radio. Un radio es el segmento que une al centro del c�rculo con un punto cualquiera de la circunferencia.
El segmento CD es una cuerda del c�rculo. Cada par de puntos de la circunferencia determina una cuerda del circulo una cuerda es un segmento que une dos puntos cualesquiera de la circunferencia.
El segmento GH es un di�metro del c�rculo. El di�metro del c�rculo es un segmento que une dos puntos de la circunferencia y pasa por el centro del c�rculo; se le considera como la cuerda de mayor tama�o que divide al c�rculo en dos partes congruentes
LM es un arco del c�rculo. Se define un arco como la parte continua de la circunferencia, limitada o comprendida entre dos puntos extremos, y se escribe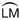 
para representarlo.
El v�rtice del �ngulo ABC es el centro del c�rculo. <ABC es un �ngulo central. Un �ngulo central es un �ngulo cuyo v�rtice est� en el centro del c�rculo.
El v�rtice del �ngulo DEF es un punto de la circunferencia; los lados del �ngulo intersecan la circunferencia en los puntos D y F. <DEF es un �ngulo inscrito. Un �ngulo inscrito es un �ngulo cuyo v�rtice es un punto de la circunferencia y cuyos lados contienen una cuerda del c�rculo.
El v�rtice del �ngulo GHI es un punto de la circunferencia y sus lados lo forman una tangente y una secante del c�rculo. <GHI es un �ngulo semiinscrito.
Como puede observarse en la figura anterior, al trazar un �ngulo central en el c�rculo, una parte de la circunferencia queda limitada por los lados del �ngulo trazado, por lo que se considera a esa porci�n como arco subtendido asociado al �ngulo que lo determin�.
La medida en grados de un arco se determina por la medida de su �ngulo central asociado; por ejemplo:
A partir de la medida en grados de un arco se puede determinar su longitud, al considerar los 360� que mide la circunferencia y conocer la medida de su di�metro para calcular su longitud. Por ejemplo: si el di�metro del c�rculo anterior mide 5 cm, la circunferencia medir�:
3.14 x 5 = 15.70. Al establecer la proporci�n tenemos
As� que, en este c�rculo, a un arco de 60� corresponde una longitud de 2.61 cm.
Al observar en la figura anterior el �ngulo central AOC y el �ngulo inscrito ABC, que determinan el mismo arco, puede afirmarse que la medida de un �ngulo inscrito es igual a la mitad del �ngulo central correspondiente.
Con la finalidad de aplicar la relaci�n que hay entre las rectas, segmentos y �ngulos anteriormente considerados, se utilizar�n las bisectrices de un tri�ngulo, como se indica a continuaci�n.
Al trazar las tres bisectrices de cada uno de los �ngulos del tri�ngulo ABC, se observa que se cortan en un mismo punto, situado en el interior del tri�ngulo; este punto se llama incentro y es el centro del c�rculo inscrito en el tri�ngulo, el cual toca los tres lados del mismo. Los lados del tri�ngulo son tangentes porque tienen un punto de contacto con la circunferencia; las bisectrices son secantes porque cortan a la circunferencia en dos de sus puntos.
Por �ltimo, se utilizar�n las mediatrices con el mismo fin: aplicar en la pr�ctica la relaci�n de rectas, segmentos y �ngulos.
Al trazar las tres mediatrices del tri�ngulo ABC, el cual se encuentra dentro de un c�rculo, se observa que se cortan en un mismo punto, llamado circuncentro; �ste es el centro del c�rculo circunscrito a la figura y cuya circunferencia toca sus tres v�rtices; por lo tanto, las mediatrices son secantes y los lados del tri�ngulo son cuerdas.
Estas secantes y cuerdas, al cortarse, forman �ngulos rectos, puesto que son perpendiculares.
El conocimiento de las relaciones que se pueden establecer entre las diversas l�neas del c�rculo enriquece e incrementa el acervo de la geometr�a.
![[ Índice Conceptos Básicos ]](toc.gif)
![[ Previo ]](prevsec.gif)
![[ Nivel Superior ]](parntsec.gif)
![[ Siguiente ]](nextsec.gif)
