10. Ecuaciones cuadr�ticas completas

Corresponde a la sesi�n de GA 2.10 ENCUENTRA LAS RA�CES

Hasta este momento se sabe c�mo resolver ecuaciones cuadr�ticas incompletas (puras y mixtas). Ahora se ver� c�mo se resuelven las cuadr�ticas completas. Para tal fin, recu�rdese que en el texto 2.9 se plante� un problema que da origen a una cuadr�tica completa y cuya soluci�n no se obtuvo. Dicho problema es el siguiente:

El grupo de danza folkl�rica de una comunidad va a participar en un concurso regional. No conoce el sal�n en el que se llevar� a cabo la competencia, pero requiere saber cu�les son sus dimensiones para armar su coreograf�a. La �nica persona del grupo que conoce el sal�n informa que existe una pista de baile cuya �rea es de 70 m� y en la cual el largo mide 3 m m�s que el ancho. Pero, �cu�nto mide de largo y cu�nto de ancho?

La soluci�n del problema se plantea traduciendo al lenguaje algebraico lo que est� expresado en lenguaje com�n, y entonces:

Si el ancho de la pista se representa con x, el largo tiene que ser x + 3

como el �rea se obtiene multiplicando largo por ancho, se origina la ecuaci�n:

(x + 3) x = 70

se realiza la multiplicaci�n indicada y resulta:

x� +3x = 70

como ya se vio, la forma general de una ecuaci�n cuadr�tica completa es:

ax� + bx + c = 0

Para que se pueda apreciar claramente esa forma en la ecuaci�n planteada, se requiere eliminar al t�rmino independiente (70) del segundo miembro, para lo cual se recurre a las propiedades de la igualdad.

x� + 3x - 70 = 70 - 70

x� + 3x - 70 = 0

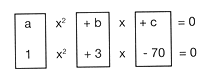
Obs�rvese la ecuaci�n con la forma general:

se aprecia que:

a = 1 (porque el coeficiente 1 no se escribe)

b = 3

c = - 70

esta apreciaci�n es �til porque existe una f�rmula general para resolver ecuaciones cuadr�ticas completas, que es la siguiente:

Para aplicar la f�rmula, se sustituyen las literales con los n�meros de la ecuaci�n y se realizan las operaciones indicadas, como se detalla en la siguiente p�gina:

entonces:

se extrae la ra�z cuadrada de 289

y se tiene:

como la ra�z (17) puede ser positiva o negativa, se consideran dos valores para x :

Es claro que -10 no puede ser la soluci�n del problema, porque la pista no puede medir -10 m de ancho o de largo. Por lo tanto, la soluci�n debe ser 7 m, ya que el valor de 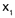es positivo.

As�:

Ancho = x = 7 m

Largo = x + 3m = l0m

�rea = largo x ancho = 10 m x 7 m = 70 m�

Esto comprueba que al resolver correctamente la ecuaci�n tambi�n fue acertada la soluci�n del problema.

V�anse los siguientes ejemplos:

a) 2x� - 5x - 33 = 0

F�rmula :

a = 2

b= -5

c= -33

Sustituyendo en la f�rmula:

Al realizar las operaciones indicadas:

- (-5) = 5

(-5)� = 25

(-4)(2)(-33) = -8(-33) = 264

2(2) = 4

se extrae la ra�z cuadrada de 289

entonces queda:

Como la ra�z de 289(17), puede ser positiva o negativa, se procede a obtener los dos valores de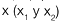

Comprobaci�n:

2x� - 5x - 33 = 0

b) 3x� - 2x - 8 = 0

F�rmula :

a = 3; b = -2; c = -8

Sustituyendo en la f�rmula:

Al realizar las operaciones indicadas:

- (-2) = 2

(-2)� = 4

-4(3)(-8) = -12(-8) = 96

2(3) = 6

se extrae la ra�z cuadrada de 100.

entonces queda:

Como la ra�z de 100(10), puede ser positiva o negativa, se procede a obtener los dos valores de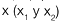

Comprobaci�n:

3x� - 2x - 8 = 0

La resoluci�n de ecuaciones cuadr�ticas completas se aplica para resolver una infinidad de problemas. Por lo tanto, es conveniente adquirir habilidad para plantear�as y resolverlas correctamente.