13. Semejanza de tri�ngulos

Corresponde a la sesi�n de GA 2.13 TE PARECES TANTO A MI

�Te pareces tanto a m�!. Regularmente, esta expresi�n se escucha en aquellas personas que observan en sus descendientes ciertos rasgos f�sicos que son muy similares a los suyos.

En geometr�a, existen casos en los que se presentan ciertas similitudes entre figuras; aqu� los conceptos de congruencia o semejanza se establecen cuando las figuras son de la misma forma y tienen igual o diferente tama�o.

En la congruencia, los lados y los �ngulos tienen la misma medida y, en la semejanza, las dos figuras tienen la misma forma, aunque no tengan necesariamente la misma medida o tama�o; sus �ngulos correspondientes u hom�logos deben ser congruentes y los segmentos correspondientes o lados hom�logos deben guardar entre s� una relaci�n proporcional.

�Cu�ndo se puede afirmar que dos tri�ngulos son semejantes? Para contestar esta pregunta es necesario que se cumplan las condiciones que se analizar�n a continuaci�n:

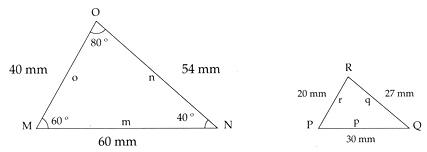
Obs�rvense los siguientes tri�ngulos: �ser�n semejantes?

Si se toma con un transportador la medida del �ngulo M, se puede ver que es congruente con el �ngulo P; de la misma forma, el �ngulo N es igual a Q, y R a O, por lo que se puede establecer que:

<M = <P = 60�; <N = <Q = 40�; <O = R=80�

Por otra parte, las medidas en mil�metros de los lados opuestos a estos �ngulos tienen una raz�n o constante de semejanza, esto es, el cociente de los lados opuestos a �ngulos iguales es constante.

Para comprobar que los �ngulos M, N y O del 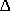MNO son, respectivamente, congruentes a los �ngulos P, Q y R del 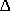PQR, se puede calcar el PQR, recortar y sobreponer, uno a uno, los �ngulos de los dos tri�ngulos,

como se ilustra a continuaci�n.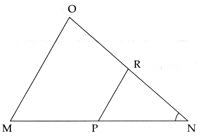

Gracias a los datos obtenidos puede afirmarse que los tri�ngulos MNO y PQR son semejantes. El s�mbolo ~ indica semejanza entre dos figuras, por lo que se pueden representar como:

Con base en las caracter�sticas se�aladas en el ejemplo anterior, se puede definir lo que es la semejanza entre tri�ngulos.

Dos tri�ngulos son semejantes si sus �ngulos son iguales uno a uno, respectivamente; los lados opuestos a dichos �ngulos son proporcionales.

En los tri�ngulos semejantes, los �ngulos congruentes y los lados proporcionales reciben el nombre de hom�logos.

Para determinar la semejanza entre dos tri�ngulos existen tres criterios que son los siguientes:

Primer criterio: �ngulo - �ngulo (a, a)

Dos tri�ngulos son semejantes si tienen dos de sus �ngulos respectivamente iguales.

Ejemplo:

Si se dice que:

Si se traslada la medida de DE al segmento AB desde el punto A, se encuentra el punto G. Desde ese punto se traza una paralela al segmento BC para encontrar en AC el punto H.

Los �ngulos ABC y AGH son congruentes por ser correspondientes entre paralelas, con lo que se tiene que:

Por lo tanto

Como los tres �ngulos del 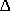ABC son congruentes con los �ngulos del 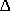DEF, por definici�n de semejanza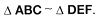

Por el teorema de Tales se sabe que una recta paralela a uno de sus lados determina segmentos proporcionales.

Por lo que:

Por ello se afirma que dos tri�ngulos son semejantes si tienen dos �ngulos congruentes.

Segundo criterio: lado - �ngulo- lado ( l, a, l )

Dos tri�ngulos son semejantes si dos de sus lados son proporcionales respectivamente y congruente el �ngulo que forman.

Ejemplo:

Tr�cese un tri�ngulo semejante a �ste con una constante de proporcionalidad de .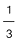

Se toma la medida del �ngulo M y se traza un �ngulo igual con v�rtice en R.

Para encontrar la medida del segmento RS se establece la proporci�n

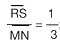como se conoce la medida de MN (6cm), se sustituye ese valor

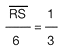con ayuda de la ley fundamental de las proporciones. De esa manera se encuentra la medida de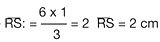

Para encontrar la medida del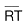, se establece otra proporci�n.

Como el criterio 2 ( l, a, l ) se�ala que, con dos lados proporcionales y siendo congruente el �ngulo comprendido, se puede establecer la semejanza entre dos tri�ngulos, entonces:

Tercer criterio: lado - lado - lado ( l, l, l )

Dos tri�ngulos son semejantes si sus tres lados son respectivamente proporcionales.

Ejemplo:

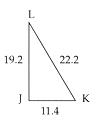
Dado el tri�ngulo GHI, construir un tri�ngulo JKL semejante a �l, sabiendo que la raz�n de semejanza o constante de proporcionalidad es de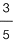

De acuerdo con el tercer criterio se afirma que:

Se sustituyen en cada una de las razones las medidas (en mil�metros) de los segmentos:

Con las medidas de 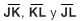se construye el tri�ngulo JKL, el cual, de con el criterio 3 (l, l, l) de congruencia, es semejante al GHI.