14. Teorema de Tales

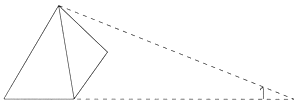
Corresponde a la sesi�n de GA 2.14 BUENA TRIANGULACI�N

El fil�sofo y matem�tico griego Tales de Mileto fue uno de los siete sabios m�s grandes de la antig�edad.

El teorema de Tales, llamado as� en su memoria, es una parte fundamental en el estudio de la semejanza. A �l se debe una de las numerosas aplicaciones que tiene la semejanza, que es la determinaci�n de la distancia entre dos puntos inaccesibles entre s�; para ello se dice que calcul� la altura de una de las pir�mides de Egipto sin medirla directamente, bas�ndose en la longitud de la sombra de su bast�n; as� logr� realizar una brillante triangulaci�n

El teorema de Tales afirma:

Si tres o m�s paralelas son cortadas por transversales, la raz�n entre las medidas de dos segmentos cualesquiera cortados por una transversal ser� igual a la raz�n de las medidas de los segmentos correspondientes de la otra, es decir, son proporcionales.

Al trazar el �ngulo TOS y dividir la recta OT en tres segmentos en donde cada divisi�n se marca con los puntos P, Q y R, si se trazan paralelas que corten a OT y OS por lo puntos P, Q y R, se originan los puntos U, V, W.

En la figura las medidas de los segmentos son las siguientes:

OP=2cm; PQ=2.5cm; QR=3cm

OU=3cm; UV=3.75cm; V W=4.5cm

Al establecer proporciones con las medidas, se observa que:

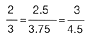es decir que las medidas de los segmentos correspondientes, son proporcionales.

En esta otra figura, al medir los segmentos MN, MN' NP y NP', se puede observar que las medidas son proporcionales:

al comprobar que los segmentos son proporcionales, se puede afirmar que las rectas NN' y PP' son paralelas. As� que:

Si una recta intriseca a dos lados de un tri�ngulo, y los divide proporcionalmente, entonces la recta es paralela al tercer lado.

Como consecuencia del teorema de Tales, se puede enunciar el teorema fundamental de semejanza de tri�ngulos.

Toda paralela a uno de los lados de un tri�ngulo, divide a los otros dos en segmentos proporcionales, por lo que forman un tri�ngulo semejante al primero.

Obs�rvese el tri�ngulo PQR, al trazar la recta TS paralela al lado RP se puede demostrar que:

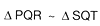por tener los lados proporcionales y los �ngulos hom�logos congruentes.

RP II TS

El �ngulo Q es com�n a los dos tri�ngulos

Los tri�ngulos PQR y SQT tienen �ngulos congruentes.

Adem�s:

por el teorema de Tales

Para obtener la proporcionalidad entre los segmentos, se traza la recta VS, paralela a RQ.

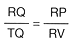Pero en el paralelogramo STRV, RV = TS. Se puede sustituir:

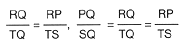as� que los lados de los tri�ngulos PQR y SQT son proporcionales

Por lo tanto 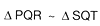porque sus �ngulos correspondientes son congruentes y sus lados hom�logos proporcionales.