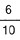ya que son 6 los que hay con m�sica en espa�ol.
Corresponde a la sesi�n de GA 2.20 CON UNA CONDICI�N
El estudio de la probabilidad ha adquirido auge en la actualidad, debido a la gran difusi�n que se les ha dado a los juegos de azar.
As�, se han realizado estudios sobre diversos aspectos y variantes de la probabilidad.
Anal�cese la siguiente situaci�n:
Juan y Carlos tienen en una caja 10 casetes, de los cuales 6 son de canciones en espa�ol y los restantes de canciones en ingl�s. Si van a escuchar algunos de ellos, �cu�l es la probabilidad de que al sacar tres al azar, uno tras otro, �stos sean de m�sica en espa�ol?
De aqu� se tiene que el total de casetes es de 10.
Los casetes de m�sica en espa�ol son 6.
Los casetes de m�sica en ingl�s son 4.
La probabilidad de que el primer casete sea de m�sica en espa�ol es de 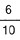ya que son 6 los que hay con m�sica en espa�ol.
La probabilidad de que el segundo casete sea de m�sica en espa�ol es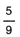 
esto es, 5 casetes que todav�a hay en la caja de m�sica en espa�ol y nueve en total, puesto que ya se sac� uno de ellos.
Ahora, en el tercer intento, la probabilidad de que el casete tambi�n sea de m�sica en espa�ol es de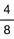 
; entonces, la probabilidad de sacar los tres casesetes de m�sica en espa�ol se determina multiplicando las probabilidades obtenidas.
Retomando el mismo problema, �cu�l ser� la probabilidad de que los tres casetes que saquen al azar sean de misma m�sica en ingl�s?
La probabilidad del primer casete es de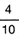 
la del segundo es de 
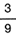y la del tercero es de 
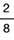; ahora la probabilidad se determina multiplicando las probabilidades obtenidas, esto es:
Obs�rvese que en este experimento no hay remplazo, raz�n por la cual la probabilidad en cada situaci�n es diferente; si el experimento se hubiera realizado con remplazo la probabilidad de todos los eventos hubiera sido la misma.
En un caj�n hay 5 expedientes de ni�os y 7 expedientes de ni�as. Si se van a extraer al azar, uno tras otro, �cu�l es la probabilidad de sacar los de las ni�as?
La probabilidad de que el primer expediente sea de una ni�a es de,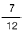 
puesto que son siete los expedientes de ni�a y 12 el total que hay en el caj�n.
Como no se regresa este expediente (no hay remplazo), la probabilidad de que el segundo sea de ni�a es de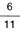 
, o sea, que hay 6 expedientes de ni�a de los 11 que quedan en el caj�n.
Para el tercer expediente, la probabilidad de que sea de ni�a es de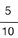 
; esto es, que s�lo quedan ahora 10 expedientes, de los cuales 5 son de ni�a.
La probabilidad de que los tres primeros sean de ni�a se obtiene multiplicando las tres probabilidades obtenidas:
De esta manera se puede calcular la probabilidad dada una condici�n.
![[ Índice Conceptos Básicos ]](toc.gif)
![[ Previo ]](prevsec.gif)
![[ Nivel Superior ]](parntsec.gif)
![[ Siguiente ]](nextsec.gif)
