19. Crecimiento aritm�tico y exponencial

Corresponde a la sesi�n de GA 2.19 LENTO Y R�PIDO

La poblaci�n, la reproducci�n de una bacteria, los r�ditos de un capital en el banco son ejemplos de cantidades que aumentan. Algunos de esos aumentos obedecen a una regla determinada.

Los crecimientos aritm�ticos y geom�tricos se�alan dos tipos diferentes de incrementos que puede sufrir una cantidad, aplicables a diversas actividades.

Crecimiento aritm�tico

Para comprar un libro que cuesta $ 75.00, Juan y Mart�n decidieron ahorrar desde el primer d�a $ 15.00 diarios, hasta que reunieran el dinero. �Cu�nto reunir�an el primero, segundo, tercero, y cuarto d�as? �En cu�nto tiempo tendr�an reunido todo el dinero? Para saberlo se auxiliaron de una progresi�n, donde anotaron lo que se acumular�a diariamente:

Con lo cual se observa que para el quinto d�a ya estar�a reunido el dinero, pues el t�rmino cinco de la progresi�n corresponde a la cantidad buscada.

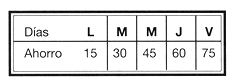
Esta variaci�n se puede se�alar en una tabulaci�n:

Se puede notar que el crecimiento diario es una cantidad constante en este caso: 15, al cual se le llama incremento.

Observe en la tabla que al sumar el dinero ahorrado y el incremento se obtiene el valor del siguiente t�rmino.

Este crecimiento se puede graficar:

A esta progresi�n se le da el nombre de crecimiento aritm�tico y su gr�fica es una l�nea recta.

Se le llama crecimiento aritm�tico a la progresi�n cuyos t�rminos aumentan por adici�n en una cantidad constante llamada raz�n.

En el ejemplo anterior la raz�n es +15.

La progresi�n puede ser creciente, si la raz�n es positiva, y decreciente si es negativa.

Ejemplo:

2, 4, 6, 8, 10 . Su raz�n es +2, por lo tanto es creciente.

24, 21, 18, 15, 12. Su raz�n es -3, por lo tanto es decreciente.

Crecimiento exponencial o geom�trico

Narra un viejo cuento que un monarca a quien le gustaba mucho jugar ajedrez dijo a Sissa, creador del juego, que le conceder�a lo que pidiera.

La petici�n de Sissa fue un grano de trigo por la primera casilla del tablero, dos por la segunda, cuatro por la tercera y as� sucesivamente, hasta la casilla 64.

Esto pareci� algo modesto y, sin embargo, no alcanzaron un pu�o de trigo ni un gran plato, tampoco un costal, ni siquiera toda la producci�n de trigo de la regi�n. As� que el monarca no pudo cumplir su palabra. �Cu�l fue el problema?

Se puede se�alar este ejercicio por medio de un diagrama.

Esta progresi�n se puede continuar. Num�ricamente ser�a:

1, 2, 4, 8, 16, 32...

y podr�a continuar hasta encontrar el t�rmino 64 con que finaliza la progresi�n.

Si se busca la relaci�n de cada uno de los t�rminos de la progresi�n se observa que cada elemento es el doble del anterior, por lo tanto su raz�n es 2.

La tabulaci�n de la progresi�n anterior ser�a la siguiente:

Su grafica ser�a:

La cual, como se observa, es una curva.

Este tipo de progresi�n recibe el nombre de crecimiento exponencial o geom�trico.

Se le llama crecimiento exponencial o geom�trico a aquella progresi�n que aumenta por multiplicaci�n de una cantidad constante llamada raz�n.

Cuando la raz�n de una progresi�n exponencial es mayor que uno, se dice que la progresi�n es creciente; si la raz�n es menor que uno la progresi�n es decreciente.

Ejemplos:

3, 9, 27, 81, 243. Creciente, pues su raz�n es 3

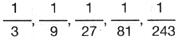. Decreciente. pues su raz�n es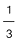

Los crecimientos ayudan a calcular el incremento de alguna cantidad en situaciones determinadas y tiene aplicaciones en �reas como f�sica, econom�a y biolog�a, entre otras.