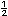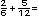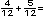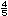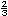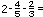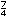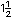|
|
|
Secuencia�9Matem�ticas I |
|
|
Problemas aditivos de n�meros fraccionarios y decimales |
| En esta secuencia resolver�s problemas aditivos con n�meros fraccionarios y decimales en distintos contextos |
Sesi�n 1
EL FESTIVAL DE FIN DE CURSOS
>>>Para empezar
 |
�D�nde se utilizan las fracciones? |
 |
En ocasiones las medidas de los materiales que se utilizan en la carpinter�a est�n expresados en fracciones. Por ejemplo, el grosor de las tablas y de las brocas y la longitud de los clavos se miden en pulgadas y fracciones de pulgada. |
>>>Consideremos lo siguiente
 |
En una telesecundaria se va a realizar el festival de fin de cursos y requieren construir un templete con una base de madera que tenga un grosor de una pulgada. La escuela s�lo cuenta con dos piezas de madera, una de media pulgada y otra de un tercio de pulgada. |
Si se empalman estas dos piezas, �su grosor ser� suficiente? __________
�Cu�nto faltar�a o sobrar�a? ___________________________________
 |
>>>Manos a la obra
-
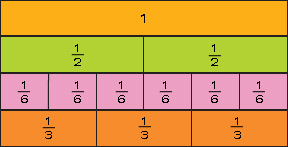
I. Utilicen el diagrama para encontrar la suma de media pulgada m�s un tercio de pulgada.
 |
-
a) Al empalmar las tablas, �cu�l es su grosor?________________ -
b) �Cu�nto falta para alcanzar el grosor de la base del templete que se requiere construir? __________________________________
-
II. Contesten en sus cuadernos.
-
a) Si las medidas del grosor de las tablas de madera fueran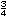 
de pulgada y
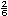de pulgada, �creen que se obtendr� el espesor
deseado para construir la base del templete? �Cu�l ser�a su grosor? Pueden
hacer un diagrama para calcularlo. �Cu�nto faltar�a o sobrar�a para alcanzar el
grosor de la base del templete?
| Recuerden que:
Para sumar o restar fracciones con diferente denominador se requiere convertirlas a fracciones equivalentes con igual denominador. |
-
b) �Qu� fracciones equivalentes utilizaron para calcular el grosor de las tablas de 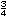y
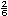de pulgada? -
c) Si las medidas del grosor de las tablas fueran: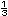 
de pulgada y
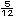de pulgada, al empalmarlas, �cu�l ser�a su
grosor? �Cu�nto faltar�a o sobrar�a para alcanzar el grosor de la base del
templete? -
d) �Qu� fracciones equivalentes utilizaron para calcular el grosor de las tablas de 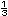y
? -
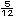e) �Cu�l de las siguientes operaciones con fracciones equivalentes consideran que es mejor para calcular la suma de 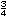y
?
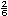| Primer caso | Segundo caso | |
 |
 |
-
f) En cada caso, �c�mo se obtienen esas fracciones? Si efect�an las operaciones, �obtienen el mismo resultado?
-
III. A continuaci�n aparecen tres opciones de empalmar dos tablas.
-
a) �Cu�l se acerca m�s a la medida deseada de una pulgada? Expliquen su respuesta y los procedimientos que siguieron para resolverlas.
|
-
b) �Cu�l de la siguientes opciones consideras que es mejor para calcular el grosor de las tablas de 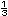y
?
|
|
||||
 |
-
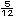a)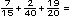 
-
b) 
-
c)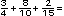 
-
V. Consideren que se quiere formar la base del templete con tablas cuyos grosores se se�alan en cada uno de los renglones del siguiente cuadro. �Qu� medida debe tener el grosor de la tercera tabla para construir la base del templete?
| Medida del
grosor de la
base del templete (en pulgadas) |
Grosor de la
primera tabla (en pulgadas) |
Grosor de la
segunda tabla (en pulgadas) |
Grosor de la
tercera tabla
(en pulgadas) |
|||
| 2 |
|
|
|
|||
| 3 |
|
 |
||||
|
|
|
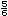>>>A lo que llegamos
| Para sumar o restar dos o m�s fracciones que tienen diferente denominador se deben obtener fracciones equivalentes con denominador com�n. | ||
|
||
Por ejemplo, en el
siguiente caso:
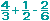 el denominador com�n de 2, 3 y 6 es 6. Al
expresar la operaci�n anterior con fracciones equivalentes con igual
denominador se obtiene: |
||
|
||
|
||
Por ejemplo, para la suma
 un denominador com�n se puede obtener
multiplicando los denominadores: 4 � 5 = 20. No hay que olvidar multiplicar
tambi�n los numeradores. Las fracciones equivalentes que se obtienen
son: |
||
|
||
Entonces, la suma queda
expresada como:
|
||
| Si en vez de sumarse estas fracciones se restaran, la expresi�n y diferencia ser�a: | ||
|
>>>Lo que aprendimos
 |
|
||
|
-
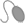a) 
-
b)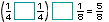 
-
c) 
|
|
-
a)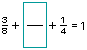 
-
b) 