Propósito de la sesión. Dar sentido a lo que significa dividir entre un número con punto decimal, descubrir que el cociente no siempre es mayor que el dividendo y que hay varias maneras de resolver algunas divisiones entre números decimales. Organización del grupo. Se sugiere trabajar en parejas durante toda la sesión, con algunos momentos de confrontación grupal.

Eje

Sentido numérico y pensamiento algebraico.

Tema

Significado y uso de los números.

Antecedentes

Los alumnos aprendieron en la escuela primaria a resolver divisiones: -en las que dividendo y divisor son naturales, hallando el cociente hasta centésimos; y -en las que el dividendo tiene cifras decimales. En esta secuencia los alumnos aprenderán a resolver divisiones en las que el dividendo y/o el divisor tengan cifras decimales.

Propósitos de la secuencia Resolver problemas que impliquen la división de números decimales en distintos contextos.
Sesión	Título y propósitos de la sesión	Recursos
1	El metrobús Dar sentido a lo que significa dividir entre un número con punto decimal, descubrir que el cociente no siempre es mayor que el dividendo y que hay varias maneras de resolver algunas divisiones entre números decimales.	Video "El metrobús" Interactivo "División de números decimales"
2	Cambio de dinero Conocer y practicar la técnica para dividir entre un número con punto decimal.
3	Números decimales en la ciencia Resolver diversos problemas que implican operaciones de números con punto decimal.

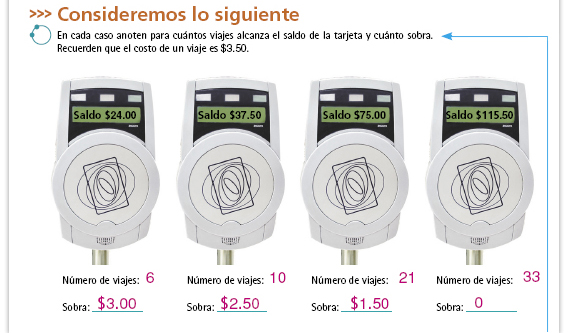
Propósito de la actividad. La finalidad es que los alumnos interpreten la división como la operación que permite saber cuántas veces cabe un número en otro. En este caso, deberán calcular "cuántas veces cabe" el número 3.50 en cada una de las cantidades indicadas como saldo. Es importante que en este momento los alumnos no utilicen la calculadora para que puedan hacer uso de otras estrategias. Posibles procedimientos. -Sumar varias veces 3.50 hasta llegar al número más cercano al saldo indicado. -Restar 3.50 al saldo indicado las veces que sea necesario hasta agotarlo o hasta que ya no alcance el dinero para un viaje más. -Multiplicar 3.50 por diferentes números hasta obtener un producto que se aproxime al saldo indicado. -Dividir el saldo entre 3.50. Sugerencia didáctica. Mientras las parejas resuelven, trate de identificar qué procedimientos utilizan para, posteriormente, recuperar algunos de ellos durante la confrontación.

Sugerencia didáctica. Es importante que el algoritmo de la división sea considerado como una manera más de resolver el problema, no es la única y no siempre la mejor; por ejemplo, si el saldo es $37.50 se puede calcular más rápidamente sabiendo que de 10 viajes son $35.00 y sobra $2.50.

Propósito de la actividad. Se pretende que los alumnos identifiquen que la actividad que resolvieron en la sección Consideremos lo siguiente puede solucionarse mediante una división. Por eso es importante que utilicen los datos que encontraron anteriormente para completar la tabla.

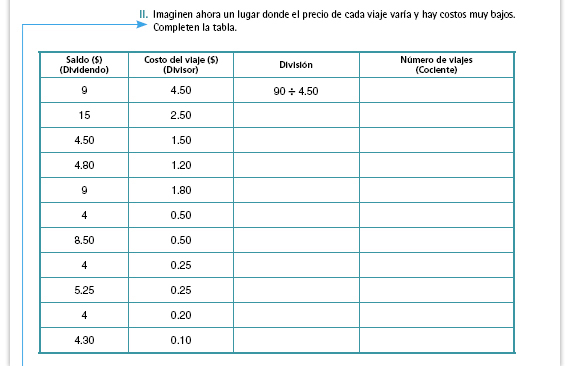
Sugerencia didáctica. Mientras las parejas resuelven, usted puede plantear algunas preguntas para que los alumnos vayan reflexionando sobre aspectos interesantes que revisarán en las siguientes actividades; por ejemplo, para que identifiquen cómo varía el cociente en función del divisor: si el saldo es de $4 ¿a cuál destino se puede ir más veces, a uno cuyo viaje cuesta $0.50 o a otro que cuesta $0.20? Posibles procedimientos. Los alumnos podrían ir completando cantidades "redondas": si el costo del viaje es de $2.50, con $5.00 se hacen 2 viajes; si el costo es de $0.20, con $1.00, se hacen 5 viajes. También pueden recurrir al cálculo mental para resolver varias de las divisiones, pues los números que se ponen en juego son relativamente sencillos de manejar. Invite a los alumnos a que completen la tabla utilizando los procedimientos que ellos quieran; en este momento no es necesario que todos usen el algoritmo de la división, aunque sí es importante que sepan que están resolviendo divisiones. Recuerde que.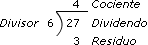

Propósito de la actividad. Hay dos aspectos interesantes que los alumnos trabajan: -Reconocer que al dividir no siempre el cociente resulta menor que el dividendo; por ejemplo, al dividir 4 entre 0.50 el resultado es 8 (8 > 4). -Al analizar en qué casos el cociente es mayor o menor que el dividendo, los alumnos podrán desarrollar, gradualmente, estrategias para estimar resultados. Respuestas a) Cuando el costo del viaje (divisor) es mayor que uno. b) Cuando el costo del viaje (divisor) es menor que uno.

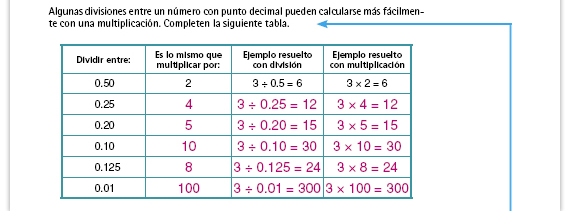
Propósito de la actividad. Que los alumnos se den cuenta de que el resultado de una división también puede obtenerse multiplicando por el inverso del divisor. Por ejemplo, para hallar el resultado de dividir 4 ÷ 0.1 se puede también multiplicar 4 × 10. En algunos casos, una manera es más sencilla que otra, y se espera que los alumnos vayan adquiriendo habilidades para decidir cuál les conviene, dependiendo de las circunstancias. Este tipo de prácticas son muy importantes porque desarrollan el sentido numérico de los alumnos. Sugerencia didáctica. Invite a los alumnos a que multipliquen los números de la primera y segunda columnas. Por ejemplo, 0.5 × 2; 0.25 × 4; 0.125 x 8. En todos los casos se obtiene 1. Pregunte: ¿Por qué creen que sucede esto? Integrar al portafolios. Recupere esta actividad y analice las respuestas de los alumnos. Si lo considera necesario, revisen la secuencia 11, en ella se llena una tabla en la que se observa que dividir una fracción es lo mismo que multiplicarla por su recíproco.

Sugerencia didáctica. El cálculo mental es una herramienta que permite, además de obtener algunos resultados de manera rápida, desarrollar habilidades, como establecer relaciones entre los datos y anticipar resultados. Invite a los alumnos a que resuelvan mentalmente estas operaciones, se darán cuenta de lo eficaz que es este tipo de cálculo y de las múltiples relaciones que pueden darse entre los números.

Propósito del interactivo: Mostrar gráficamente la división de decimales por medio de la idea "cuántas veces cabe en".

Sugerencia didáctica. Pida a los alumnos que escriban en su cuaderno dos ejemplos diferentes a los que se plantean en el recuadro de cada uno de los puntos.

Propósito del video. Observar el planteamiento y la solución de problemas que involucren la división entre un número decimal. Observar qué sucede cuando se divide entre un número menor o mayor que la unidad.