Propósito de la sesión. Conocer y practicar la técnica para dividir entre un número con punto decimal. Organización del grupo. Inicie la sesión trabajando con el grupo en conjunto; posteriormente organice parejas para resolver la sección Consideremos lo siguiente.

Sugerencia didáctica. Dé tiempo para que los alumnos lean el apartado Para empezar y después comente con el grupo la información que se presenta. Repasen las divisiones con punto decimal en el dividendo resolviendo algunas en el pizarrón. Es necesario que los alumnos sepan resolver este tipo de divisiones para que puedan continuar con la sesión.

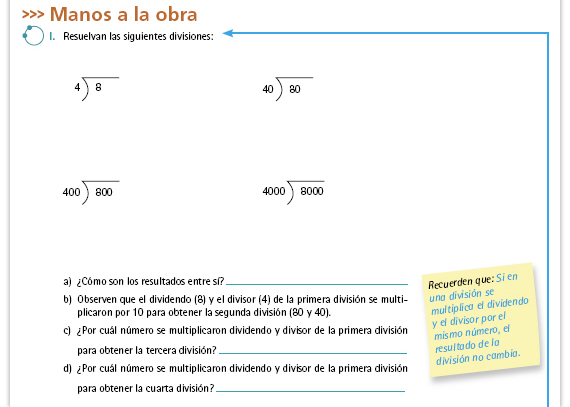
Sugerencia didáctica. Es probable que los alumnos no sepan cómo resolverlas. Invítelos a que lo intenten, recuerde que en estos momentos se trata de crear en los alumnos un conflicto al darse cuenta de que estas divisiones son distintas a las que ya conocen, así como la necesidad de hallar la manera de resolverlas. Propósito de la actividad. Se pretende que los alumnos manejen la técnica para dividir números con punto decimal. Por ello deberán resolver el problema utilizando una división y no mediante otros procedimientos (aunque sean correctos).

Sugerencia didáctica. Anime a los alumnos para que expliquen sus intentos y escuchen los de otros. En caso de que alguna pareja sí haya podido resolver la división, pida a sus integrantes que muestren al grupo cómo lo hicieron. Si nadie logró resolverla, invítelos a que continúen trabajando la sesión.

Sugerencia didáctica. Los alumnos ya estudiaron esta propiedad en la escuela primaria, por lo que la actividad puede ser considerada como un repaso; no obstante, usted puede enriquecerla comentando al grupo que, si se parte de que una división puede escribirse como fracción, al multiplicar dividendo y divisor por el mismo número, lo que se está haciendo es calcular fracciones equivalentes. Observe: Esto implica que: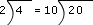

Sugerencia didáctica. Puede pedir a los alumnos que: 1.. Estimen el resultado antes de que pasen al inciso a). Por ejemplo, si está entre 1 y 10, entre 10 y 100 o entre 100 y  1 000. 2.. Calculen mentalmente el resultado antes de que pasen al inciso a). 3.. Resuelvan la división y verifiquen su resultado en la calculadora. 4.. Una vez resuelta, inventen un problema que se resuelva con esa operación. Si lo considera necesario, plantee más operaciones de este tipo para que los alumnos las resuelvan en su cuaderno.

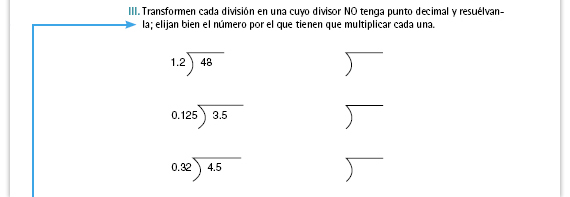
Respuestas. Se multiplica por 10, 480 ÷ 12 = 40 y no sobra. Se multiplica por 1 000, 3 500 ÷ 125 = 28 y no sobra. Se multiplica por 100, 450 ÷ 32 = 14 y sobra 2. Si algunos alumnos continúan dividiendo obtendrán 14.0625. Si lo considera pertinente, comente con sus alumnos lo que sucede con el residuo en esta división. Si bien es cierto que al multiplicar por un mismo número el dividendo y el divisor, el cociente no se altera, no pasa lo mismo con el residuo. Éste aumenta tantas veces como el número por el cual se multiplicó. Por ejemplo, mientras que en la división original (4.5 ÷ 0.32) el residuo es 0.02, en la división transformada (450 ÷ 32) el residuo es 2. El residuo de la división transformada es 100 veces mayor que el de la división original.

Propósito de la actividad. Esta actividad permite que los alumnos validen el resultado que obtuvieron en el problema inicial. Si es necesario pídales que corrijan. Puede haber discrepancia en los resultados si algunos alumnos dejaron el residuo y si otros continuaron la división. Es buen momento para que los anime a terminar la división.

Sugerencia didáctica. Resuelvan en el pizarrón más divisiones y aclare las posibles dudas.

Respuestas. Araceli tiene 100 monedas (50 ÷ 0.50). Necesita 5 monedas para hacer cada montón de $2.50, así que puede hacer 20 montones. Luis tiene 100 monedas (500 ÷ 5). Necesita 5 monedas para hacer cada montón de $25, así que también puede hacer 20 montones. Entonces la respuesta correcta es c).

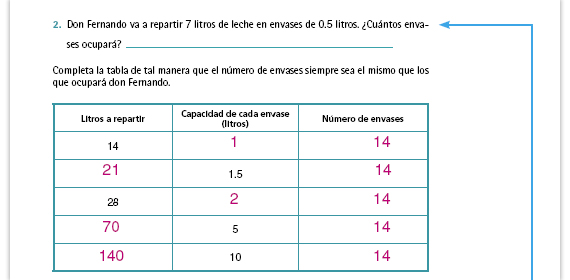
Respuestas. El número de envases siempre debe ser 14, entonces la cantidad de litros de leche a repartir hay que dividirla entre 14 para obtener la capacidad de cada envase. Si lo que conocemos es la capacidad de cada envase, entonces ese número se multiplica por 14 para hallar la cantidad de litros a repartir.

Respuestas. El resultado es 4.6 Se obtendría el mismo cociente con números como: 92 entre 20 920 entre 200 9 200 entre 2 000 92 000 entre 20 000 920 000 entre 200 000, etcétera.