
|

|

|
 |
 |

| Propósito de la sesión. Calcular las
probabilidades de diversos eventos
y distinguir entre ellos cuál es más
probable que ocurra, cuál es menos
probable y cuáles tienen la misma
probabilidad de ocurrir.
Organización del grupo. Se sugieren actividades individuales, en parejas y en equipos. |
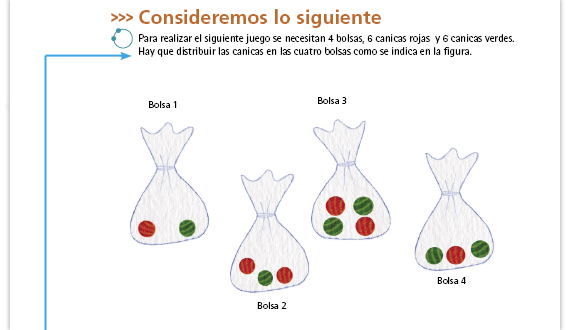
| Sugerencia didáctica. Si no tienen a la mano canicas pueden sustituirlas por papeles de colores o con el nombre del color escrito. |

 Propósito de las preguntas. Es muy
importante que los alumnos contesten
las preguntas antes de realizar el
experimento. Se pretende que al
responderlas hagan uso de lo que
han aprendido sobre la probabilidad
clásica, sin embargo, puede ser que en
un primer momento no se den cuenta
de que es igualmente probable
obtener una canica roja en la bolsa 1
y en la 3.
Propósito de las preguntas. Es muy
importante que los alumnos contesten
las preguntas antes de realizar el
experimento. Se pretende que al
responderlas hagan uso de lo que
han aprendido sobre la probabilidad
clásica, sin embargo, puede ser que en
un primer momento no se den cuenta
de que es igualmente probable
obtener una canica roja en la bolsa 1
y en la 3.
Respuestas. En la bolsa 1 la probabilidad es 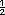 ,
y en la 3 es ,
y en la 3 es 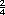 , es decir, en ambas
es igualmente probable extraer una
canica roja. , es decir, en ambas
es igualmente probable extraer una
canica roja.
Es mejor elegir la bolsa 2 porque ahí la probabilidad es 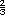 y es mayor que
en cualquiera de los otros casos. y es mayor que
en cualquiera de los otros casos. |
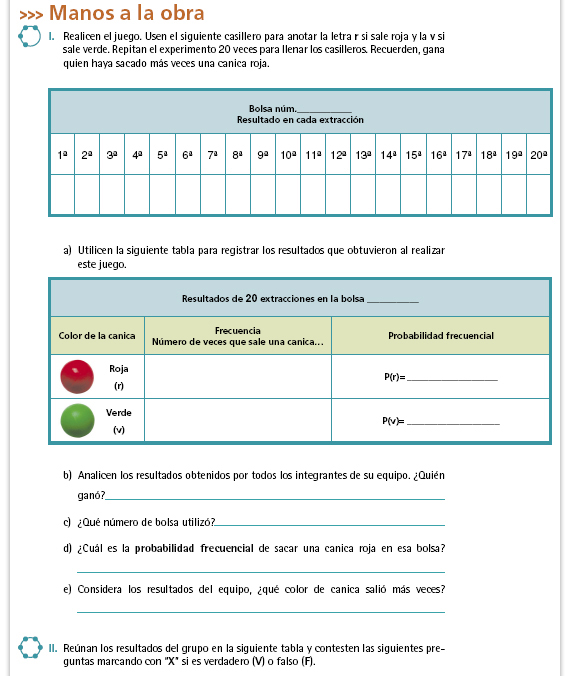
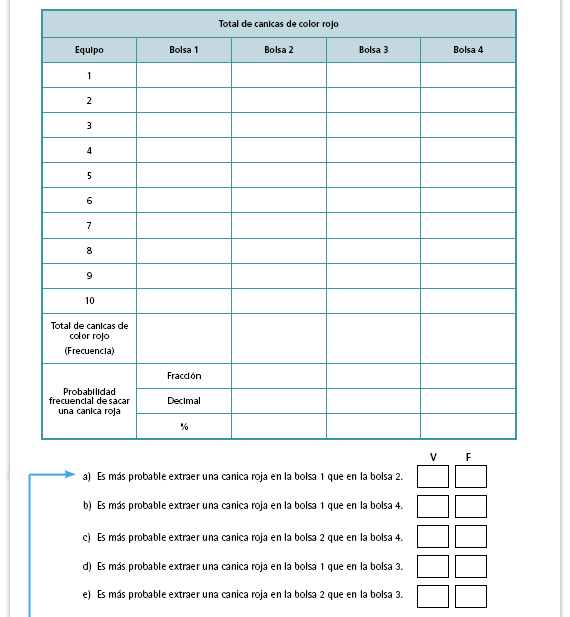
| Sugerencia didáctica. Para
responder estos incisos los alumnos
deben considerar los resultados de
sus experimentos que reunieron
en la tabla anterior. Cuando hayan
terminado, anote en el pizarrón los
incisos y contéstenlos considerando
ahora la probabilidad clásica.
Comparen ambas respuestas
y comenten sus diferencias y
coincidencias (si las hubo).
Considerando la probabilidad clásica, las respuestas serían:
|

| Respuestas. La probabilidad clásica
en cada bolsa es:
Bolsa 1 y bolsa 3: 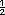 . .
Bolsa 2: 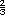 . .
Bolsa 4: 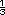 . .
Sugerencia didáctica. Es posible que en la bolsa 3 algunos alumnos escriban 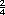 . Señale que, como . Señale que, como
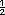 y y 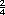 son equivalentes, la probabilidad en
ambas bolsas es la misma.
son equivalentes, la probabilidad en
ambas bolsas es la misma. |

| Sugerencia didáctica. Cuando contesten estas preguntas, pida a los alumnos que revisen lo que respondieron en la sección Consideremos lo siguiente y que corrijan si es necesario. |