Propósito del video. Identificar y visualizar situaciones en las que obtienen la probabilidad frecuencial y en qué situaciones obtienen la probabilidad clásica.

Propósito de la sesión. Explorar y analizar la relación entre la probabilidad frecuencial y la clásica. Organización del grupo. Hay momentos de resolución individual, en parejas y en equipos.

Propósito de las preguntas. La intención es que los alumnos se vayan familiarizando con el análisis de resultados posibles y con el cálculo de la probabilidad clásica y frecuencial.

Respuestas. a) 2, 4, 6, 8, 10. b) Hay cinco formas (sacando 2, 4, 6...). c) Es

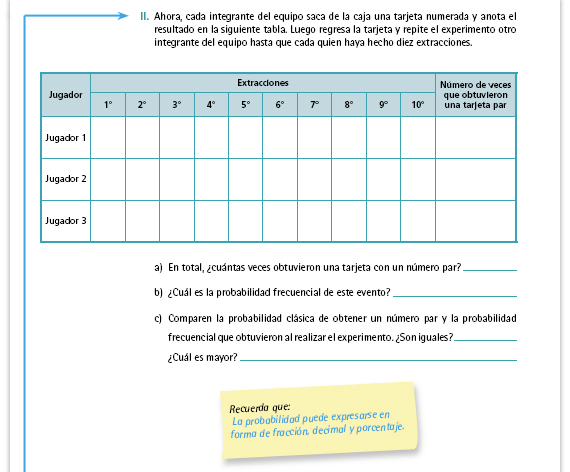
Sugerencia didáctica. Recuerde que es indispensable que los alumnos realicen todos los experimentos para poder lograr los propósitos de la sesión. Propósito de la actividad. Se pretende que los alumnos analicen las diferencias y coincidencias entre la probabilidad clásica y la frecuencial. En general, la probabilidad frecuencial y la clásica en este experimento no van a ser iguales (porque 10 extracciones son muy pocas para que la probabilidad frecuencial se acerque a la clásica). Cuando terminen de contestar las preguntas pídales que expliquen los resultados que obtuvieron y que expresen sus dudas (si las tienen), más adelante podrán aclararlas.

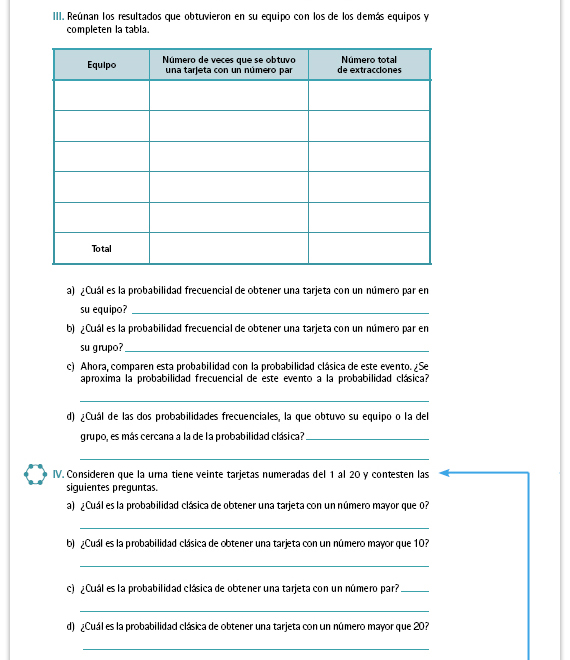
Respuestas. a) Es 1, un evento seguro. b) = c) = d) 0, es un evento imposible. e) No, un evento favorable debe "caber" en el número de eventos posibles.

Sugerencia didáctica. Lean esta información. Después revisen sus respuestas a los números II y III del Manos a la obra y aclaren dudas.

Respuestas. a) Clásica, no se realiza el experimento. b) Frecuencial, sí se lleva a cabo el experimento. c) Clásica, no se llevó a cabo.

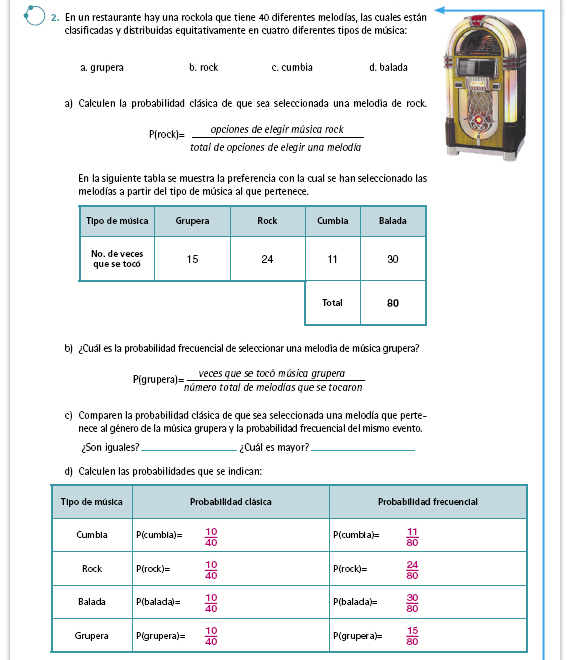
Propósito de la actividad. A diferencia de los anteriores, este experimento no es aleatorio porque no depende del azar sino de la preferencia de cada persona. Por ello, aunque muchas personas elijan en la rockola su música favorita, la probabilidad frecuencial no necesariamente tenderá a la clásica, que en este caso es 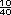o 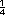. En esta actividad la intención es que el alumno identifique situaciones relacionadas con la preferencia (de música, candidatos, deportes, etc.) y la probabilidad; es decir, introducir la probabilidad y la estadística de un modo experimental, además de confrontar creencias personales o de carácter determinista con la importancia y utilidad de la estadística para la toma de decisiones con una base racional y objetiva. Respuestas. 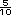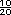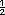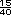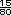a) Como están distribuidas equitativamente es b) c) No son iguales. Es mayor la probabilidad clásica ( > ).