Propósito de la sesión. Interpretar información numérica obtenida en diversas fuentes (encuestas, diarios, almanaques, etc.) utilizando en sus análisis indicadores de medidas de tendencia central, y decidir en qué casos es conveniente usar cada una para analizar la información. Organización del grupo. El trabajo es en parejas a lo largo de toda la sesión, excepto en la confrontación, que es grupal.

Sugerencia didáctica. Pida a los alumnos que piensen en otra situación en la que tomar una de las medidas de tendencia central no da una buena idea del comportamiento de los datos, o incluso da una idea equivocada. Por ejemplo, "Las estadísticas muestran que casi todos los accidentes de circulación se producen entre vehículos que circulan a velocidad moderada. Muy pocos ocurren a más de 110 km por hora". ¿Significa esto que resulta más seguro conducir a gran velocidad?

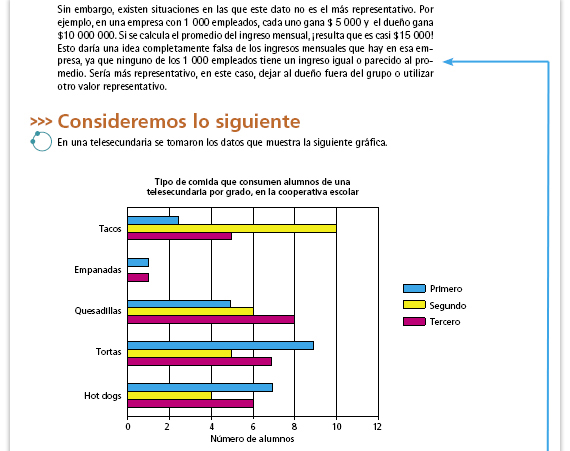
Respuestas. Tortas, 21 alumnos las consumieron. Posibles dificultades. Algunos alumnos pueden creer que el alimento que más se consume son tacos, porque en la gráfica tienen la barra más larga. Sin embargo, hay que tomar en cuenta que cada barra señala la preferencia de un grado por un alimento, así que para saber cuántos alumnos de toda la escuela escogieron cierta comida deben sumarse las frecuencias señaladas en las tres barras.

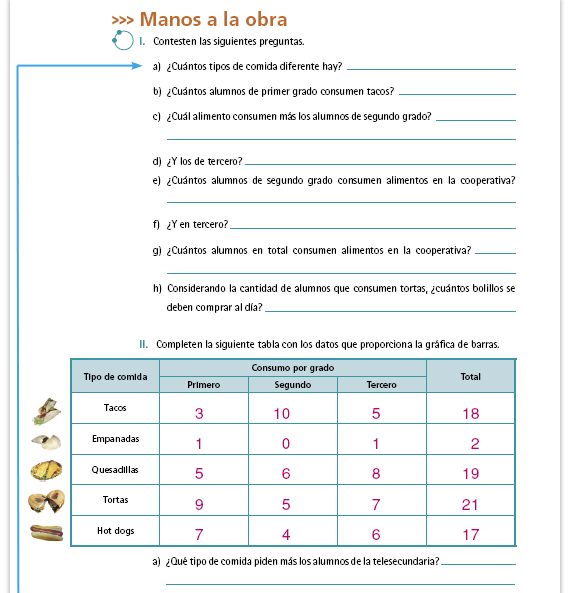
Respuestas. a) 5 (tacos, empanadas, quesadillas, tortas y hot dogs). b) 3 c) Tacos. d) Quesadillas. e) 25 f) 27 g) 77 h) 21 bolillos.

Respuestas. a) Tortas. b) 7 tortas. c) 6.3 quesadillas. d) Ninguna. e) o 0.67 redondeando. Sugerencia didáctica. Pregunte a los alumnos qué significa que el promedio de empanadas que se consumen por grado sea de 0.67.

Respuestas. a) $10 b) La mínima es $0, la máxima es $100, la diferencia es 100. c) $10 Recuerde que. Cuando se ordena un conjunto de datos para encontrar la mediana y se tienen casos como el siguiente: 4    6    22     28    29    70 no hay un dato que se encuentre justo a la mitad (quedaría entre el 22 y el 28). Lo que se hace en estos casos es sacar el promedio de los dos datos que quedan en medio (25), y el número obtenido se considera la mediana.

Respuestas. d) 10 f) La moda y la mediana. g) Los que gastan $100 hacen que el promedio suba mucho. 23 alumnos gastan menos de $15.

Respuesta. 65 puntos porque lleva 115 y necesita un total de 180.

Respuestas. 18 puntos porque entre la primera y la tercera tiene 72 y necesitó llegar a 90 para obtener un promedio de 30.

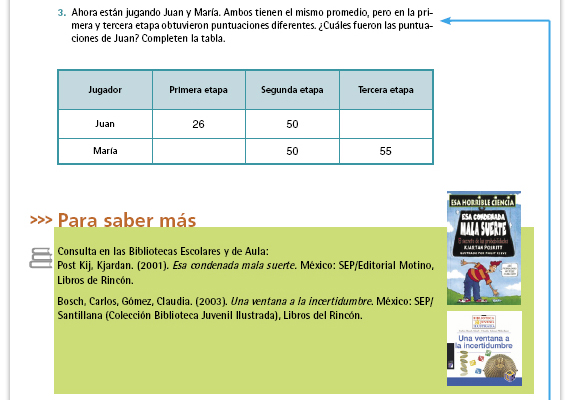
Posibles respuestas. La pregunta admite una infinidad de respuestas correctas. Para obtener 50 puntos de promedio tiene que sumar 150 puntos en las tres etapas, así que son válidos todos aquellos pares de números que den un total de 150 puntos (incluyendo los 50 que obtuvo en la segunda etapa) y que además, sean distintos de 45 en la primera etapa y 55 en la tercera (porque el problema dice que Juan obtuvo distintas puntuaciones que María).