Propósito de la sesión. Utilizar el significado de la moda, la media y la mediana para interpretar y comunicar información sobre un conjunto de datos. Organización del grupo. El trabajo es en parejas a lo largo de toda la sesión, excepto en la confrontación, que es grupal.

Eje

Manejo de la información.

Tema

Representación de la información.

Antecedentes

Desde la escuela primaria los alumnos han trabajado con las medidas de tendencia central en diversas situaciones. Ahora se pretende que además de calcularlas, las analicen a partir de gráficas ya elaboradas.

Propósitos de la secuencia Comparar el comportamiento de dos o más conjuntos de datos referidos a una misma situación o fenómeno a partir de sus medidas de tendencia central.
Sesión	Título y propósitos de la sesión	Recursos	Vínculos
1	Promedios Utilizar el significado de la moda, la media y la mediana para interpretar y comunicar información sobre un conjunto de datos.	Español I Secuencia 14
2	¿Qué prefieren comer? Interpretar información numérica obtenida en diversas fuentes (encuestas, diarios, almanaques, etc.) utilizando en sus análisis indicadores de medidas de tendencia central, y decidir en qué casos es conveniente usar cada una para analizar la información.

Propósito del video. Presentar diversas situaciones en las que tiene sentido la aplicación del promedio en su vida diaria.

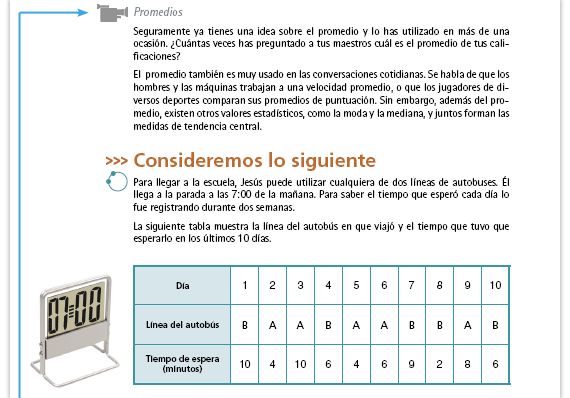
Propósito de la actividad. La intención de la pregunta es que los alumnos se den cuenta de que no es posible decir con exactitud cuánto tiempo tendrá que esperar el autobús, pero que pueden hacer una estimación basándose en los datos de la tabla. Posibles respuestas. Algo que los alumnos pueden notar al analizar la tabla es que el 6 se repite tres veces, es decir, que en tres de los diez días Jesús esperó 6 minutos, y por ello afirmar que es más probable que el onceavo día tenga que esperar 6 minutos. También pueden calcular el promedio de tiempo de espera. En total, esperó 65 minutos en los diez días, por lo tanto el promedio es de 6.5 minutos.

Respuestas. a) 2 minutos. b) 10 minutos. c) 6 minutos. d) 6.5 minutos. e) No.

Respuestas. a) 6 minutos. b) 8 minutos. c) La línea A, con 6.4 minutos.

Posibles respuestas. Los alumnos pueden considerar el promedio o la moda para contestar el inciso d). Pídales que expliquen por qué eligen una u otra.

Propósito de la pregunta. Se busca que los alumnos, además de calcular las medidas de tendencia central, conozcan algunas de sus características y significados; y que distingan en qué situaciones debe considerarse una u otra para comunicar cómo se comporta la información. Respuestas. a) 6 minutos. b) 6.9 minutos. c) La moda, porque un autobús excepcionalmente puede tardar mucho (lo que haría que el tiempo promedio de espera se elevara) y no reflejaría que la mayoría de las veces el tiempo de espera es menor. Integrar al portafolios. Recupere las respuestas de los alumnos a las preguntas de la actividad 1.