BLOQUE 2

Un candado muy seguro Uso de diagramas de árbol para encontrar el número de resultados posibles 1. Javier tiene un candado de seguridad y se le olvidó la combinación que lo abre. El candado tiene 3 cilindros y cada cilindro tiene los dígitos del 0 al 9; sólo hay una combinación de dígitos que permite abrir el candado ¿Cuántas combinaciones crees que tendrá que probar Javier? Organiza equipos de 3 o 4 compañeros y haz una estimación del número de combinaciones posibles en el candado. ¿Serán entre 10 y 100? ¿entre 100 y 200? ¿más de 200? 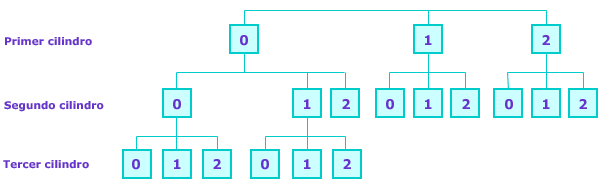¿más de 1 000?_____________________________ Para encontrar una estrategia que te permita calcular el número de combinaciones posibles del candado, puedes empezar con una situación más sencilla: supón que los cilindros del candado tienen solamente 3 cifras cada uno (el 0, el 1 y el 2). Un diagrama de árbol puede ayudarte a contar el número de combinaciones. Copia en tu cuaderno el siguiente y complétalo. Si Javier empieza con el 0 en el primer cilindro ¿cuántas combinaciones tendrá que probar?_________________________________________________ Enuméralas en tu cuaderno. ¿Y si empieza con el 1?_________________________________________ Enuméralas en tu cuaderno. ¿Y si empieza con el 2?_________________________________________ Enuméralas en tu cuaderno. ¿Cuántas son en total? _________________________________________ Enuméralas en tu cuaderno. ¿Puedes enunciar una regla para obtener el número de combinaciones si los cilindros del candado sólo tienen 3 cifras cada uno? ¿Cuál sería? __________________________________________________________ 2. Ahora supón que los cilindros del candado tienen 4 cifras (0, 1, 2, 3) cada uno. Haz en tu cuaderno un diagrama de árbol como el anterior para encontrar el número de combinaciones posibles. Recuerda que son 3 cilindros. Si Javier empieza con el 0 en el primer cilindro, ¿cuántas combinaciones tendrá que probar? Enuméralas en tu cuaderno. Si Javier empieza con el 1, ¿cuántas combinaciones tendrá que probar? Enuméralas en tu cuaderno. Si Javier empieza con el 2, ¿cuántas combinaciones tendrá que probar? Enuméralas en tu cuaderno. Si Javier empieza con el 3, ¿cuántas combinaciones tendrá que probar? Enuméralas en tu cuaderno. ¿Cuántas combinaciones son en total? Enuméralas en tu cuaderno. ¿Puedes enunciar una regla para obtener el número de combinaciones si los cilindros del candado sólo tienen 4 cifras cada uno? ¿cuál sería? __________________________________________________________ Ahora trata de enunciar una regla para calcular el número de combinaciones del candado de Javier. ____________________________________________ ¿Qué tan grande es el número resultante?___________________________ ¿Crees que el candado de Javier es seguro? _________________________ ¿Por qué?___________________________________________________ 3. Las compañías telefónicas hacen uso de este tipo de combinaciones para evitar que haya dos teléfonos con el mismo número. ¿Cuántos números telefónicos de 6 cifras se pueden formar con los dígitos del 0 al 9?______________________________________________________ ¿Se puede usar cualquiera de esas combinaciones?____________________ ¿Cuáles crees que se omiten?____________________________________ ¿Por qué crees que las compañías de teléfonos tienen que agregar una clave diferente para las distintas regiones del país?_________________________ __________________________________________________________ Contar el número de combinaciones posibles en una situación dada es una herramienta matemática muy importante. Los bancos, las compañías telefónicas y los sistemas de seguridad, usan códigos basados en estas combinaciones. Comenta con tus compañeros y tu maestro, en dónde más se usan las combinaciones de números o de letras o de ambos.