|

|

|

|
 |
 |
|||||||||
|
Los juegos de azar han fascinado al hombre desde las épocas más remotas. El dado más antiguo que se conoce, elaborado con arcilla y cubierto de cuero, data del año 3000 a.C. Sin embargo, el cálculo de la probabilidad, como una aplicación matemática, es mucho más reciente; a sus orígenes están asociados los nombres de dos grandes matemáticos del siglo xvii: Blaise Pascal (1623-1662) y Pierre Fermat (1601-1665). Se cuenta que un culto caballero, aficionado a los juegos de azar, pidió ayuda a Pascal para resolver el problema que hoy conocemos como de la división de la apuesta. Pascal, a su vez, propuso el problema a su amigo Fermat, los dos encontraron procedimientos diferentes, aunque ambos llegaban a la misma solución. El problema es el siguiente: Dos jugadores participan en un juego de azar en donde los dos tienen las mismas oportunidades de ganar (por ejemplo, un volado). El primero que gane 5 veces se lleva la totalidad de la apuesta. Desgraciadamente, la partida debe interrumpirse cuando uno de los jugadores ha ganado 4 juegos y el otro jugador ha ganado 3 juegos. ¿Cómo deben repartirse la apuesta? Si proponemos que la apuesta se divida en partes iguales, seguramente protestaría el jugador que ha ganado 4 veces, porque él tenía una ventaja en el momento de interrumpir la partida. Tampoco es aceptable la solución de dividir la apuesta proporcionalmente a 4 y 3, porque esta solución no depende del número total de juegos que deben ganarse (5) para llevarse la apuesta.
 + +
 de la apuesta y el jugador B
debe recibir de la apuesta y el jugador B
debe recibir
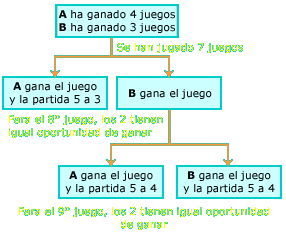
 de la apuesta. Esta solución puede ilustrarse con un
diagrama de árbol como el de la derecha. de la apuesta. Esta solución puede ilustrarse con un
diagrama de árbol como el de la derecha.
Resuelve el problema cuando los jugadores juegan a ganar 3 juegos con una apuesta de $1 000.00 y la partida se interrumpe cuando uno ha ganado 2 juegos y el otro, 1. |
|||||||||
 |

|

|

|
 |