 |

|

|

|
 |
 |
||||||||
|
Cuando contemplamos el cielo nocturno, tachonado de estrellas tenemos una experiencia muy cercana al infinito. Sentimos la inmensidad de nuestro Universo y la enorme cantidad de estrellas que existen en él. Al mismo tiempo, imaginamos nuestro planeta Tierra como un pequeñísimo grano de arena. Hay otros momentos más familiares en los que la noción de infinito nos hace sentir que caemos en un abismo: son las figuras que parecen repetirse sin límite. Por ejemplo, una figura que tiene dentro una figura igual a sí misma, que tiene dentro de sí una figura igual a sí misma, que tiene dentro una figura igual a sí misma, y así hasta el ...infinito. ¿Alguna vez te has visto en un espejo colocado frente a otro espejo? En uno se refleja la imagen del otro, que refleja la imagen del primero, que refleja la imagen del segundo... ¿serán infinitas las imágenes? En todos estos casos, la palabra infinito se usa como sinónimo de "sin fin", o "sin límite". En matemáticas, el infinito ha estado presente desde épocas muy remotas asociado tanto a lo muy muy grande como a lo muy muy pequeño, pero siempre estremeciendo la racionalidad del hombre y planteándole paradojas que, a veces, no puede resolver. A partir de la sucesión de los números naturales 1, 2, 3, 4, ..., ¿se puede pensar en un número que sea mayor que cualquiera? ¿será un millón? ¿un billón? ¿un trillón? No, porque para cada uno de estos números se puede encontrar siempre un número mayor, basta sumar 1 cada vez. ¡Hay un número infinitamente grande de números! Piensa en un segmento de recta de 1 metro de longitud; divídelo en 2 y quita una de las mitades, la otra, divídela en 2; ahora quita una de las mitades y divide en 2 la restante, continúa con esta operación, ¿qué crees que quede al final? La respuesta inmediata es "¡no queda nada!" pero, pensémosla un poco más despacio:
La primera mitad mide
No, porque al sumar las fracciones podemos constatar que
este resultado es casi 0.001 metro que, aunque ciertamente es
muy pequeño ¡es diferente de cero! Si repitiéramos 100 veces el mismo
procedimiento, quedaría
|
||||||||
 |

|

|

|
 |



 metro, si la dividimos en dos, en la segunda etapa nos
quedará
metro, si la dividimos en dos, en la segunda etapa nos
quedará
 de metro; en la tercera etapa, tendremos la mitad de
de metro; en la tercera etapa, tendremos la mitad de
 de metro; en la cuarta etapa nos quedará
de metro; en la cuarta etapa nos quedará
 de metro; en la quinta,
de metro; en la quinta,
 ; en la sexta,
; en la sexta,
 ; en la séptima,
; en la séptima,
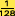 ; después
; después
 ;
;
 ;
;
 . ¿Podremos entonces escribir que
. ¿Podremos entonces escribir que 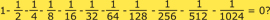
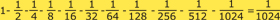
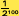 de metro, que es muy muy pequeño, pero no es cero. Y
podemos seguir sin parar porque siempre quedará un segmento de longitud
diferente de cero, ¡es infinitamente pequeño!
de metro, que es muy muy pequeño, pero no es cero. Y
podemos seguir sin parar porque siempre quedará un segmento de longitud
diferente de cero, ¡es infinitamente pequeño!