VI. APLICACIONES SELECTAS
LOS primeros capítulos de este libro se han dedicado a exponer y a discutir los conceptos más importantes de la termostática. Esto lo hemos llevado a cabo dentro de un marco de referencia histórico con objeto de presentar al lector, no sólo el concepto en sí, sino su evolución a través de diferentes épocas del pensamiento humano. Con ello no sólo hemos aclarado, sino enriquecido el contenido de las leyes de la termostática. Simultáneamente, esto nos ha llevado a minimizar el número de ejemplos específicos de sistemas macroscópicos que ilustran la versatilidad y la operatividad de estas leyes. A pesar de que el libro está enfocado fundamentalmente a la clarificación de los aspectos conceptuales de las leyes de la termostática, no queremos que el lector se quede con la impresión de que únicamente constituyen un bello y completo ejercicio del intelecto humano. O bien, que resumen un conjunto enorme de experiencias y que fuera de las aplicaciones obvias a la teoría y diseño de las máquinas térmicas, de la cual esencialmente se originaron, no tienen mayor relevancia. La situación es precisamente la opuesta. Es la única rama de la física que no se vio afectada por las dos grandes revoluciones científicas de principio de siglo, la teoría de la relatividad y la mecánica cuántica. Ello singulariza a la termostática y pone de relieve la universalidad de su contenido. Vale entonces la pena mostrar al estudioso de ella algunos de los múltiples sistemas donde es aplicable.
Por razones de espacio, y especialmente de uso de herramientas matemáticas sofisticadas, los ejemplos aquí vertidos se eligieron tratando de que las operaciones matemáticas involucradas no requieran más de los que una persona adquiere al nivel de sus estudios medios, secundaria y preparatoria. Al mismo tiempo se buscó una representatividad de las varias disciplinas en las cuales es de utilidad la termostática. Con ello invitamos al lector a consultar la extensa bibliografía que hay sobre la materia si desea profundizar en estos temas.
A) ALGUNAS APLICACIONES A LA INGENIERÍA
1) Consideremos una máquina térmica que opera en ciclos. Estos ciclos son
arbitrarios (no necesariamente reversibles) y la substancia operante es también
arbitraria. Esta máquina M, como se ilustra en la Figura 16, opera entre una
fuente de calor a una temperatura dada, digamos Tc y cede parte del
calor extraído de ella a otro cuerpo a menor temperatura Tf. En el
proceso, realiza una cierta cantidad de trabajo W que de acuerdo con la ecuación
(5), la primera ley de la termostática es igual a :
y recordamos que —W es la convención adoptada para el trabajo cuando
éste es realizado por el sistema sobre sus alrededores. Como la sustancia
operante, después de cada ciclo tiene un cambio neto en la entropía que es igual
a cero, Sf = Si, el único cambio de entropía es el que sufren los dos cuerpos
entre los cuales opera M que constituyen los alrededores.
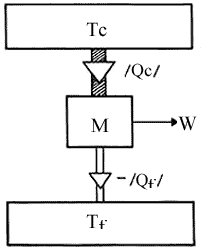
Figura 16. Una máquina térmica M operando entre dos cuerpos a temperaturas Tf Tc / y T/e, donde Tc > Tf.
De esta manera, (DS) sist. = 0
y por lo tanto
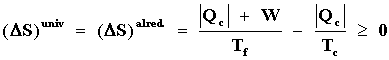
de acuerdo con la ecuación (15b) pues, por hipótesis,
los cuerpos no varían su temperatura (en el lenguaje habitual se consideran
como fuentes térmicas). Despejando -W de esta desigualdad, se obtiene que
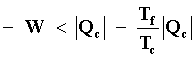
o sea que el trabajo máximo que podemos obtener de M, que ocurre cuando el
proceso cíclico por el cual se lleva la sustancia operante es ideal, es igual
a,
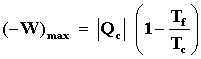
El lector ahora puede mirar la ecuación (9) y encontrar que justamente la eficiencia
máxima con que puede operar una máquina térmica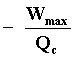 
,
ecuación (7), es igual a la de una máquina de Carnot operando entre los
dos cuerpos. Este pequeño cálculo da una demostración alternativa de este importantísimo
principio,11consecuencia
inmediata de la ecuación (15b)
2) Esta segunda aplicación ilustra de una manera clara y concisa
la connotación habitual que se hace de la entropía como una medida de la "energía
no disponible" para ser convertida en trabajo mecánico, v.gr., trabajo
útil cuando un proceso irreversible tiene lugar en la naturaleza.
Imaginemos a nuestro medio ambiente, un recinto a una temperatura media determinada,
o una bodega para almacenamiento de víveres, un frigorífico, o lo que sea. El
problema consiste en tomar un cuerpo de masa finita a una temperatura dada,
llamémosla T2, y enfriarlo a la temperatura de ese recinto que llamaremos
T0. Para ello usamos un refrigerador, esto es una máquina térmica
operando en ciclos que a expensas de un trabajo W suplido por una fuente externa
(un motor, etc.), extraiga calor del cuerpo dado y ceda otra cantidad de calor
al recinto, el cual por su extensión, funciona como una fuente térmica. (T0
no se altera.) (Fig. 17.)
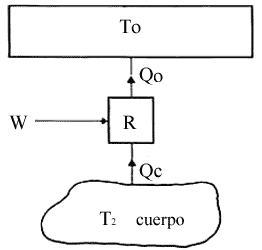
Figura 17. El refrigerador R calor |Qc| del cuerpo caliente y mediante el trabajo W lleva una cantidad de calor |Qo| al cuerpo frío To <T2.
En este caso, la primera ley expresada por la ecuación (5) establece que,
Como el cuerpo se enfría a la temperatura T0 su entropía cambiará
por una cantidad DSc que es igual a su
entropía a la temperatura final T0, llamémosla S0, menos
su entropía en el estado inicial a la temperatura T2, llamémosla
S2. El cambio en S en la sustancia operante en R es cero y el cambio
en T0 es
.
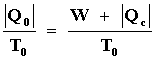De acuerdo entonces con la ecuación (15 b)
To (S2 - So ) - |Qc|
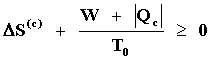
Por lo tanto, el valor mínimo posible de W, esto es, el refrigerador más económico
que obviamente es uno ideal (reversible) se logra si
lo cual permite estimar el costo de operación de una planta de refrigeración. Los valores de S2 y S0 se pueden consultar, para el refrigerante usado, en tablas donde los valores de S están tabulados como funciones de la temperatura.
Ahora combinemos las situaciones descritas en los dos anteriores e imaginemos
a una máquina térmica operando en ciclos entre una fuente térmica a una temperatura
T2 y la fuente más fría disponible (una tonelada de hielo, un tanque
de aire líquido, etc,). De acuerdo con el resultado del inciso 1) la máxima
cantidad de energía disponible como trabajo es igual a
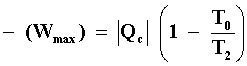
En este sentido, podemos afirmar que cualquiera energía contenida en la fuente térmica fría T0 y que pueda extraerse solamente en la forma de calor, no puede ser transformada en trabajo mecánico, esto es, no es una energía útil.
Imaginemos ahora un proceso irreversible simple como la conducción del calor,
descrito en la Fig. 15 donde el calor fluye por un conductor metálico entre
dos cuerpos a temperaturas diferentes, T2>T1. Llamemos
Q a la cantidad de calor que se ha transferido al cuerpo frío después de un
tiempo determinado. Si tomamos entonces al cuerpo frío a la temperatura T1
y ponemos a nuestra máquina a operar entre dicho cuerpo y la fuente a la temperatura
T0, el trabajo máximo que podemos obtener es:
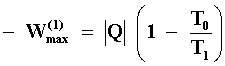
Pero si no hubiese tenido lugar la conducción de calor,
esto es el cuerpo a la temperatura T2 hubiese estado aislado del
cuerpo a T1, el trabajo máximo que M podría producir operando entre
T2 y T1 sería
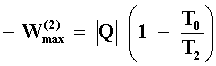
Esto es suponiendo que la máquina M extrae del cuerpo a T2 la misma
cantidad de calor que hubiera transferido al cuerpo frío por conducción. Si
restamos estas ecuaciones,
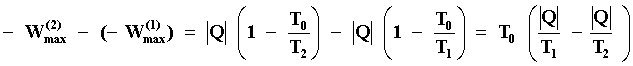
Como el único cambio de entropía en esos procesos es la del universo y ella
es precisamente igual al término entre paréntesis hemos obtenido un resultado
muy ilustrativo. El miembro izquierdo de la ecuación nos dice que si operamos
la máquina M entre la fuente fría T1 y la fuente auxiliar T0
después de que el proceso irreversible ha ocurrido, esto es, |Q| unidades de
calor se transfirieron del cuerpo caliente al frío, se obtiene una cantidad
de trabajo útil que es menor que la cantidad que se obtiene si la operación
de M es entre el cuerpo T2 y la fuente auxiliar T0 antes
de que el primero pierda por conducción el calor |Q|. Esto es, tal diferencia
es una medida de la energía que no está disponible para convertirse en
trabajo útil. Si la llamamos E, obtenemos que
|
E = T0 (DS)
univ.
|
(21) |
esto es, que la energía no disponible es el producto de la temperatura de la fuente térmica más fría que se tenga a la mano multiplicada por el cambio en la entropía del universo producida por el proceso irreversible, en este caso la conducción de calor. Aquí hemos demostrado este resultado haciendo uso de un proceso irreversible en particular pero puede hacerse, mediante un ejercicio más profundo de abstracción, de manera completamente general. La consecuencia primordial de esta ecuación es que cada vez que ocurre un proceso irreversible, se obtiene una cierta cantidad de energía que no es aprovechable como trabajo útil. Como los procesos irreversibles ocurren continuamente en la naturaleza, hay una cierta cantidad de energía derivada de ellos que no es convertible en trabajo útil. A este fenómeno, estudiado por primera vez por lord Kelvin se le conoce como el principio de la degradación de la energía. Nótese que aquí la ley de la conservación de la energía no se viola. Sólo se dice que al incrementarse la entropía, hay una cierta cantidad de energía que se transforma en otra forma, en la cual ya no es aprovechable. En términos más llanos diríamos que la energía "corre cuesta abajo".
B) ALGUNAS APLICACIONES A LA QUÍMICA
Las reacciones químicas constituyen uno de los capítulos más importantes de la físico-química contemporánea, no sólo por su naturaleza misma, sino porque tienen una cantidad enorme de aplicaciones que abarcan desde procesos industriales múltiples y variados hasta los complejos mecanismos de reproducción de las células vivas.
Una de las características más familiares de estos procesos es que su ocurrencia va acompañada siempre por una cantidad de energía conocida como "el calor de la reacción" . Hay una clase de reacciones químicas a las cuales hay que suministrarles energía para que puedan ocurrir y se les llama "endotérmicas". La otra clase es la que produce energía en forma de calor cuando tienen lugar y se les llama "exotérmicas", se llevan a cabo en recipientes que están a la temperatura ambiental y en contacto con la atmósfera, es usual referir esta energía (calor) liberada como cedida a la reacción a una temperatura de 25ñ C (298ñK) y 1 atm. de presión.
La fase en que participa la substancia en la reacción puede variar de manera
que si A participa en una reacción en fase gaseosa, se representa por A(g),
si lo hace en la fase líquida por A(1) y en fase sólida por A(s). De esta manera
en la formación del agua a partir de sus elementos, escribimos que
| H2 (g) + 
O2(g) ñ H2O(g) |
Q298 = -57.8  |
En esta reacción por cada dos átomos de hidrógeno en fase gaseosa que se combinan con un átomo de oxígeno, en fase gaseosa, se produce una molécula de agua en fase gaseosa. Además en la reacción, por cada mol de agua que se forma a 25ñC se liberan (Q es negativo si el sistema cede calor) 57.8 kilocalorías.
En el año de 1840, el químico alemán G. H. Hess enunció una regla empírica, conocida como la ley de Hess, la cual establece que el calor absorbido o cedido por una reacción química es el mismo, independientemente de que la reacción ocurra en uno o varios pasos.
Esta regla tiene, desde luego, la enorme ventaja de que es posible calcular
calores de reacción de reacciones químicas que no puedan estudiarse en el laboratorio.
Un ejemplo típico es la combustión incompleta del carbono sólido para formar
monóxido de carbono:
| C(S) + O2(g)
ñ CO(g) |
De acuerdo con la regla de Hess, podemos conocer el calor de esta reacción
a partir de otras por simple adición y substracción entre ellas. En este caso,
el calor de formación del bióxido de carbono es conocido,
| C(s) + O2(g) ñ
CO2 (g) |
Q298 = -94.052 |
y el calor de oxidación del monóxido de carbono, también es conocido,
O2(g) CO 2 ñ Q298
= —67.636
Si ahora reescribimos estas reacciones en la forma:
|
C(S) + O2(g) ñ
CO2(g) |
Q = -94.052 |
| CO2(g) ñ
CO(g) +
O2(g) |
y las tratamos como si fueran ecuaciones algebraicas, las fórmulas de los compuestos jugando el papel de variables algebraicas sumarlas obtenemos que
| C (s) +
O2 (g) ñCO (g) |
Nótese que en la segunda reacción que usamos, hicimos tácitamente la hipótesis de que es reversible y al invertirla le cambiamos el signo a Q. Si una reacción es exotérmica en una dirección opuesta y recíprocamente.
Vamos ahora a mostrar que la regla de Hess no es otra cosa que el resultado
de aplicar la ecuación (5), la expresión algebraica de la primera ley de la
termostática, a las reacciones químicas concebidas. como procesos reversibles.
Para ello comenzaremos por definir una nueva función termostática, la "entalpía"
de un sistema, que denotaremos por H. En efecto,
Nótese que, en virtud de que la energía interna U, así como la presión p y
el volumen V, son todas ellas variables o atributos medibles de un sistema también
lo es H. Esta función, como U, es una propiedad en un proceso ideal reversible,
entre dos estados de equilibrio de un sistema que ocurre manteniendo la presión
constante, esto es un proceso isobárico. Si llamamos D
la variación de la correspondiente función termodinámica entre ambos estados,
y de acuerdo con la ecuación (5), DU = DQrev + DWrev.
Pero en este proceso el único trabajo presente es debido a un cambio en el volumen, el cual como ya mostramos en el cap. V (ver fig. 6) es igual a — pDV, el signo menos debido a que una expansión ( D V positivo) implica trabajo realizado por el sistema contra los alrededores. Así pues, DU + pDV = DQrev y por lo tanto, igualando ambas expresiones,
| D
H = (DQrev )p |
(23) |
Esta ecuación indica que en cualquier proceso isobárico y reversible, el cambio en la entalpía es igual al calor transferido entre el sistema y sus alrededores. En este caso particular (DQrev)p no depende del proceso, por ser igual al cambio de la función H, que es una función inherente al estado de un sistema. Por ser las reacciones químicas procesos isobáricos concebidos idealmente como reversibles, la ecuación (23) es la expresión matemática de la regla de Hess. Esta ecuación (23) no es más que un combinación de la definición de H y del principio de conservación de la energía, o si se quiere, es la expresión de este principio para procesos isobáricos y reversibles.
La ecuación (23) es la razón por la cual en la mayoría de las obras sobre termodinámica química se encuentra que el calor de una reacción se expresa con el símbolo DH25ñC con la convención antes mencionada para el signo correspondiente. Veamos un par de ejemplos más.
1) El calor de formación de una substancia a partir de su calor de combustión, esto es la descomposición de una substancia en bióxido de carbono y agua es relativamente fácil de medir, pero es de mucho mayor utilidad conocer el calor de formación, esto es la energía necesaria para formar una sustancia a partir de sus elementos. Como ejemplo calculemos el calor del alcohol etílico C2H5OH a partir de su calor de combustión.
| C2H5OH (1) +
3O2(g) ñ 2CO2 (g) + 3H2O
(1) |
Además, sabemos que el calor de descomposición del agua es
| 3H2O (1) ñ
3H2(g) + 
O2 (g) |
DH 298
= 204.95 |
y el del CO2 es,
| 2CO2(G)ñ2C(GRAFITO)
+ 2O2(g) |
DH298
= 188.10 |
Si sumamos las tres reacciones algebraicamente, obtenemos que
| C2H5OH(1) ñ
3H2(g) + O2
(g) + 2C (grafito) |
DH298
= — 66.36 |
y si invertimos esta reacción,
| 3H2(g) +
O2 (g) + 2C (grafito) = C2H5OH(1) |
DH298
= + 66.36 |
lo cual implica que si queremos formar una mol de alcohol etílico a partir de sus elementos, tomando al carbono como grafito el estado más estable de este elemento tenemos que suministrar al sistema, hidrógeno, oxígeno y carbono, 66.36 kilocalorías de energía (en forma de calor).
2) El cálculo del calor de una reacción dada, a partir del calor de la reacción
de otras reacciones conocidas. De nuevo este procedimiento es muy utilizado
cuando la reacción en cuestión no es manejable o accesible en el laboratorio.
Por ejemplo, tomemos el calor de reacción de la hidrogenación de un hidrocarburo
olefínico como el eteno CH2 = CH2, para formar un hidrocarburo
saturado como el etano CH3 - CH3 de acuerdo con la reacción
|
C2H4 (g) + H2(g)
ñ C2H6 (g)
|
DH298
= ?
|
Como los calores de combustión de los correspondientes hidrocarburos así como
el calor de formación del agua son conocidos, usamos las reacciones respectivas:
| H2(g) +
O2 (g) ñ H2O (g) |
DH298
= -68.3 |
| DH298
= -337.3 |
| C2H6 (g) +
O2 (g) ñ2CO2(g) + 3H2O(1) |
DH298
= -372.8 |
Si ahora sumamos algebraicamente las dos primeras reacciones y al resultado
le restamos la tercera, obtenemos que la reacción química resultante es la reacción
buscada y su calor de reacción es
|
DH298
= -68.3 - 337.3 + 372.8 = -32.8
|
Vale la pena hacer notar que en el uso cotidiano de la termoquímica se hacen uso de tablas de calores de formación de muchas substancias, calculados bajo la convención de asignar el valor cero al calor de formación de cada elemento (H2, 02, C, etc.). El lector interesado en este tema puede consultar la vasta bibliografía al respecto.
C) LA TERMOSTÁTICA DE UN GAS IDEAL12
A lo largo de la exposición presentada en este texto hemos omitido totalmente
manipulaciones matemáticas de cualquier índole. Cierto, hemos recurrido al lenguaje
simbólico de las matemáticas para expresar ciertos resultados, pero con ellos
no hemos usado otras operaciones que las comprendidas en la aritmética elemental.
Sólo en el uso del símbolo 
hemos
recurrido al significado del concepto de integral como un proceso límite ejecutado
sobre áreas cada vez mas pequeñas. Pero no hemos pasado de ahí y lo hemos dejado
como tal, como un símbolo que representa una operación elemental bien definida.
Pero la física, para utilizarse en la solución de problemas concretos no sólo
recurre al lenguaje de las matemáticas para expresar conceptos a través de símbolos,
sino que, además, usa de las operaciones dictadas por la propia matemática para
llegar a resultados concretos. El propósito de esta sección es de llevar al
lector, cuyos conocimientos de matemáticas estén al nivel de lo que se espera
en un buen estudiante de preparatoria, esto es que sepa los rudimentos del cálculo
diferencial e integral, por un camino sobre el cual aprenda la forma de emplear
las leyes de la termostática.
Para ello hemos escogido a los sistemas ideales por ser los más simples de tratar a nivel operativo pero que, conceptualmente, ejemplifican sin restricción alguna los alcances y limitaciones de la termostática. Una vez que el lector más interesado por estas disciplinas capte la belleza y simplicidad de la teoría, seguramente se sentirá estimulado para proseguir con lecturas mas técnicas. Además tendrá la seguridad de que conceptualmente, el contenido físico de los problemas que estudie es similar, sino es que idéntico, al de los casos simples aquí presentados y que sólo difieren de ellos por las dificultades técnicas de las operaciones matemáticas involucradas.
Comencemos por definir el concepto de capacidad calorífica de una sustancia
o material dado. Si tomamos una masa conocida de dicho material y en un proceso
infinitesimal y reversible le suministramos una cantidad de calor 
para elevar su temperatura por una magnitud dT, al "cociente" /dT
se le conoce como capacidad calorífica de dicho material y se denota por la
letra C. Como además, por la primera ley de la termostática
= dU - 
,
ecuación (3)
 |
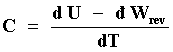La capacidad calorífica definida así es claramente dependiente del tipo de
proceso que se utilice para suministrar el calor. Si pensamos en un fluido o
un sólido de manera que, como ya mostramos con anterioridad,
(el signo es debido a la convención de que 
es negativo si el sistema realiza trabajo y eso ocurre en una expansión en la
cual dV > 0), la ecuación (24) se transforma en
 |
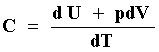Si durante el proceso de adición del calor, el volumen V se mantiene constante,
dV = 0, entonces la capacidad calorífica que se obtiene es aquella a volumen
constante Cv, donde
 |
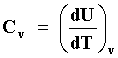El índice V fuera del paréntesis circular denota que el proceso ocurrió a volumen constante.
Por otra parte, si usamos un proceso a presión constante para ceder el calor,
y utilizamos la ecuación (22) notando que
si p = const., dp =0, obtendremos que la ecuación (25) se transforma en ese
caso en
 |
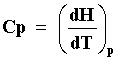Las ecuaciones (26) y (27) son dos de las fórmulas mas importantes de la termostática
pues Cv y Cp son cantidades relativamente fáciles de medir por métodos calorimétricos,
especialmente la segunda. Nótese que Cv y Cp no son independientes entre sí,
pues basta conocer una para determinar la otra. Imaginemos un gas para el cual
Cp es medible y además resulta ser sólo una función de la temperatura, Cp =
Cp(T). Entonces,
donde Ho es una constante. Conocida H, si conocemos también la ecuación
de estado de gas esto es pV = f(T,V) donde f (T,V) es una función conocida de
T y V, por la definición de H,
que por diferenciación respecto a T nos da el valor de Cv. Si el gas
es monatómico e ideal, 
donde R es la constante universal de los gases. Como f(T,V) = vRT
|
U = (
RT - RT ) v + H0 =
v RT + H0 |
esto es, la energía interna de un gas monatómico ideal es una función lineal
de la temperatura y Cv =
vR. Aquí, como antes, v denota el número de moles del gas en cuestión.
Véase entonces que
|
Cp - Cv = vR
|
una relación muy útil y bien conocida en la termostática clásica de un gas ideal. Es muy importante señalar que en estos cálculos simples la energía interna U y la entalpía H han quedado indeterminadas hasta una constante aditiva H0 cuyo valor no es obtenible de las leyes termostáticas mismas. Este hecho lo expresamos con todo cuidado desde la definición de U, ecuación (5), lo único que conocemos o podemos medir es DU.
Si ahora queremos conocer la entropía de un gas monoatómico usamos la definición
de Clausius, esto es, la ecuación (10) en forma diferencial, esto es, 
.
= dU +pdV
 |
(30)
|
Pero de la ecuación (28), dU = v
RdT y de la ecuación de estado, 
por lo tanto,
| (31) |
+ vR la cual por integración directa13
nos conduce al resultado
|
S(T,V) =
v
RlnT + vRlnV + S0 |
(32)
|
donde So es la suma de las dos constantes que aparecen cada una en las respectivas
integraciones logarítmicas. La ecuación (32) representa la entropía de v
moles de un gas monoatómico e ideal escrita como función de los dos grados
de libertad independientes, escogidos aquí para ser representados por las variables
T y V. Sin embargo de la ecuación de estado
y
que substituida en (32) conduce de inmediato a la expresión
| S(T,p) =
v RlnT - vRlnp + vRlnvR +  |
(33) |
que es ahora la forma de la entropía cuando se escogen T y p como variables independientes.
Invitamos ahora al lector a verificar que si de la ecuación (32) eliminamos
T en lugar de p, a través de la ecuación de estado, obtenemos que
| S(p,V) =
vRInp +
vRInV +
|
(34) |
donde
es una constante igual a
-
vRInvR.
Las ecuaciones, (32), (33) y (34) tienen múltiples aplicaciones, una de las cuales consideramos importante señalar aquí por su conexión con los ciclos, como el de Carnot, por los cuales se lleva a una sustancia operante en una máquina térmica.
Hemos repetido inumerables veces a lo largo del texto que es un proceso adiabático
si a lo largo de todo el proceso el calor transferido entre el sistema y los
alrededores es cero. En términos algebraicos, si el proceso es además reversible
=0 y por lo tanto dS =0, esto es la entropía es constante. Apliquemos esta restricción
a la ecuación (34) en la cual S(p,V) es por hipótesis constante, por lo tanto
S-
es también constante y hagamos uso de una simple operación algebraica llamando
a ésta constante lnB donde B es otra constante.14
vRInp
+
vRInV
y llamando 
elevamos
ambos miembros de la ecuación a la potencia 
obtenemos
finalmente que
Como en el caso del gas monatómico ideal, Cp =
vR, Cv =
vR
,que es un caso particular de otra ecuación más general,
|
pVg
= const
|
(35)
|
donde g es la relación entre las capacidades caloríficas y que es válida sólo cuando éstas son constantes. La ecuación (35) establece la llamada ecuación de las "adiabáticas" para un gas ideal (g =5/3 si el gas es monatómico) y determina la forma de la curva correspondiente en el plano p-V.
Como Cp > Cv siempre, g >1, en cualquier punto del plano pV una adiabática tiene una pendiente mayor que la isoterma que pase por dicho punto, pues para esta última pV=cte. Esto explica cualitativamente el porqué de la forma del ciclo de Carnot descrito en la fig. (5) si se piensa que la sustancia operante es un gas monatómico ideal.
El lector puede ahora verificar que si en lugar de haber comenzado con la ecuación
(34), lo hubiéramos hecho con las ecuaciones (32) o (33), los resultados serían
que pueden obtenerse también como casos particulares de las ecuaciones.
si de la ecuación (35) se eliminan p y V, respectivamente, usando la ecuación
de estado. (B1
B2)
El lector debe en este punto distinguir con toda claridad entre la ecuación
pV = vRT que representa una relación entre las tres variables
independientes p, V y T para cualquier gas ideal en estado de equilibrio
y la ecuación (35) o sus semejantes arriba escritas, que establecen la relación
entre dos variables independientes, cualesquiera que se escojan de la terna
p, V y T, cuando el gas sufre un proceso adiabático (
Q
=0) entre dos estados de equilibrio. O sea, estas ecuaciones definen los puntos
sobre la adiabática y no a cualquier punto del plano p-V que corresponde
a un estado de equilibrio.
Como un último resultado que pone de manifiesto el poder de la termostática,
volvamos a la ecuación (30) que ahora escribimos como
Para un gas ideal en general, dU = CvdT (de hecho se define un gas ideal
como aquel para el cual U es sólo una función de la temperatura T) donde, Cv
=
vR si el gas es monatómico, pero es una cantidad desconocida si no lo es.
Entonces,
Si dividimos cada miembro entre dT, y especificamos que el proceso de ceder
el calor (Q)rev
es a presión constante,
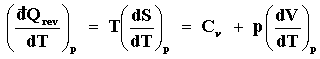
Pero por la ecuación (27), el miembro izquierdo es precisamente Cp luego,
 |
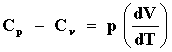(36) |
esto es, para un gas ideal la diferencia de calores específicos no es
arbitraria. Si examinamos el miembro derecho, nos damos cuenta además que su
conocimiento depende sólo de conocer la ecuación de estado que nos describe
cómo depende la presión p de T y V. En efecto, como en este caso pV = vRT
y 
especifica una variación en el volumen con la temperatura si p es constante,
despejando V de esta ecuación, V = vR/p T y derivando tenemos
= vR/p que substituido en la ecuación (36) reproduce la ecuación (29).
Ésta, como ya dijimos, es válida para cualquier gas ideal definido como aquel
para el cual U = CvT + cte y pV = vRT. Además, en este cálculo hemos aprendido
que de la expresión que antecede a la ecuación (36),
El lector puede verificar que si derivamos la ecuación (33 )con respecto a
la temperatura a presión constante, Cp = vR.
Este pequeño ejercicio muestra también el valor práctico de la función entropía.
Si conocemos su forma explícita como es el caso de la ecuación (33) para un
gas monoatómico ideal, como función de dos variables independientes, en este
caso p y T, por simple diferenciación se pueden obtener las capacidades caloríficas.
Veamos el otro caso:
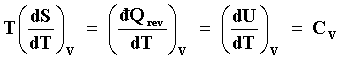
donde la serie de igualdades provienen de las ecuaciones (10), (25) y 26).
Si ahora diferenciamos la ecuación (32) a volumen constante, vemos que Cv
=
vR
Bien podría hacerse la pregunta ahora, y posiblemente el lector ansioso ya la tenga en mente, sobre el significado del resultado de tomar por ejemplo la derivada de la entropía respecto a la presión a temperatura constante, digamos en la ecuación (33). Veamos,
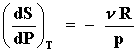
es una función de p. De nuevo, de acuerdo con la ecuación de estado el miembro
derecho no es otra cosa mas que — de
manera que obtenemos un resultado sorprendente,
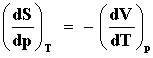
El cambio en la entropía respecto a la presión a temperatura constante es igual a menos el cambio en el volumen con la temperatura a presión constante, la entropía y el volumen, con signo menos, juegan un papel simétrico con respecto a cambios en la presión y la temperatura. De ahí que estas relaciones, descubiertas en el siglo XIX por J.C. Maxwell, se les llame de reciprocidad o relaciones de Maxwell. Desempeñan un papel crucial en la formulación y el uso de la termostática.
No es posible profundizar más a lo largo de estas líneas por estar dicho material fuera del contexto de esta obra, sin embargo deseamos que aquél que haya seguido estos argumentos hasta este punto, no titubee en consultar obras más extensas para penetrar en la materia. El camino difícil ya lo ha recorrido.
NOTAS
11 El lector debe comparar este ejemplo con la demostración ofrecida en el Apéndice A.
12 La lectura de esta subsección puede omitirse sin que se pierda la continuidad del texto.
13
In
º logaritmo natural, neperiano o de base e.
14 Es claro que si a es un número cualquiera siempre podemos encontrar otro número b tal que a = Inb=2.3 log10b sea que b = antilog 10 a/2.3
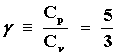