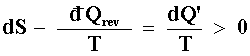V. PROCESOS IRREVERSIBLES. SISTEMAS ABIERTOS
EN TODA la discusión que hemos hecho en los capítulos anteriores para establecer el contenido de la segunda ley de la termostática y aclarar el concepto de entropía, nos hemos limitado a la consideración de sistemas cerrados (masa total constante) en ausencia de la acción de campos de fuerza externos, en particular, el campo gravitacional. También hemos hablado de la invalidez de la definición de entropía según la desigualdad marcada con la ecuación: (11) en sistemas que no cumplen con estas condiciones. Por otra parte, señalamos en el capítulo anterior que el concepto de entropía va asociado, en algunas interpretaciones, a una dirección en que ocurren los procesos naturales. Sin embargo, es necesario reconocer, aun en una obra tan elemental como ésta, que los problemas actuales de mayor interés en termostática son precisamente aquellos que involucran sistemas abiertos (biología, ingeniería, físico-química, cosmología, etc.), en presencia de campos externos (plasmas, cosmología, biofísica, etc.) y que por lo tanto merecen una atención especial. En conexión con el problema de la dirección de los procesos, su origen proviene del estudio de procesos irreversibles, los cuales son los que ocurren en la vida cotidiana, esto es, son los que percibimos en el mundo natural que nos rodea; no podemos olvidarnos de ellos. De aquí el título de este capítulo. Aunque conscientes del grado de dificultad involucrado en el estudio de estos problemas, intentaremos desglosar algunas de sus facetas más interesantes evitando el uso de un pesado arsenal matemático.
Comencemos primero por hablar de los sistemas abiertos, que brevemente tocamos en el capítulo anterior. Su importancia fue reconocida hace más de cien años por el gran físico norteamericano J. W. Gibbs. En su monumental obra sobre varios tópicos de matemáticas, física y fisico-química se encuentra un capítulo, que de hecho es todo un texto, sobre un trabajo desarrollado esencialmente entre los años de l875 y 1878 intitulado "Sobre el equilibrio de sustancias heterogéneas". En él Gibbs estudia no sólo los efectos químicos, esto es, provenientes de intercambios de masa entre sistemas en equilibrio, sino también los efectos que sobre el equilibrio tienen fenómenos tan complicados como la fuerza de la gravedad, la capilaridad y los esfuerzos tensiles inhomogéneos. La complejidad matemática involucrada en este tratamiento lo pone fuera de los alcances de esta obra, pero es conveniente y necesario hablar aquí sobre las implicaciones del trabajo de Gibbs en función de los resultados que hemos obtenido, tanto para la formulación matemática de la segunda ley, la ecuación (11), como para el significado de la función entropía, ampliamente discutido en el capítulo anterior.
Un sistema heterogéneo según Gibbs, es el formado por una colección de sistemas homogéneos que están separados entre sí por paredes, superficies u otros medios que permiten el paso de materia de un sistema homogéneo a otro. Cada sistema homogéneo, o fase como los llamó Gibbs, está constituido por una o varias sustancias constituyentes cuyas propiedades termostáticas, presión, temperatura, densidad, etc. son las mismas en cada uno y todos los puntos del sistema, de ahí la calificación de homogeneidad. Un ejemplo ilustra mejor estas ideas. Imaginemos que en un matraz cerrado herméticamente por su boca (Fig. 12) colocamos sal de cocina (cloruro de sodio) en agua de manera que no toda la sal se disuelva en ella, esto es, a modo de obtener una solución de cloruro de sodio, y dejar un remanente sólido en el fondo del matraz. Si tenemos el matraz digamos a 40º C, en la parte superior de solución existirá un poco de agua como vapor. Así obtenemos un sistema heterogéneo formado por tres fases, una fase sólida homogénea formada por la sal no disuelta, otra fase líquida homogénea formada por la solución de la sal en agua y otra formada por el vapor de agua. La separación entre las fases está proporcionada en este caso por dos interfases, la superficie líquida que separa al vapor de la solución y las superficies de los cristales de cloruro de sodio que separan al sólido de la solución. Claramente hay un intercambio de materia entre las fases pues el agua de la fase vapor se puede condensar sobre el líquido al mismo tiempo que el agua del líquido se evapora y las moléculas de la sal en la solución pueden pasar a la fase sólida en tanto que otras de ésta pueden pasar a la fase líquida.
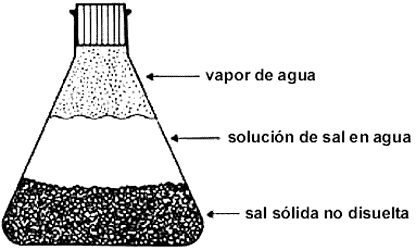
Figura 12. Ejemplo de un sistema heterogéneo formado por sal,
solución de sal en agua
y vapor de agua.
Como la solubilidad de una sal en el agua es función de la temperatura, así como lo es también la rapidez de evaporación de un líquido, podemos variar las proporciones de sal que hay en las fases sólida y líquida, y de agua en las fases líquida y vapor, calentando o enfriando el contenido del matraz.
Pero a una temperatura constante el contenido de sustancias en cada fase permanece constante. Esto no implica que cese la evaporación del agua o la disolución de la sal, lo que implica es que la rapidez con que el agua se evapora es la misma con que se condensa y que, análogamente, la rapidez con que se disuelve la sal es igual a la rapidez con que cristaliza. La función que exhibe este comportamiento a un nivel macroscópico se conoce como el "potencial químico". Como en este ejemplo una fase, la líquida, tiene dos componentes, agua y sal, para que exista el equilibrio termostático es necesario que:
1) El potencial químico del agua en la fase vapor sea igual al del agua en la fase líquida.
2) El potencial químico de la sal en la fase líquida sea igual al potencial químico de la sal en la fase sólida.
Estos enunciados (1) y (2) constituyen la expresión matemática de las igualdades entre las velocidades con que deben ocurrir los procesos arriba señalados. En una forma completamente general, para un sistema formado por F fases en las cuales existe un número arbitrario C de substancias componentes, el resultado de que en equilibrio todos los potenciales químicos de la misma substancia en cada una de las fases, deben ser iguales entre sí es uno de los más grandes logros del trabajo de Gibbs. De hecho, de aquí surge uno de los resultados más ricos de toda la termostática clásica conocido como la famosa regla de las fases de Gibbs. Veamos su deducción para el sistema descrito en la Fig. 12. Aparte de las concentraciones de agua y sal en cada una de las fases, que suman cuatro, dos del agua y dos para la sal, el sistema tiene 2 grados de restricción adicionales, una térmica (T=const) y otra geométrica (V=Cte). Luego hay seis grados de restricción en total. Las seis variables independientes las tomaremos aquí como las cuatro concentraciones, T y p, la presión.
Si queremos determinar unívocamente el estado de equilibrio, según un
teorema bien conocido del álgebra, necesitamos seis ecuaciones que relacionen
estas variables entre sí. Veamos cuantas tenemos: hay dos expresadas por las
igualdades entre potenciales químicos [enunciados (1) y (2)] y dos más que provienen
de la conservación de la masa, la masa total del agua y de la sal dentro
del matraz son constantes. Sólo tenemos cuatro ecuaciones que relacionen estas
variables, dos que provienen de las dos componentes y que expresan la conservación
de la masa y dos que expresan la condición de equilibrio. Si definimos al exceso
en el número de variables sobre el número de ecuaciones como el grado de variación
y lo llamamos f, vemos que en este caso
Esto es, en este sistema tenemos a nuestra disposición 2 de los 6 grados de
libertad que corresponden a las 6 restricciones inherentes al sistema, para
determinar sus estados de equilibrio. El sistema de la Fig. 12 es entonces un
sistema bivariante. En un sistema formado por F fases con C constituyentes
en ellas hay obviamente C(F-l) ecuaciones del tipo (1) y (2), F ecuaciones de
conservación de la masa y CF+2 variables si el sistema, como el del ejemplo,
está contenido dentro de un recipiente cerrado a temperatura constante. Entonces,
| (19) |
que es la famosa regla de las fases de Gibbs: el número de grados de variación en un sistema heterogéneo con F fases y C constituyentes, es igual al número de constituyentes menos el número de fases más dos.
El ejemplo más conocido de la ecuación (19) es el punto triple de una sustancia pura (C=1) definido como aquel donde coexisten simultáneamente las tres fases sólida, líquida y gaseosa (F=3). En este caso f=O, esto es el punto es uno invariante; el equilibrio está determinado por un solo valor de la presión y de la temperatura. Para el agua este punto ocurre a una temperatura de 273.16ºK y una presión de 4.58 mm de mercurio.
Sin embargo donde la ecuación (19) encuentra un campo fecundo de aplicaciones es en toda la teoría de soluciones multicomponentes pues permite determinar el número de variables independientes f, disponibles para determinar los estados de equilibrio. Los correspondientes diagramas que se obtienen son los llamados diagramas de fase.
Cuando las soluciones son sólidas, en particular entre metales, se utilizan para determinar las temperaturas y composiciones a las que existe el equilibrio entre las diferentes fases. Esto, como el lector puede inferir, tiene una importancia enorme en la metalurgia. Veamos un ejemplo muy simple: el plomo Pb y el antimonio Sb son miscibles en todas proporciones en la fase fundida, líquida. En la fase sólida cristalizan y son insolubles. El punto de fusión del Sb es de 630º C y el del Pb es de 326º C. En la Fig. 13 el punto A es el punto de fusión del antimonio y B es del plomo. La curva AE representa aquellos estados en que coexisten en equilibrio la solución sólida de Sb y Pb, el Pb sólido y la fase vapor. Como F=3 y C=2, f=l, sólo hay una variable independiente; esto es el equilibrio entre estas fases sólo puede ocurrir a las temperaturas y composiciones correspondientes a los puntos sobre AE.
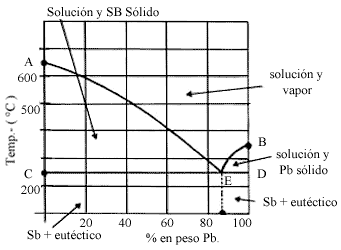
Figura 13. Diagrama de fase para el eutéctico de antimonio y
plomo.
Lo mismo, la curva BE representa las temperaturas y composiciones a las cuales las tres fases, vapor, solución y Pb sólido coexisten en equilibrio. Pero en el punto E hay cuatro fases presentes, la solución, el vapor, el Sb sólido y el Pb sólido, luego f=O. El punto E se conoce como el punto eutéctico y la mezcla como mezcla eutéctica, formada en este caso por 87% de Pb y 13% de Sb a 246º C. Este punto desempeña un papel similar al del punto triple en el caso de una sustancia pura, para soluciones sólidas sólo hay uno. La región bajo las curvas AEC, es aquella donde el Sb sólido y la solución pueden coexistir en equilibrio en tanto que la solución y el Pb sólido pueden coexistir en los puntos dentro de la región EBD.
El diagrama de fases entre el hierro y el carbono, que es mucho más complicado que el anterior por la formación de algunos compuestos entre ambos elementos, es de vital importancia en la fabricación de aceros pues las diferentes regiones de coexistencia corresponden a los varios tipos y calidades de los aceros.
Pero volvamos al tema de la validez e interpretación de la segunda ley de la termostática en particular de la ecuación (11) en el caso de los sistemas abiertos. Consideremos el ejemplo ilustrado en la Fig. 12 donde la temperatura se mantiene constante permitiendo que el contacto con un cuerpo (baño de agua, trozo de hielo, etc.) a la temperatura deseada. Si ahora identificamos al universo termodinámico como el cuerpo y el matraz, este último concebido como un solo sistema sin importar su contenido, en tanto que esté en equilibrio, podemos hacer uso de la interpretación dada en la ecuación (15a) para establecer el cambio de entropía en el universo en un proceso reversible, o por la ecuación (15b) si es irreversible. Desde este punto de vista no hay problema alguno. Las dificultades aparecen cuando intentamos calcular el término (DS)sist y reconocemos que el sistema está formado por una colección de fases, esto es, que tenemos un sistema heterogéneo. Si ahora queremos calcular el cambio en la entropía de cada fase durante el proceso, es necesario establecer la forma en que depende de las variables independientes y esta dependencia no está contenida en la formulación anterior de la segunda ley. Pero como hicimos notar en discusiones anteriores, tampoco sabemos calcular la energía interna de cada fase pues la definición dada en la ecuación (1) sólo es válida para sistemas cerrados. Entonces, aunque partamos de la hipótesis de que sepamos cual es la energía de cada fase, aislada del resto, en el momento de ponerlas en contacto entre sí no sabemos, a priori, si sus valores van a cambiar o no. Como ya también hicimos notar, la solución a esta cuestión requiere de una hipótesis adicional no requerida hasta ahora. Dicha hipótesis es que todas las variables extensivas en un sistema heterogéneo son aditivas, esto es, la energía interna es la suma de las energías de cada fase, la entropía total es la suma de las entropías, etc.
Bajo estas condiciones, entonces, el cálculo de (DS)sist . es muy simple, se reduce a sumar las contribuciones de para cada fase. Pero insistimos una vez más, el cambio en la entropía de cada fase como un sistema independiente no satisface una desigualdad de la forma exhibida por las ecuaciones (11) o (15a) si el proceso es reversible. Estas son aplicables, exclusivamente a un sistema o un universo termodinámico cerrado en el primer caso, cerrado y aislado en el segundo, independientemente de que como parte de dicho universo existan sistemas abiertos. Es posible que una concepción de esta índole haya estado en la mente de Clausius cuando dijo que la entropía del universo tiende a un máximo. Si así es y el universo es el cosmológico, tendrá que ser concebido a fortiori como cerrado y aislado.
Para ejemplificar estos razonamientos volvamos al sistema de la Fig. 12. Si
concebimos al matraz con su contenido y al baño que lo rodea como el universo,
para todo proceso reversible
(DS) sist. = (DS) sal + (DS) solución + (DS) vapor
donde el signo ± en el segundo renglón depende de si el baño recibe o cede
una cantidad de calor DQrev.
Cómo (DS) univ. = O,
por ser el proceso reversible.
Pero el signo particular de cada una de las contribuciones a (DS)sist. dependerá de la naturaleza específica del proceso que se lleva a cabo. Y por último, insistimos en que en esta prescripción para calcular (DS)sist. se están ignorando las posibles contribuciones de las interfases, las cuales, como hicimos notar en el capítulo anterior, no son siempre a priori despreciables. Es así como en la termodinámica de sistemas abiertos se han resuelto, hasta ahora, los problemas conceptuales derivados de la extensión de las leyes de la termostática al dominio de ellos.
Pasemos ahora a considerar el caso de los procesos irreversibles. Si un proceso irreversible tiene lugar en un sistema cerrado y aislado su entropía forzosamente aumenta. Este es el caso de la remoción de una restricción y por lo tanto del correspondiente proceso inducido. Si el sistema no es aislado pero es cerrado, y si todavía suponemos que la acción de un campo externo es nula o despreciable, entonces la entropía del universo es la que debe ser positiva. Este resultado está expresado por la ecuación (15b). Insistimos en recordar al lector que esta ecuación contiene dos términos, uno que proviene del cambio de la entropía del sistema y otro del cambio de entropía del cuerpo con quien está en contacto. Entonces, la variación de la entropía de una, por ejemplo, del cuerpo, puede disminuir, a expensas de que la variación de la entropía del cuerpo aumente, y este aumento debe ser de tal magnitud que la suma sea mayor que cero. Un ejemplo muy simple ayuda a comprender este efecto. Imagine el lector un gas encerrado en un cilindro con paredes metálicas dotado de un pistón. El cilindro está en contacto con la atmósfera del recinto donde está ubicado y en equilibrio térmico con ella. Supongamos que inicialmente el gas se encuentra comprimido a una presión mucho mayor que la atmosférica, digamos 10 atm. Si soltamos el pistón el gas se expande bruscamente (¡proceso irreversible!) hasta alcanzar el equilibrio con la presión atmosférica. En este caso, si la temperatura se mantiene constante, el gas debe ceder una cierta cantidad de calor Q a la atmósfera, la cual consecuentemente, varía su entropía por Q/T. La suma de Q/T y la variación de la entropía del gas tiene que ser positiva. Así pues, para sistemas cerrados y aislados, la ecuación (15b) puede interpretarse fácilmente.
Para un cambio infinitesimal y reversible,
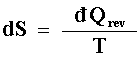
Si el cambio no es reversible,
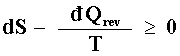
que de hecho no es más que una forma conveniente escribir la ecuación (11),
la igualdad cumpliéndose para procesos reversibles. De esta fórmula tan simple
ha surgido toda la inquietud y, subsecuentemente, la termodinámica de procesos
irreversibles. En efecto, salta, a la vista una pregunta inmediata ¿Cómo podemos
escribir la diferencia entre estos dos términos cuando un proceso es irreversible?
El lector que haya pensado esencialmente en una contribución que provenga de
la fricción, habrá acertado. En efecto en 1850 Clausius mismo propuso que esta
diferencia fuese igual a un término que él llamó el "calor no compensado" y
que llamó d Q'. Entonces,
| (20) |
Sin embargo, nunca dio una descripción más precisa del término fuera de asociarlo con una medida del grado de irreversibilidad de un proceso. Fue W. Thomson, lord Kelvin, quien en 1854 se dio cuenta por primera vez de efectos irreversibles en sistemas termodinámicos y obtuvo resultados concretos a partir de una fórmula de la naturaleza de la ecuación (20).
Esto ocurrió cuando se puso a estudiar dos efectos de la termoelectricidad descubiertos, uno en 1821 por el físico alemán T. J Seebeck y el otro por el relojero francés J.C.A. Peltier, en 1836. Dada la simplicidad de esos fenómenos y su relevancia en conexión con el esclarecimiento de la ecuación (20) vamos a estudiarlos con cierto detalle.
Consideremos un termopar que consiste de dos alambres conductores diferentes
que llamaremos A y B, respectivamente, y cuyas juntas están en contacto con
dos cuerpos que se encuentran a temperaturas diferentes T y Tr, siendo
Tr la temperatura de la junta que se toma como referencia. (Fig.
14). Supongamos ahora que Tr se mantiene constante, en tanto que
la temperatura del cuerpo T se hace variar (T ¹ T,)
y los extremos b y b' del conductor B se conectan al voltímetro como se ilustra
en la figura.
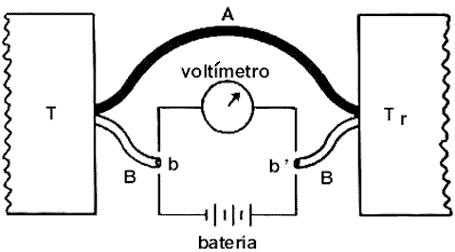
Figura 14. Termopar AB con juntas en los cuerpos a temperaturas
T y Tr.
Lo que se observa es que el voltímetro registra una lectura que corresponde a una fuerza electromotriz EAB generada en el circuito cuyo valor depende de T. A este efecto se le conoce como el efecto Seebeck y a la razón de cambio de EAB se le conoce como la fuerza o potencia termoeléctrica del termopar.
Ahora supongamos que en el dispositivo ilustrado en la figura, hacemos las dos temperaturas T y Tr iguales y conectamos los extremos b y b' con a una batería que genera una cierta corriente i a través del circuito. Lo que se observa es que en las juntas de los termopares la temperatura aumenta por una cantidad que excede en valor al calentamiento provocado por el calor de Joule y que es igual a i2 R donde R es la resistencia eléctrica del circuito. Recuerde el lector que este calor es generado precisamente por la fricción interna en el circuito, esto es, la resistencia que opone el conductor al paso de la corriente. El cambio en la temperatura no acreditable al efecto Joule como el efecto Peltier.
La cantidad que puede medirse experimentalmente, es la rapidez con la cual se produce este calor, cantidad que resulta proporcional a la corriente i (¡no a i2 !).
Al coeficiente de proporcionalidad se le conoce como el coeficiente de Peltier.
En su estudio de este problema donde aparecen dos efectos irreversibles,
la conducción de calor por los conductores y el calor de Joule, lord Kelvin
supuso que éstos podían ignorarse sobre las bases de que son aparentemente independientes
de los efectos de Peltier y el efecto Thomson. Más aún, este último es el efecto
Seebeck excepto por que lo que se observa es la distribución de temperatura
a lo largo de los alambres cuando no circula corriente eléctrica, que son efectos
reversibles. Bajo esta hipótesis y sumando todos los cambios de entropía, suma
que es cero para procesos reversibles, obtuvo fórmulas explícitas para los coeficientes
de Peltier y de Thomson que han sido ampliamente verificadas experimentalmente
y por lo tanto consideradas como correctas. Sin embargo esos efectos, Seebeck,
Peltier y Thomson están indudablemente conectados de una manera obviamente intrincada
con los efectos irreversibles y por lo tanto con el calor dQ' introducido por
Clausius. La forma en que esta conexión ocurre está muy lejos de los alcances
de este texto y fue dada por el gran químico noruego Lars Onsager en 1931, trabajo
que le valió el premio Nobel de química en 1968. Sin embargo la idea medular
es un tanto simple de explicar. Veamos primero la idea en un sistema cerrado
pero en contacto térmico con un medio ambiente a una temperatura T. Entonces,
la entropía total S puede variar por dos posibles mecanismos, uno es el intercambio
de calor con sus alrededores, el medio ambiente, a la temperatura T. Este cambio
es externo y lo designamos por (dS)e. Pero, por otra parte, dentro
del sistema pueden generarse fenómenos irreversibles provenientes precisamente
de "la fricción" inherente a los procesos mismos que generan un cambio en la
entropía. Este cambio usualmente denominado "producción de entropía" lo llamamos
(dS)i. Entonces, dS =(dS)e + (dS)i pero como
además ![]() ,
,
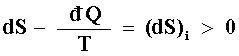
de acuerdo con la interpretación habitual de la ecuación (20). El calor no compensado de Clausius es ahora substituido específicamente por la producción de entropía, asociada a los mecanismos de fricción internos, inherentes al sistema mismo.
Si el sistema es abierto, por sus fronteras puede fluir no sólo calor, sino materia la cual, a su vez, puede ser portadora de una cierta cantidad de entropía que proviene de efectos como el de difusión, conducción de calor, etc., y en ese caso (dS)e ya no tiene una expresión tan simple como en el caso anterior. El gran mérito de Onsager es haber proporcionado una teoría que permite deducir las ecuaciones diferenciales (usualmente no lineales) que gobiernan estos fenómenos y cuya solución es en principio posible bajo condiciones preestablecidas.
Llegamos a nuestra pregunta final de este capítulo, a saber, ¿qué conexión hay entre la ecuación (20) y la flecha o dirección en los procesos irreversibles? El lector muy cauteloso ya se habrá percatado de lo general y complejo de esta pregunta. Es muy posible que por su mente se cruce una respuesta que es inmediata y además correcta: si en un sistema cerrado y aislado removemos una restricción, inducimos un proceso que ocurre siempre en la dirección en que la entropía aumenta.
Así pues, para estos sistemas, la dirección de un proceso inducido (mal llamado espontáneo) está bien determinada. Pero si el proceso ocurre en un sistema cerrado pero no aislado o abierto la respuesta ya no es tan inmediata y de hecho no involucra a la entropía.
Por ejemplo, si tomamos un sistema en el cual en lugar de conservarlo aislado, mantenemos la presión y la temperatura constantes, en cuyo caso, como insistimos en el capitulo anterior, el sistema no puede permanecer aislado por ser ambas variables intensivas. Entonces ya no es la entropía la función cuyo cambio dicta o determina la dirección del proceso, sino otra función. Y es más, dependiendo de qué variables (restricciones) mantengamos fijas en el proceso, serán diferentes las funciones que determinen la dirección en que el proceso inducido ocurra. Esta colección de funciones, una para cada proceso diferente de acuerdo con las restricciones impuestas, se conocen como potenciales termodinámicos. La entropía es un potencial termodinámico sólo para aquellos procesos inducidos que tienen lugar en sistemas aislados y cerrados. Es pues un error grave el tratar de singularizarla como función privilegiada y de darle u otorgarle un criterio de universalidad como una directriz de un cambio. De aquí la respuesta a la primera parte de la pregunta: sólo en sistemas aislados y cerrados el cambio en la entropía constituye un criterio para decidir si un proceso inducido es o no factible.
La segunda parte de la pregunta es mucho más complicada de responder y en opinión del autor corresponde más a un buen deseo que a un hecho bien establecido. Esta parte concierne con asociar en alguna forma una dirección en el tiempo a la entropía como una medida de la irreversibilidad. Es cierto que los procesos irreversibles, en especial aquellos asociados con el concepto de "envejecimiento" van inevitablemente acompañados de una evolución en el tiempo que siempre apunta hacia el futuro y nunca hacia el pasado. Esta dirección en el tiempo se refleja de muchas maneras en el sistema que estamos observando, dependiendo de su complejidad.
Si se analiza un proceso irreversible simple como el flujo de calor en un conductor
metálico rígido cuyos extremos están en contacto con dos cuerpos a temperaturas
diferentes, una mayor que la otra, la irreversibilidad en el flujo de calor
se manifiesta en que podemos escribir una ecuación que nos dice cómo varía la
temperatura en cada punto, digamos x, del conductor a cada tiempo t. (Ver Fig.
15.) Esta ecuación tiene una estructura tal que si cambiamos t por -t no
permanece igual, esto es, no es invariante frente a esta transformación. Si
el contacto se establece entre el metal y los cuerpos a un cierto instante,
llamémosle t=0 entonces, el flujo de calor que observamos a todo t>0, es
siempre en la dirección de T2 a T1. El flujo de calor
es un efecto irreversible y sólo se observa para tiempos mayores que cero. Por
lo que hemos visto con la ecuación (20) esto corresponde a una producción de
entropía (dS)i >O. ¿Puede este argumento extenderse con toda libertad
a cualquier sistema en el que ocurran procesos de nacimiento, vida y muerte,
como los seres vivos, las galaxias, el universo, etc.? Varios autores muy distinguidos
como Schroedinger, Von Bertalanffy y más recientemente Prigogine, Haken, Eigen
y otros han hecho esfuerzos en esta dirección y los resultados obtenidos por
ellos son muy discutibles. La pregunta misma sobre si las leyes es de la termostática
y la termodinámica de procesos irreversibles son aplicables en su forma convencional
a estos sistemas, no está claramente establecida. Ni en el caso de sistemas
biológicos donde no estamos tratando con materia inerte, ni en el caso cosmológico
donde el efecto de los campos externos y la curvatura del espacio no son despreciables.
El problema es en sí muy atractivo, pero existe un consenso bastante diseminado
entre los físicos de hoy en día expresando dudas serias acerca de su posible
descripción con ideas tan primitivas. Así, la respuesta a esta segunda parte
de la pregunta todavía no está bien comprendida.
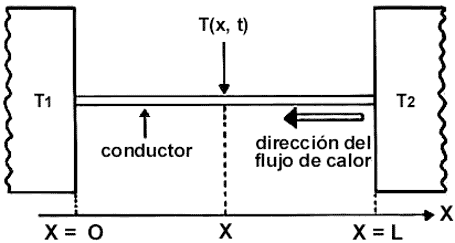
Figura 15. Conductor metálico rígido de longitud L colocado entre dos cuerpos
a diferentes temperaturas, T2 > T1