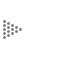VII. DIAGRAMA DE ESTADO DE UNA SUBSTANCIA REAL

PARA una sustancia pura, con una masa constante digamos 1 mol(v = 1) encerrada en un recipiente cuyo volumen es V y su temperatura T, se tienen dos restricciones. Consecuentemente, se requieren dos variables independientes para describir sus estados de equilibrio que usualmente se escogen, por razones estrictamente de conveniencia experimental, de entre la terna p, V y T. Pero que sólo dos sean independientes implica que si se fijan sus valores, el de la tercera queda automáticamente determinado y eso, matemáticamente, se expresa diciendo que hay una relación funcional entre estas variables de manera que

p = f (V,T)

Aquí f es símbolo que denota una operación que genera un valor de p conocidos los valores de V y T. En el caso de un gas ideal la operación es muy simple pues p = R y f es la división de T entre V multiplicada por la constante R (para 1 mol de gas). A estas relaciones entre las variablesV y T se les conoce como "ecuaciones de estado". En un espacio euclidiano de tres dimensiones caracterizado por tres ejes mutuamente perpendiculares entre sí, al graficar los valores de p, V y T se obtiene una superficie muy complicada, que se conoce como superficie p-V-T y que por consiguiente, es muy difícil de analizar. Cuando se proyecta esta superficie sobre los planos p-V y p-T, los dos más utilizados en la práctica, se obtienen en primer caso un conjunto de curvas T=T(p,V) que para cada valor de T representan las isotermas del fluido del que se trata. En el segundo caso, se obtienen las curvas a lo largo de las cuales el volumen V es constante. Ambos diagramas que, repetimos, se construyen a partir de mediciones experimentales de las variables p, V y T, contienen toda la información que uno desea sobre dicha sustancia, información que es mucho más fácil y eficiente de asimilar al amparo del contenido físico de las leyes de la termostática. Nuestra intención es ilustrar aquí algunos fragmentos, los más importantes, de un análisis de este tipo.

Empecemos con un ejemplo trivial, el del gas ideal. Como ya hemos indicado con anterioridad en el plano p-V, las isotermas (T = cte) son curvas que satisfacen la ecuación pV=const, esto es, son hipérbolas equiláteras como se muestra en la Fig. 16a. En el plano p-T las curvas V=cte. (curvas isométricas) satisfacen la ecuación p = T= const. T, i.e, son rectas convergentes en el origen cuya pendiente depende del valor de la constante . A medida que V aumenta, la pendiente disminuye (Fig. 16b)

Figura 16a. Isotermas para un gas ideal.

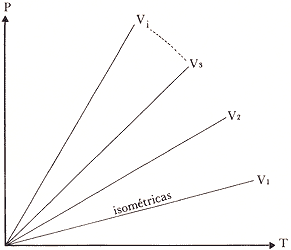
Figura 16b. Isométricas para un gas ideal V₁ > V₂ > V₃, etc.

Para una sustancia pura, la situación es completamente diferente. Históricamente, fue el físico escocés T. Andrews quien en 1869, por vez primera, reportó los datos p-V-T obtenidos a partir de la experimentación llevada a cabo con un gas real. La sustancia empleada por Andrews fue el CO₂ que tiene una densidad de 1.977 g/l en la fase gaseosa a 20ñC, de 1.101 g/l en la fase líquida a -37ñC y de 1.56 g/l a 79ñC, en la fase sólida. El CO₂ tiene también un punto de fusión -56.6ñC y una presión de 5.2 atmósferas en tanto que el líquido hierve a -78.5ñC en el punto de sublimación. Andrews en sus experimentos tomó una masa conocida de este gas y en un tubo de ensaye, herméticamente cerrado y mantenido a una temperatura fija, midió los volúmenes que ocupa el gas a presiones diferentes. Graficando los resultados en un diagrama p-V, obtuvo los resultados que se muestran en la Fig. 17.

La temperatura más baja empleada por Andrews fue de 13.1ñC. A bajas presiones observó que el C0₂ es gaseoso; hasta el punto en que la presión alcanza el valor de aproximadamente 50 atmósferas el volumen disminuye en la porción de la curva AB más o menos de acuerdo con la ley de Boyle. En el punto B comienza la licuefacción y el volúmen disminuye hasta convertirse en líquido a presión constante. Esta licuefación está representada por la porción BC de la curva en la Fig. 17. En C, todo el bióxido de carbono es líquido y la pendiente tan pronunciada exhibida por la porción CD, es sólo muestra de la mayor dificultad que existe para comprimir el líquido. La fase sólida sólo se obtiene a presiones muy altas y no es representable en éste diagrama.

Si repetimos este proceso incrementando la temperatura, el esquema se repite como lo muestra la isoterma a 29.93ñC en la Fig. 17 excepto porque la parte horizontal que describe la etapa en que ocurre la licuefacción, es más corta. Esto es común a todas las isotermas hasta llegar a la que corresponde a la temperatura de 31.1ñC en la cual esta porción horizontal se reduce a un solo punto. A temperaturas mayores de 31.1 ñC Andrews encontró que el CO₂ no puede licuarse aún sometiéndolo a presiones de algunos cientos de atmósferas, esto es, sigue comportándose como un gas que no puede licuarse.

Así pues el diagrama p-V para este fluido tiene toda una región a la derecha y arriba de la porción BPc de la curva punteada de la Fig. 17 en la cual se comporta como un gas. A la izquierda de la curva CPc es un líquido, y en todos los puntos dentro de la curva BPcC el gas coexiste en equilibrio con el líquido, razón por la cual se llama la región heterogénea. La curva BPcC que separa a las dos regiones que representan a las fases gaseosa y líquida, respectivamente recibe el nombre curva de coexistencia y consta de la envolvente gaseosa BPc y la envolvente liquida CPc. Ambas se unen en el punto Pc que tiene la propiedad de señalar los valores de la temperatura y la presión arriba de los cuales cesa la coexistencia entre las dos fases.

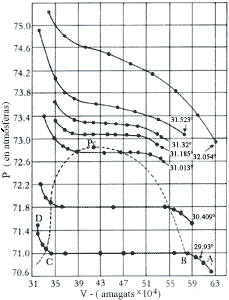
Figura 17. Isotermas del CO₂ en grados centígrados. ( 1 amagat = volumen ocupado por el gas a 0ñC y 1 atm. de presión) C es el punto crítico del fluido. Los puntos A, B, C y D están indicados sobre la isoterma a 29.93ñC. J. Michels et al. Proc. Roy. Soc. (Londres) A 160, 367, (1937)

A este punto se le conoce como el punto critico.

En el caso del C0₂ los valores de Tc y P_c que definen a dicho punto son de 31.1ñC y de 73 atm. respectivamente, llamadas la temperatura y presión críticas respectivamente. La isoterma a 31.1ñ es la isoterma crítica. Arriba del punto crítico solo existe una sola fase, situación que para muchas personas es difícil de entender. Si se imaginan el recipiente en que Andrews hizo sus experimentos, lo que observarían es que arriba de P_c jamás podrían detectar el menisco que caracteriza la frontera entre las dos fases. También debemos advertir en este punto al lector sobre el uso del término "vapor" de una sustancia, muy utilizado en los ámbitos de la ingeniería. Se emplea para designar la fase gaseosa de una sustancia en aquella región de temperatura y presión donde la sustancia es licuable. Pero no representa una fase diferente, ni mucho menos, a la fase gaseosa: un vapor es el término empleado para describir a un gas que puede licuarse. Por último, queremos añadir que el diagrama p-V para el C0₂ es característico de todas las sustancias puras que pueden licuarse a presiones no muy elevadas como los gases nobles Xe, Ar, Ne y otras como el N₂, el O₂, el CH₄, CO, NH₃, etc. Hay dos características inescapables que se desprenden de la configuración de las isotermas y la separación respectiva de fases que exhibe la Fig. 17. La primera es que las sustancias reales difieren notablemente en su comportamiento al de un gas ideal cuya ecuación de estado es PV = vRT. De hecho ésta sólo se cumple a presiones muy grandes comparadas con la presión crítica y en regiones donde la densidad es muy pequeña, que para una masa constante de gas, corresponden a volúmenes muy grandes (r =M/V). La ecuación que describe a la presión como función de V y T en el intervalo de valores de la presión y la temperatura que abarquen una región significativa del plano p-V debe ser, pues, mucho más complicada. De hecho en la actualidad no hay una sola sustancia para la cual se haya determinado esa ecuación. Una medida de cuánto se desvía el comportamiento de un gas real de un gas ideal lo da el llamado factor de compresibilidad definido como

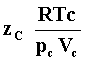
El valor de ésta cantidad sería uno si hubiese un gas ideal, licuable aunque éste no licua y por tanto no tiene un punto crítico (ver Fig. 16a) En la Tabla I listamos los valores de las variables termodinámicas en el punto crítico así como el valor de Zc para algunas sustancias.

Tabla I. Constantes críticas para algunas sustancias.

Sustancia	Presión crítica pc (en atmósferas)	Temperatura crítica Tc ñK	Volumen crítico molar Vc ml	Zc
He	2.26	5.2	60	3.18
H2	12.8	33.2	68	3.28
N2	33.5	126	90	3.42
CO2	73.0	304.2	95	3.68
O2	49.7	154.3	74	3.42
HCL	81.5	324.1	89	3.66
Cl2	76.1	417.1	124	3.63
SO2	77.6	430.3	125	3.64
CCl4	45.4	556.2	275	3.68
C6H6	47.9	561.6	256	3.75

Como se ve en esta tabla, el helio que posee la presión crítica más pequeña y el valor de Zc también más pequeño, dista mucho de poder concebirse como un gas ideal. Así pues, un criterio (no el único!) que debe imponerse a una ecuación de estado que pretenda describir el comportamiento de un fluido real es que dé lugar a un factor Zc que numéricamente concuerde con los resultados experimentales. A este respecto, vale la pena señalar que una de las áreas de la termofísica que mayores sorpresas ha proporcionado en los últimos veinticinco años ha sido precisamente el estudio de la materia en la vecindad de "puntos críticos", que como, Pc en la Figura 17, marcan el punto terminal de una región de coexistencia de fases. Las ideas clásicas que se tenían al respecto y que se originaron en 1872 debido al trabajo de J. D. van der Waals, consisten esencialmente en representar a estos puntos como aquellos en los cuales las funciones termodinámicas, presión, energía, etc. pueden expresarse en series de potencias de T-Tc, donde Tc es la temperatura crítica.¹⁵Debido a ello predicen un cierto comportamiento de otras variables termodinámicas como los calores específicos, la compresibilidad, la diferencia de densidades entre el líquido y el gas, etc. Pero se ha visto que este comportamiento no concuerda con el experimento. Consecuentemente, nuevas hipótesis al respecto nos han demostrado que estos puntos son "singulares" esto es las funciones termodinámicas no son desarrollables en series de potencias enteras alrededor de Tc, con lo cual surge el problema de visualizar y explicar cómo una función de T y V que genera curvas suaves y continuas como las que se exhiben en la Fig. 17 en todo el plano p-V puede cambiar su naturaleza y convertirse en una función "singular" en la vecindad del punto crítico. Este es uno de los tantos problemas asociados con un diagrama p-V, hoy en día no resueltos del todo.

Aunque es importante e interesante per se, el diagrama p-V no es la proyección de la superficie pVT que mejor se preste para discutir cómo esta información experimental puede analizarse con la ayuda de las leyes de la termostática, entre otras cosas, porque el papel de la fase sólida queda descartado. Para ello, es mejor usar la proyección en el plano p-T cuya forma para un fluido normal, esto es uno cuyo volumen disminuya al solidificar y está ilustrado en la Fig. 18.

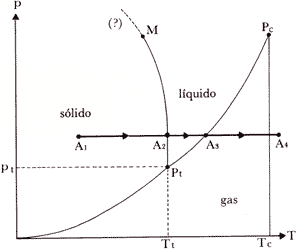
Figura 18. Diagrama p-T para una sustancia que se contrae al solidificar.

Sobre este diagrama se proyectan tres superficies que dan lugar a tres curvas, las cuales se intersecan en un punto común P_t llamado el punto triple. Como ya vimos este punto triple es invariante y lo determina la temperatura T_t¹⁶ y P_t, la presión del punto triple. Los valores de estas variables para algunas sustancias están dados en la Tabla II.

Las curvas OP_t, P_t P_c y P_tM se conocen, respectivamente, como las curvas de sublimación, de evaporación (o de ebullición) y de fusión. OP_t, la curva de sublimación, representa el conjunto de todos los puntos, esto es, parejas de valores de p y T en los cuales coexisten en equilibrio el sólido y el gas. Por ejemplo, un trozo de iodo metálico encerrado en un tubo en equilibrio con un gas.

Tabla II. Datos sobre el punto triple para varias sustancias

Sustancia	Tt (ñK)	Pt(mm de Hg)
He	2.172	37.8
H2	13.84	52.8
N2	63.18	94.0
O2	54.36	1.14
CO2	216.55	3880.0
SO2	197.68	1.256
H2O	273.16	4.58

La curva P_t P_c es de hecho la proyección de cada porción horizontal de las isotermas en la Fig. 17 en este plano, que corresponden a los valores de p y T a los cuales coexisten en equilibrio las fases líquida y gaseosa. Por ello es la curva ebullición. P_tM, la curva de fusión, es aquella que corresponde a los valores de p y T para los cuales la fase líquida y la sólida coexisten en equilibrio, por ejemplo hielo en equilibrio con el agua líquida a 4ñC. Las pendientes de las curvas de sublimación y de ebullición son siempre positivas, no así la pendiente de la curva de fusión. Para una sustancia que se expande al congelarse como el caso del agua la pendiente es negativa, que correspondería al caso opuesto del ilustrado en la Fig. 18.

Iniciemos una pequeña travesía a lo largo de la recta A₁ A₂ A₃ A₄ de la Fig. 18 pensando que en el punto inicial tenemos una muestra sólida de la sustancia a la temperatura correspondiente T_A1. Nótese que la presión va a permanecer constante y será mayor a la presión del punto triple p_t. Durante la porción A₁ A₂ de esta trayectoria, en la cual, como el lector puede percibir, se aumenta la temperatura, el calor empleado en hacerlo se gasta, para hablar en términos burdos, en ablandar al sólido. Al llegar al punto A₂ sucede una cosa interesante, muy similar a la observada en la porción horizontal de las isotermas en la Fig. 17

En efecto A₂ representa el punto para el cual a esa presión y la temperatura T_A2 las fases sólida y líquida coexisten. Así pues nos encontramos en este punto que si seguimos suministrando calor, la temperatura no se eleva hasta que todo el sólido se haya convertido en líquido. Para describir el fenómeno, nos imaginamos que el proceso es reversible y recurrimos a la ecuación (11),

Si llamamos DS = S_liq - S_sol, la diferencia entre las entropías del estado final (líquido) y del estado inicial (sólido),

DQ_rev = T (S_liq — S _sol. ) ñ l_ls

esto es, el calor transferido que se emplea en licuar al sólido es igual a la temperatura a la cual ocurre la transición multiplicada por la diferencia en las entropías de las dos fases. A este calor l_ls se le conoce como el "calor latente", en este caso, el calor latente de fusión. Si continuamos con nuestro proceso, ya habiendo fundido al sólido, a lo largo de la porción A₂ A₃ el calor transferido al líquido, se emplea en elevarse su temperatura hasta llegar a A₃. Obsérvese que A₃ es ahora un punto a lo largo de la curva CP_c de la Fig. 17. Si ahora suministramos más energía, ésta no aumenta la temperatura del líquido, sino que se gasta en su ebullición (curva CB Fig. 17), hasta convertir al líquido en vapor (gas). Suponiendo de nuevo que el proceso es reversible,

DQ_rev = T (S_liq — S _sol. ) ñ l_gl

donde l_gl es el calor latente de ebullición (o evaporación). El final de viaje es monótono pues de A₃ hasta alcanzar A₄, de nuevo, cualquier suministro de energía sólo sirve para aumentar la temperatura del gas.

En ambos cambios de fase, de sólido a líquido y de líquido a gas, hemos suministrado calor al sistema y por lo tanto, ambos l_ls y l_gl son cantidades positivas. En la tabla III mostramos algunos valores de ellos para varias sustancias. Esto implica que, en general, S_liq> S_sol. y S_gas>S_liq >o sea S_gas > S_liq > S_sol y este resultado merece cierta consideración. Si adoptamos el criterio discutido en el Cap. V que le asocia a S una medida del grado de desorganización de un sistema, diríamos que un gas está menos organizado que un líquido y éste que un sólido, lo cual incide con el hecho de que es más difícil, confinar un gas que un líquido y éste a su vez que un sólido. El grado de restricción es más pequeño en el gas que en el sólido (ñhay que comprimir para pasar de una fase a otra!). Pero también, la desigualdad S_gas > S_liq> S_sol. se utiliza para ilustrar el concepto de entropía como una medida del "desorden molecular", argumentando que en un sólido hay más orden (o menos desorden) que en un líquido y en éste a su vez más orden que en un gas.

Tabla III. Datos de fusión y evaporación para algunas sustancias.

Sustancia	Temperatura de fusión	Calor latente de fusión lsl julios/mol	Temperatura de ebullición Teñ K	Calor latente de evaporación llg julios/mol.
O2	54.4	444	90.2	6830.8
N2	63.2	722	77.4	5617.6
CO	68.1	838	81.7	6024.8
CH4	90.7	944	112.0	8210.3
C2H4	104.0	3350	170.0	13628.4
Kr	116.0	1640	120.0	9057.9

En tanto que el grado de restricción es un concepto que podemos cuantificar macroscópicamente, como ya discutimos con amplitud, la primera interpretación no está sujeta a vaguedades. Por otra parte, la segunda depende de un criterio un tanto subjetivo (ñy no definido!) sobre qué se entiende y cómo se mide "el orden o el caos molecular". Por ello es que preferimos la primera interpretación.

Vale la pena hacer notar también que como el camino A₁ ñ A₄ es reversible, si lo recorremos en sentido contrario, todo ocurre en sentido inverso a como hemos hecho el relato original y en este caso los calores latentes l_lg (de condensación) y l_sl (de solidificación) son liberados por la sustancia y numéricamente iguales a los de evaporación y fusión, respectivamente.

Finalmente, queremos hacer notar que hay otras características de las curvas que forman este diagrama que pueden ser obtenidas haciendo uso de las leyes de la termostática. Por ejemplo, se pueden obtener cuáles son las condiciones que deben satisfacer algunas de las funciones termodinámicas a lo largo de las curvas OP_t, P_t, P_c y P_tM, con objeto de establecer la condición de que las correspondientes fases coexistan en equilibrio, gas-sólido, líquido-gas y líquido-sólido, respectivamente. Ello permite calcular la pendiente de cada punto a lo largo de dichas curvas en función de los calores latentes, las densidades de ambas fases y la temperatura. Si además se conoce la dependencia de los calores latentes con la temperatura y de las densidades con la temperatura y la presión, se pueden obtener las ecuaciones explícitas de estas curvas, usualmente bajo la forma

log₁₀ p = A — — C log₁₀ T + DT

A, B, C, y D son constantes características de la sustancia de que se trata. Esta forma es típica para las curvas de sublimación (OP_t) y de evaporación(P_tP_c). La curva de fusión (P_tM) es la más difícil de obtener sobre todo, como lo indica el signo de interrogación en la Fg. 18, que el comportamiento de los sólidos a muy altas presiones todavía no es un fenómeno totalmente esclarecido. Ello implica que la forma de esta curva en su porción final es aún desconocida, tanto teórica como experimentalmente. Su entendimiento constituye todavía un reto a la física de la materia condensada.

NOTAS

15  La presión es una "función analítica" de la temperatura en la vecindad del punto crítico.

16  Es un punto invariante determinado por la temperatura Tt