VIII. LA BÚSQUEDA DEL CERO ABSOLUTO
UN LIBRO de esta naturaleza, no estaría completo si en alguna
forma, por elemental que sea, no se toca uno de los temas aparentemente más
complejos, atractivos y controvertidos, como es la llamada "búsqueda del cero
absoluto", o sea, el dominio de las regiones más frías alcanzada en la actualidad
por los seres humanos. Debemos advertir al lector que la relación que existe
entre el concepto tradicional de frío y el hecho de que lo asociamos con temperaturas
continuamente decrecientes es una mera coincidencia. En efecto, recordemos que
en el Capítulo IV establecimos la analogía entre la entropía
y la temperatura como variables que surgen de la necesidad misma, involucrada
en la especificación de atributos asociables a sistemas termodinámicos. Hablamos
entonces de la necesidad de establecer ciertas relaciones de orden. En el caso
de la temperatura, dicha relación está asociada a ordenar sistemas basados en
grados relativos de enfriamiento o calentamiento. La termometría, que es la
técnica que se adopta para realizar estas mediciones, tiene entre sus funciones
establecer una unidad de medición, el grado centígrado, el grado Fahrenheit,
etc. y determinar asimismo la "escala de temperaturas". Cuando un cuerpo se
calienta o se enfría alguna de sus propiedades varía con este proceso y esta
variación, referida a un estándar, sirve para determinar dicha escala.
Por razones estrictamente prácticas, de conveniencia, confiabilidad, reproducibilidad, facilidad, etc., se ha escogido una escala termométrica que es una función lineal de la variación de alguna propiedad y además, se ha escogido asociar una temperatura mayor con un mayor grado de calentamiento. Insistimos, ésta es nuestra elección, no un dictado de la naturaleza, y es debido a ella que las temperaturas más bajas están asociadas con los cuerpos más fríos. De haber procedido en otra forma estaríamos hablando de otro "número absoluto" y no del cero para designar el estado más frío del universo. Como por siglos hemos vivido bajo esta convención ya no nos sorprende correlacionar "frío" con "baja temperatura".
Después de este preámbulo, volvamos a nuestro tema, ¿por qué nos ha interesado la búsqueda del cero absoluto? Hagamos un poquito de historia. De nuestras discusiones en la última sección del capítulo anterior, puede apreciarse que la obtención de bajas temperaturas está íntimamente relacionada con el problema de la licuefacción de los gases y la solidificación de los líquidos, por lo menos hasta un cierto punto. Ya a principios del siglo pasado mediante la aplicación simultánea de altas presiones y cambios en la temperatura, varios gases como el CO2, el SO2, NH3 y otros, habían podido licuarse. El llamado "hielo seco" o CO2 sólido se obtenía permitiendo la evaporación del gas altamente comprimido y disminuyendo la temperatura. Cuando el CO2 sólido se mezcla con éter, se llega a obtener temperaturas tan bajas como -110ºC, procedimiento que permitió a M. Thilovier (1835) licuar gases como el etileno. Los experimentos de Andrews en 1869 constituyeron las bases sólidas detrás de los criterios necesarios para licuar un gas y de ahí surgieron los principios y las técnicas que permitieron a los químicos polacos Wroblewski y Olszewski en 1883 obtener oxígeno líquido a -136ºC y posteriormente licuar el N2 y el CO2 a -152ºC. En 1886 Dewar (inventor de los famosos frascos que hoy llevan su nombre) logró la producción continua de oxígeno líquido basándose en las ideas de Olszewski usando un método, llamado en cascadas en el cual cada paso se lleva a cabo por un licuefactor que esencialmente opera como un refrigerador doméstico.
El siguiente paso significativo en las técnicas de bajas temperaturas lo constituyó el famoso experimento de la pared porosa ideado por Joule y perfeccionado por Kelvin se le conoce como el efecto Joule-Kelvin. Este proceso fue la base de la licuefacción del aire llevada a cabo, casi simultáneamente por C. Linde en Alemania en 1895 y por W. Hampson en Inglaterra en 1896. En estos años, Dewar logró también licuar el hidrógeno alcanzando temperaturas cercanas a los -180ºC. Así es que a fines del siglo pasado las técnicas de licuefacción de gases permitían llegar cerca de los -200ºC, o sea 73 K, muy lejos del cero absoluto.
Pero en el año de 1908, usando también el efecto Joule-Kelvin, el gran físico holandés Heike Kammerlingh Onnes licuó el gas de helio alcanzando entonces la temperatura récord de 5.2 K (-267.8º C) y abrió con ello brecha para el desarrollo contemporáneo de la criogenia ( o ingeniería de bajas temperaturas) y de la física de bajas temperaturas. También fue el descubridor de la llamada "superconductitividad", esto es, la propiedad que exhiben varios metales puros y cientos de otros compuestos, de conducir la corriente eléctrica sin presentar prácticamente ninguna resistencia interna. Usando la técnica de K. Onnes para el mes de julio de 1926 todas las sustancias conocidas hasta entonces habían sido licuadas y solidificadas, incluyendo el helio. Decimos esto porque el helio es el único elemento conocido en la naturaleza que se mantiene líquido, a presión atmosférica, aun a temperaturas de 1ºK.
Para solidificarlo hay que someterlo a una presión de 25 atmósferas, a temperaturas menores a 1 K. Este descubrimiento se debió a H. Keesom, quién igualmente esclareció el diagrama de fases (el diagrama p-T) de este sorprendente elemento. En efecto, en 1932 Keesom y sus colaboradores descubrieron que a 2.19 K el helio (isótopo 4) sufre una transición de fase pero no a la fase sólida, sino a otra fase líquida. Entre las muchas propiedades, sorprendentes y fascinantes de esta fase líquida, le ha valido el nombre de "superfluido", se encuentra la de poder circular sin dificultad alguna por los capilares más estrechos concebibles, por donde el agua misma no lo puede hacer. En términos más llanos, es un fluido cuya viscosidad es prácticamente igual a cero.
Volviendo a nuestro tema principal, además del estudio de estos fascinantes fenómenos como la superfluidez y la superconductividad, la física de bajas temperaturas se enfrenta al reto de esclarecer el comportamiento de la materia a medida que la enfriamos más y más. Hoy en día la temperatura más baja que se ha alcanzado en un laboratorio es de 0.00005 K (5 x10 - 5 K) pero durante periodos de tiempo muy cortos, insuficientes para llevar a cabo experimentos. La temperatura más baja estable por un periodo de horas se ha obtenido en el hoy llamado Laboratorio de Bajas Temperaturas Kammerlingh Onnes de la Universidad de Leyden, Holanda, en el grupo que dirige el profesor G. Fosatti y es de 1.9 X 10 - 3 K (0.019 K). La búsqueda de la temperatura más baja alcanzable en el laboratorio, sea cual fuere su valor, es la que ha desatado controversias sobre, primero la posibilidad de llegar al cero absoluto y segundo, cuál es el valor de la entropía a esa temperatura. Discutamos estas cuestiones en un orden más lógico que cronológico.
Es muy común asociar, a la búsqueda del cero absoluto, la determinación del valor de la entropía a esa temperatura. ¿Por qué la entropía y no la energía o la entalpía u otra función termodinámica?, ¿por qué es justamente el valor de la entropía en el cero absoluto el que aparece como un factor preponderante en este tema? Permítame dar un par de razones para ello. Por una parte, está claro de la discusión histórica acerca de la obtención de bajas temperaturas, que por medio de algún dispositivo debemos extraer calor de un sistema, el que estamos enfriando para disminuir su temperatura. En otras palabras, retornando a nuestros primeros encuentros con máquinas térmicas, estamos haciendo uso de refrigeradores, lo que hizo precisamente la entropía con la variable asociada de manera natural con los procesos involucrados. Así por ejemplo, a lo largo de un proceso adiabático, como el proceso C2 C3 del ciclo Carnot (Fig. 5) la entropía permanece constante, en tanto que la temperatura disminuye. Si pensamos (¡idealmente!) en una secuencia de procesos que cada vez reduzcan más la temperatura, en cada uno de ellos la entropía será constante, pero no necesariamente la misma. Luego, esta constante, ¿tiende a un valor determinado a medida que nos aproximamos cada vez más al cero absoluto? ,
Por otra parte, en el último ejemplo sobre las aplicaciones termostáticas que mencionamos en el capítulo anterior, vimos, al estudiar el diagrama p-T de una sustancia pura que al pasar de la fase gaseosa de la sustancia a la fase sólida, (trayectoria A4 ® A1 de la Fig. 18) la entropía disminuye. Si ahora nos ubicamos en el punto A1 de la Fig. 18 y nos desplazamos a lo largo de la misma recta, la isóbara correspondiente, hacia la izquierda, esto es la región de bajas temperaturas, podríamos preguntarnos si la entropía sigue disminuyendo y finalmente tiende a un valor constante (¡que podría ser cero!) cuando la temperatura se aproxima al cero absoluto. Con estos dos argumentos el lector apreciará por qué es la entropía la variable natural para asociar el comportamiento de un sistema a medida que se le enfría continuamente.
A fines del siglo pasado y principios de éste surgieron además otras cuestiones,
más técnicas para ser abordadas aquí, que llevaron a muchos científicos a plantear
seriamente la posibilidad de determinar el valor absoluto de la entropía cuando
un sistema, cualquiera que éste sea, se lleva al cero absoluto. Entre otras
cosas, si se llegara a determinar este valor, quedaría resuelto el problema
de conocer la constante indeterminada que aparece en las definiciones, no sólo
de la entropía sino, como ya señalamos oportunamente, de la energía interna
y la entalpía. Haciendo uso de los datos experimentales disponibles, así como
de las predicciones teóricas que surgieron de la revolución cuántica, derivada
de los trabajos de Max Planck en 1900 y de Albert Einstein en 1905, otro físico
alemán, Walther Nernst propuso, en los albores de este siglo, que la entropía
debería comportarse de una manera determinada, cerca del cero absoluto. Más
específicamente, si llevamos a un sistema, cualquiera que éste sea, a las vecindades
del cero absoluto a lo largo de un proceso caracterizado por una variable, como
la presión en la Fig.18, que permanece constante en todo el proceso, entonces,
en el límite cuando T tiende a cero la diferencia de las entropías entre dos
estados cualesquiera caracterizados por la misma temperatura pero por diferentes
valores de la variable, e.g. la presión en nuestro ejemplo, tiende a
cero.
donde p1y p2 son dos presiones arbitrarias.
Esta afirmación, conocida como el principio de Nernst, difiere totalmente de la que podría inferirse de los procesos ejemplificados en la Fig. 18 para los cuales la conclusión mas lógica sería aceptar que a lo largo de cada trayectoria S disminuye hasta alcanzar un valor finito quizás cero, al llevar al sistema cerca del cero absoluto. Esto implicaría que
La diferencia entre ambas conclusiones está claramente exhibida en las Figuras 19 y 20 en las cuales, arbitrariamente hemos tomado a la presión como la variable que está parametrizando el proceso y hemos graficado en un diagrama T-S, las dos posibilidades.
Vale la pena mencionar, aunque sea sin dar la demostración, que el caso mostrado
en la Fig. 19 se cumple si la capacidad calorífica a presión constante se hace
cero cuando T tiende a cero. Dado que esta cantidad es medible en el laboratorio
se ha podido corroborar que esto ocurre en todos los sistemas conocidos. En
el segundo caso, Fig 20, no basta con que esta propiedad se satisfaga para que
DS = O en T = 0ºK. En este sentido el postulado de
Nernst es más fuerte que la sola condición de que Cp tienda a cero
cuando T se aproxima al cero absoluto.
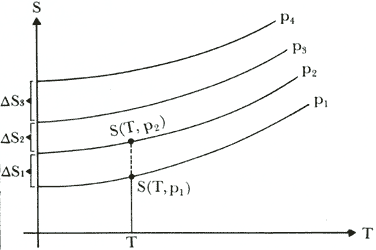
Figura 19. Curvas para un sistema parametrizadas por p mostrando el caso en que DS es finito en el cero absoluto.
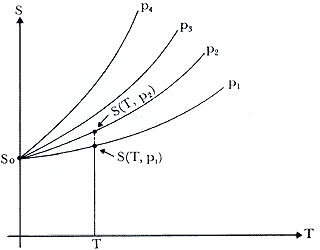
Figura 20. Curvas para un sistema, parametrizadas por la
presión p mostrando el postulado de Nernst DS = 0
en el cero absoluto (¡ pero no S !).
Todavía en el año de 1911, Max Planck intentó darle un carácter universal a la constante S0 que aparece en la Fig. 20 postulando que la entropía de todo sistema tiende al valor cero cuando T tiende a cero, v.gr. S0 = 0.
Es importante señalar en este momento, que cualquiera que sea el caso, la única forma de comprobar cuál es la situación correcta es mediante el experimento. Varios modelos microscópicos de la materia corroboran el hecho de que a medida que nos acercamos al cero absoluto, la capacidad calorífica pertinente tiende a cero, lo cual está de acuerdo hasta el momento, con las mediciones experimentales que se han logrado hacer a las temperaturas más bajas, del orden de los milikelvins 10 - 30K). Como la entropía no puede medirse directamente, su conocimiento se obtiene a partir de dicha capacidad calorífica. Por ejemplo, en el caso de Cp,
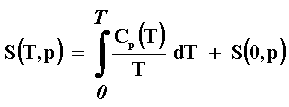
de ahí entonces que hasta hoy en día este es el único método confiable disponible para conocer la entropía a bajas temperaturas. Todo parece coincidir con el principio de Nernst que establece la condición adicional de que S(0, p) debe ser igual a una constante S0 , pero no necesariamente cero. Esta "entropía residual" en el cero absoluto, cuyo valor es diferente para cada sistema, se interpreta como proveniente de algún grado de libertad que se quedó congelado en el proceso de enfriamiento y consecuentemente impidió la formación de un verdadero estado de equilibrio. Estos estados, llamados "metaestables", son frecuentes en materiales muy viscosos como por ejemplo los varios tipos de vidrios. Pero, lo importante de esta discusión es apreciar que cualquiera que sea la razón, su explicación está fuera del dominio de la termostática, es necesario recurrir a los modelos microscópicos de sistemas formados por muchas moléculas, i.e., a la llamada mecánica estadística cuántica.
Con base en esto F. Simon en 1937 propuso modificar el enunciado original de
Nernst para llegar a lo que ahora se conoce como principio de Nernst-Simon:
Llegamos así al final de nuestra discusión planteando la pregunta: ¿tiene sentido hablar de una tercera ley de la termostática? Obsérvense dos cosas: hemos evitado hablar del principio de Nernst como una ley y segundo, las leyes primera y segunda son manifestaciones claras y concisas sobre imposibilidades de la materia. En este sentido el principio de Nernst-Simon no expresa una imposibilidad similar. Por estas razones Nernst mismo en l912 y después muchos otros investigadores de la física de bajas temperaturas dieron un enunciado diferente al principio de Nernst que tiene, por lo menos en cuanto a semántica, la forma de una imposibilidad y que ahora se le conoce como la inalcanzabilidad del cero absoluto: "Es imposible reducir la temperatura de un sistema termostático al cero absoluto en un número finito de operaciones."
El debate actual radica precisamente sobre si este enunciado debe elevarse a la jerarquía de una ley y consecuentemente adoptarlo como la Tercera Ley de la Termostática.
Para sostener la candidatura se ha buscado demostrar que este principio es equivalente al principio de Nernst-Simon. Los oponentes arguyen que la afirmación es una tautología, esto es, demostrar que una verdad es equivalente a otra.
No podemos entrar aquí en los detalles técnicos pero la imagen gráfica del
argumento es muy simple y está basado en las Figuras 19 y 20. En efecto, si
el principio de Nerst-Simon no se cumple, Fig. 19, el cero absoluto es un número
finito de operaciones. En efecto, en la Fig. 21 vemos que a partir de un estado
inicial dado S(Ti, pi) una sucesión de procesos,
uno adiabático AB, seguido de otro isotérmico BC, etc., nos conduce
al cero absoluto. Esto es claramente consecuencia de que DS
es finita en T =0ºK. Recíprocamente, si el cero es alcanzable sólo puede hacerse
si DS es finita.
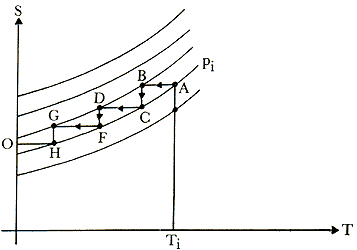
Figura 21. A partir de un estado inicial arbitrario S(Ti, pi ) el cero absoluto
es alcanzable a través de la sucesión de proceso A,B,C,D,F,G,H,O.
En cambio, si se satisface el principio de Nernst-Simon, independientemente
de cuál sea el valor de S0, para llegar al cero necesitamos de un
número infinito de operaciones como se ilustra en la Fig. 22. A medida que nos
vamos acercando al cero los escalones isotérmicos se van haciendo cada vez más
pequeños pero se necesita una infinidad de ellos para llegar al cero.
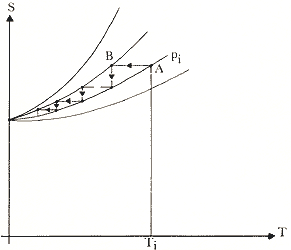
Figura 22. A partir del punto A a la presión Pi, el cero absoluto es inalcanzable en un número finito de operaciones.
Estos argumentos lógicos, coherentes y simples convencen a los partidarios de la Tercera Ley y la aceptan como tal. Pero hay una objeción que consiste en definir los peldaños adiabáticos A B, C D, etc. Para que el proceso reversible AB sea posible la entropía del estado B tiene que ser mayor o igual que la entropía del estado A y por consiguiente para definir dicho proceso necesitamos conocer las entropías, a priori, que sólo las podemos obtener de la ecuación (37).
Para ello tenemos que poseer información extratermodinámica, esto es, conocer
los valores teóricos o experimentales de Cp en este caso y
de S0 . Una vez que los tenemos, todo lo que estamos probando
es que si el proceso AB puede ocurrir entre dos temperaturas finitas,
también ocurre a 0ºK con valor DS
= 0. Las otras dos leyes están totalmente libres de este tipo de objeciones
por lo cual muchos autores, incluyendo al de esta obra, no consideran que la
inalcanzabilidad del cero absoluto deba ser elevada a la jerarquía de una ley.
Además insistimos, el cero mismo es producto de una escala arbitraria para medir
temperaturas, no es una propiedad universal de la materia.

El conde de Rumford (1753-1814). Grabado de Joseph Rauchmayer hecho en 1797.







Jaime Watt.