APÉNDICE A

En este apéndice queremos probar que ninguna máquina térmica operando entre dos cuerpos o fuentes térmicas puede tener una eficiencia mayor que la de una máquina de Carnot operando entre dichas fuentes. Es muy importante que el lector aprecie que la afirmación sólo es válida para la operación entre dos cuerpos o fuentes térmicas. Llamemos C a la máquina de Carnot y M a la otra. Como C es reversible por ser de Carnot suponemos que absorbe el trabajo generado por M, W_M (Fig. 23). Esto es, M opera a C como un refrigerador. Sea Q_M el calor que M toma del cuerpo a temperatura T₂ y Q_c el calor que le regresa C. Las eficiencias de M y C como máquinas térmicas son:

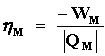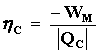Si suponemos que h_M > h_c cómo los numeradores son iguales, forzosamente ñQ_Mñ < ñQ_cñ, esto es, el calor absorbido por M es menor que el cedido por C. Como además por la ecuación (5)

— W_M = ñQ_Mñ - ñQ_Mñ = ñQ_cñ - cñQñ_cñ

el conjunto de las dos máquinas M y C, operando en ciclos, no hacen otra cosa más que extraer una cantidad de calor ñQñ_cñ - ñQñ_Mñ del cuerpo frío y llevarlo al cuerpo caliente (puesto que es igual a ñQ_cñ - ñQ_Mñ ). Esto viola el enunciado de Clausius para la segunda ley y por lo tanto

h_M ñ h_c   q.e.d.

Esto es válido para cualquier máquina térmica M ñsea o no reversible! Dejamos al lector probar que si es reversible entonces h_M = hc.

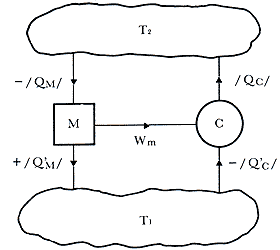
Figura 23. El principio de Carnot afirma que si C es una máquina de Carnot y M otra máquina cualquiera, ambas operando entre dos temperaturas T₁ y T₂, T₂ > T₁ entonces h_M ñ h_c