III. EL CAMINO HACIA LA SEGUNDA LEY. LA ENTROPÍA
EN EL capítulo II hemos discutido con bastante detalle
el trabajo que realizó Carnot para formular la teoría subyacente al funcionamiento
de las máquinas térmicas. Sus resultados fundamentales son que para operar una
máquina térmica eficientemente, basta utilizar sólo dos cuerpos a temperaturas
tales que la de un cuerpo sea mayor que la del otro y operar la máquina, con
cualquiera que sea la substancia operante, en ciclos de manera que en sólo dos
de los procesos de cada ciclo dicha substancia intercambie calor con dichos
cuerpos. Cuando está en contacto con el de temperatura mayor, absorbe de él
una cierta cantidad de calor y cuando está en contacto con el de temperatura
menor le cede otra cantidad de calor. Esta operación minimiza las pérdidas de
calor por diferencias de temperatura espurias y además, como al final del ciclo
Uf = Ui, la energía interna de la substancia operante es la misma que cuando
empezó. Por lo tanto el trabajo neto realizado en el ciclo es
|
W = Q2 - Q1
|
donde Q2 es el calor absorbido del cuerpo caliente y Q1 es el calor cedido al cuerpo frío con la convención (¡arbitraria!) de que Q es positivo para un sistema cuando absorbe calor y negativo si lo cede. La ecuación (5) es pues una consecuencia directa de la (3). La representación gráfica de este proceso se da en la Fig. (2) donde los cuerpos están representados por rectángulos con las paredes estriadas y la máquina térmica por un círculo con la letra C, si pensamos que es una máquina de Carnot.
El segundo resultado importante que obtuvo Carnot, y cuya demostración está basada en la concepción errónea sobre el calor (pensaba en él como el calórico), fue demostrar que ninguna máquina operando entre dos cuerpos a temperaturas diferentes puede ser más eficiente que la máquina concebida por él (véase Fig. 3).
Sin embargo, a pesar de que planteó la cuestión de como calcular la fracción de calor que es aprovechable para convertirse en trabajo mecánico y de expresarla en términos de las temperaturas de los cuerpos entre los cuales opera la máquina, nunca obtuvo su expresión matemática. Como hicimos notar al final del capítulo I Carnot mostró que el trabajo W sólo depende de las temperaturas de ambos cuerpos pero, repetimos, no obtuvo la relación explícita entre estas cantidades. Este problema fue resuelto en 1854 por R. Clausius a quien, además, puede considerarse como el hombre que realmente concibió en forma matemática las dos primeras leyes de la termostática. Pero antes de estudiar el trabajo de Clausius hablemos más del ciclo que sufre una substancia en una máquina de Carnot, así entenderemos mejor la discusión subsecuente.
Pensemos en los procesos numerados del 1) al 6) que describen la máquina de Carnot y al aire, la substancia operante que él eligió, como un gas ideal. Puesto que un gas ideal obedece la ecuación de estado, esto es la relación entre las variables p,V y T, bien conocida por todos
|
p V = v RT
|
(6)
|
donde v es el número de moles y R una constante conocida como
la constante universal de los gases,3podemos
visualizar el ciclo que sufre el aire en el ciclo de Carnot si graficamos los
diferentes procesos en un sistema de ejes cartesianos donde p es la ordenada
y V la abscisa (espacio de estados termodinámicos). Sea V1 el volumen
del aire cuando el pistón está en su posición inicial cd ocupando el volumen
abcd del cilindro. Denotemos por p1 la presión correspondiente. Esta
pareja determina un punto en el plano p-V que denotaremos por C1.4
Después de la primera expansión que ocurre en contacto con el cuerpo A a la
temperatura TA durante el cual el aire absorbe de dicho cuerpo una
cantidad de calor que denotaremos por +QA, alcanza el volumen abef
en el cilindro. A este volumen lo llamaremos V2; a la presión correspondiente
p2 y C2 al punto que definen en el plano PV. Ahora podemos
determinar la forma de la curva que une C1 con C2, pues
durante todo este proceso TA es constante y de acuerdo con la ecuación
(6) p V = vRTA = const. La curva PV = const. determina una
hipérbola equilátera que pasa por C1 y C2 (ver Fig. 5).
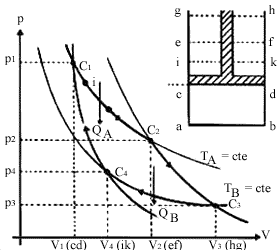
Figura 5. La representación geométrica del ciclo de Carnot en un plano p-V cuando
la sustancia operante es un gas ideal. QA es el calor absorbido y
QBel calor cedido. ( Los puntos C1, C2, C3
y C4 corresponden a los señalados en el diagrama de la derecha.)
Subsecuentemente (paso 3) el cuerpo A se retira de su contacto con el gas, pero éste procede a expandirse hasta ocupar el volumen marcado por ghab en el cilindro y que denotaremos por V3; p3 es la presión correspondiente y C3 el punto en el plano. La curva que une los puntos C2 y C3 representa un proceso en el cual la sustancia operante no absorbe (ni cede) calor en los alrededores, lo que se conoce como un proceso adiabático. La curva correspondiente tiene una ecuación un poco más complicada que la ecuación de las isotermas (curvas sobre las cuales T = cte) pero que no necesitamos aquí. Sólo basta con saber que C2 y C3 están sobre una de ellas. En el proceso subsecuente, el aire se pone en contacto con el cuerpo B a la tempertatura TB < TA y se comprime hasta ocupar el volumen abik. Al igual que en el primer proceso, TB es ahora constante pero como el gas se comprime tiene que ceder al cuerpo B una cantidad de calor QB para mantener su temperatura constante. Llamemos V4 al volumen abik, p4 la presión correspondiente y C4 el punto que estas dos coordenadas definen en el plano. En el último proceso se remueve el cuerpo B de su contacto con el aire y éste se continúa comprimiendo hasta regresar al punto de partida C1. En esta última etapa, el aire no absorbe ni cede calor; esto es, el proceso es adiabático y con ello se completa el ciclo.
De acuerdo con la ecuación (5) el trabajo neto realizado por el gas (la sustancia operante es aire en este caso) es W = QB - QA.
Es ahora muy fácil hacer ver que este trabajo neto es igual al área cerrada
por el ciclo C1 C2 C3 C4, esto es,
el área delimitada por las dos isotermas y las dos adiabáticas en la Fig. (5).
En efecto, veamos qué ocurre con el gas en el cilindro durante cada etapa. Consideremos,
por ejemplo el inicio de la expansión de C1 a C2. En C1
el gas ocupa el volumen abcd. Si efectuamos un desplazamiento inicial muy pequeño
por una distancia dx medida sobre la pared lateral del cilindro, la fuerza ejercida
por el gas (aire) sobre el pistón es la presión p1 por el área del
cilindro A, esto es p1A. El trabajo realizado, fuerza por distancia,
es p1 = Adx pero Adx = dV, el incremento en el volumen del gas, el
trabajo es p1dV. Si queremos obtener el trabajo total ejercido por
el aire sobre el pistón tenemos que sumar todas las contribuciones pidV donde
pi denotaría la presión en un punto i sobre la curva y cuyo valor no
es el mismo en cada punto pues depende del volumen Vi de acuerdo
con la ecuación (5), esto es Pi Vi = const. Pero esto
es irrelevante para el resto del argumento puesto que si aplicamos el mismo
razonamiento sobre los cuatro procesos que constituyen el ciclo, vemos que el
trabajo total W es la suma algebraica de las contribuciones sobre cada trayectoria,
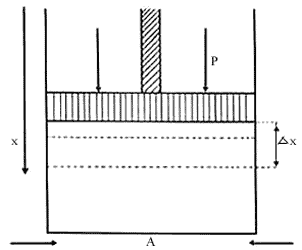
Figura 6. Cada vez que realizamos un desplazamiento Dx
del pistón, la fuerza es P. A y el trabajo es p. A. Dx
= pDV× DV
= ADX es el volumen del gas comprimido.
Esta cantidad puede escribirse como5
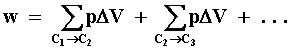
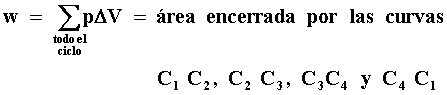
donde la última igualdad proviene de suponer que los incrementos en el volumen
DV son muy pequeños. En este caso la sumatoria se
puede reemplazar por una integral y finalmente recurrir a la interpretación
geométrica de una integral que representa el área bajo una curva. Si denotamos
por el símbolo§ ésta integral alrededor del ciclo, finalmente tenemos que
Esta fórmula tan sencilla nos dice que el trabajo neto realizado por la sustancia operante, el aire en este caso, es igual al área encerrada por las curvas que definen los procesos constituyendo el ciclo que en este caso es el ciclo de Carnot. Con la ayuda de esta discusión podemos volver ahora a la respuesta que dio Clausius respecto a la obtención de una fórmula que permita calcular la fracción máxima de calor Q que es aprovechable como trabajo mecánico. Claramente, cualquiera que sea la respuesta, debe ser consistente con el principio de la energía, que en este caso, está expresado por la ecuación (5) con Q2 = QA y Q1= QB. La hipótesis crucial de la cual partió Clausius fue suponer que el proceso a que está sujeta la substancia operante en una máquina térmica, v.gr., una máquina de Carnot, es un proceso "ideal". Por ideal Clausius entendía de hecho lo mismo que Carnot, esto es, que el proceso pudiese realizarse en los dos sentidos.
En la terminología moderna esto quiere decir que el proceso es "reversible"
y la idealidad realmente estriba en que la reversibilidad implica que se lleve
a cabo muy lentamente para que en cada estado intermedio por el que pasa el
sistema, alcance un estado de equilibrio y además no haya pérdidas de energía
por fricción. Esta última consideración es la más importante, pues si existen
estas pérdidas en una dirección las hay en el sentido opuesto en cuyo caso el
proceso no es reversible pues algún agente externo tendrá que compensar
la energía perdida en sobreponerse a dicha fricción. En seguida, Clausius hizo
notar que para un proceso "ideal", el calor Q que recibe o cede la substancia
operante de un cuerpo a una temperatura T, permanece constante durante todo
el proceso. Si ahora, definimos la eficiencia de una máquina térmica como el
trabajo que produce dividido entre el calor que recibe de un cuerpo u otra fuente
cualquiera, y convenimos en asignarle un signo positivo al trabajo recibido
por un sistema y un signo negativo al trabajo realizado por el sistema sobre
sus alrededores, la eficiencia n del ciclo de Carnot
está dada por
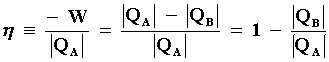 |
(7) |
Por otra parte, por construcción, el ciclo de Carnot es "reversible" esto es,
ideal según Clausius, luego
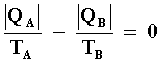 |
(8) |
pues en los dos procesos adiabáticos el sistema (aire) no intercambia calor con sus alrededores. Además la suma total es cero puesto que el cociente de Q entre T para cada proceso es independiente del proceso y, como U, sólo depende de los estados de la substancia operante. Como el proceso es cíclico y el aire regresa a su estado inicial el cambio neto de Q /T al final del proceso debe ser cero. Substituyendo la ecuación (8) en (7) obtenemos la famosa y deseada expresión para la eficiencia máxima de una máquina térmica operando entre dos cuerpos,
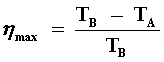 |
(9) |
Es preciso subrayar que la definición (7) es completamente general en tanto
que la ecuación (8) sólo es aplicable a procesos reversibles, de ahí
que la ecuación (9) constituye la eficiencia máxima. Como TA
< TB, hmax < l, esto es , aun para
procesos ideales no hay máquinas cien por ciento eficientes operando entre dos
temperaturas. Este resultado se aclara si reconocemos que a pesar de la idealidad,
el calor QB que se desecha al cuerpo frío representa una energía no aprovechada.
Además, la ecuación (9) representa la expresión matemática de la proposición
fundamental de Carnot enunciada al final del cap. II e.g. El trabajo
aprovechable sólo depende de la temperatura de los dos cuerpos entre
los cuales funciona la máquina y no de los agentes encargados de producirlo.
Pero veamos una cuestión que indudablemente no podemos pasar por alto, a saber, el significado de la hipótesis de Clausius. Él afirma que en todo proceso reversible e isotérmico (temperatura constante) el cociente de Q/T no depende del proceso sino sólo depende de los estados final e inicial, ambos forzosamente de equilibrio, pues el proceso es reversible, y ambos estados referidos a la substancia operante. Precisamente, como en el caso de la energía interna, esta aseveración implica que dicho cociente es una propiedad inherente del sistema, un atributo que está en la misma jerarquía que p, V, T, U, etc. Si acordamos en designar a este atributo con la letra S, su cambio entre dos estados, el final y el inicial i, está dado por
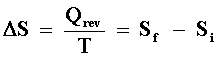 |
(10) |
donde el símbolo Qrev pone énfasis en el hecho de que la ecuación (10) se cumple sólo en procesos reversibles.
Es por ello que en el ciclo de Carnot DS = O y de ahí se extrae la ecuación (8). En este punto, conviene señalar que contrario al significado físico de U, que es por lo menos intuitivamente obvio por nuestro contacto cotidiano con la energía, el significado de S dista mucho de manifestarse, ni siquiera vagamente. Todo lo que podemos decir, hasta el momento, es que es una función útil en el estudio de la eficiencia de las máquinas térmicas. Sobre esto y cuestiones relacionadas, seguiremos insistiendo a lo largo del texto.
Por el momento, regresemos a la ecuación (10) para abordar una pregunta que seguramente ya está en la mente del lector: ¿Qué pasa si el proceso no es ideal, e.g., no es reversible? (¡esto implica que no podemos descartar la fricción!). Lo que observó Clausius es que en estos casos, que corresponden a los procesos reales, el cambio en la función S es mayor que el cociente Qrev./T. Esto lo llevó a proponer que para cualquier proceso que tenga lugar entre dos estados de equilibrio de un sistema dado, la relación
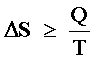 |
(11) |
donde Q es el calor transferido entre el sistema y el cuerpo o el medio ambiente, con el cual esté en contacto y se encuentra a la temperatura T.6 Esta relación, quizás la más controvertida, mal comprendida y abusada de toda la termostática, y cuya validez dentro de un contexto perfectamente bien definido ha sido incuestionablemente establecida, es una forma de expresar la segunda ley de la termostática. Obviamente, el signo igual en (11) se cumple cuando el proceso es uno ideal y reversible.
Antes de pasar a discutir y analizar a fondo el significado y dominio de validez de la ecuación (11), así como de intentar buscar una interpretación de esta función S, veamos algunas de las consecuencias más inmediatas y notables de estos conceptos propuestos por Clausius.
El primero de ellos concierne a la utilidad de la definición de la eficiencia n y su conexión con la aseveración manifestada por Carnot acerca de que no existe otra máquina térmica que, operando en ciclos reversibles entre dos cuerpos a diferentes temperaturas, sea más eficiente que la máquina de Carnot. En efecto, usando la definición propuesta h y dada por la ecuación (7) es relativamente fácil probar esta afirmación, si antes reconocemos otra forma de enunciar la segunda ley de la termostática también debida a Clausius.
Recordemos que el ciclo por el cual se lleva al aire (u otra sustancia operante)
en el ciclo de Carnot, es reversible; esto es, puede operar en una dirección
para producir trabajo o en la dirección opuesta, como refrigerador, para transferir
calor del cuerpo frío al cuerpo caliente. Pero esta última operación requiere
forzosamente de la participación de un agente externo que proporcione el trabajo
necesario. Clausius hizo notar que sin el concurso de este agente externo la
operación es imposible y propuso un axioma:
Note el lector la frase "no haga otra cosa" la cual implica que al final del ciclo la sustancia operante haya regresado a su estado inicial y cualquier otro cuerpo, máquina o dispositivo que participe en esta operación, no haya sufrido cambio alguno. La máquina a que se hace referencia en el axioma de Clausius se conoce como un perpetuum mobile de segunda clase y el axioma mismo, que constituye el enunciado de la segunda ley de la termostática, lo que hace es prohibir su existencia. Hasta hoy en día la validez del axioma es incuestionable.
El principio de Carnot es fácil de probar. Sólo es necesario mostrar que de existir una máquina reversible operando entre dos cuerpos a temperaturas dadas, una mayor que la otra, con eficiencia mayor que la de una máquina de Carnot operando entre dichos cuerpos, constituye una violación al axioma de Clausius. El detalle de la demostración la encuentra el lector en el Apéndice A al final del libro.
A estas alturas nos encontramos con que tenemos ya dos formulaciones, aparentemente
independientes, una expresada por la desigualdad (11) y otra por el axioma de
Clausius. La conexión entre ambas es también relativamente fácil de establecer
de manera cualitativa y dicha conexión se conoce como el teorema de Clausius.
Si incluimos el signo algebraico que le corresponde a cada valor de Q en la
ecuación (8) podemos reescribir esta ecuación como
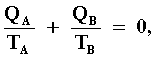
donde QB = ¾ ½QB½.
Imagine ahora el lector un ciclo reversible arbitrario representado por la línea
sólida cerrada en el diagrama p-V de la Fig. 7. En este diagrama consideremos
que dicho ciclo puede aproximarse por la suma de un número arbitrariamente grande
de ciclos Carnot de manera que cada porción del ciclo y su porción opuesta correspondan
a las dos trayectorias adiabáticas de uno de los ciclos de Carnot. Como la ecuación
(8) vale para cada ciclo de Carnot que sólo involucra la absorción de calor
a la temperatura mayor y la emisión de calor a la temperatura fría, al sumar
sobre todos los pasos isotérmicos de ciclos tenemos que
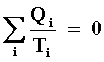 |
(12) |
aquí S es una operación que indica que es
necesario sumar sobre todas las isotermas que describen a los ciclos de Carnot
usados para imitar al ciclo original. Como esta imitación puede ser arbitrariamente
precisa, cuanto más fina sea la subdivisión en isotermas y adiabáticas, utilizando
de nuevo el símbolo ![]() para
indicar esta sumatoria cuando tomamos porciones infinitesimales, tenemos que
para
indicar esta sumatoria cuando tomamos porciones infinitesimales, tenemos que
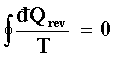 |
(13) |
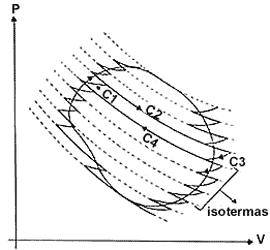
Figura 7. Un ciclo reversible en el cual cada porción está aproximada por
una adiabatica comprendida entre dos isotermas vecinas de manera que esa porción
y su parte opuesta formen parte de un ciclo de Carnot (ej.: el ciclo C1,C2,C3,C4).
La ecuación (13), válida sólo para un ciclo reversible y de ahí la notación
![]() Qrev, es una parte
del teorema de Clausius. Este argumento tan simple y poderoso muestra entonces
que la cantidad
Qrev, es una parte
del teorema de Clausius. Este argumento tan simple y poderoso muestra entonces
que la cantidad
es tal que para cualquier ciclo reversible, ya no sólo uno de Carnot, su valor
al iniciarse el ciclo es igual al finalizar el ciclo y por lo tanto esa función
S no depende del proceso cíclico. Si el ciclo es uno arbitrario y no
necesariamente reversible, Clausius mostró que, si el axioma arriba enunciado
debe satisfacerse, entonces
 |
(14) |
lo cual establece la conexión entre dicho axioma y la ecuación (8). La demostración
de la ecuación (14) está fuera de los alcances de esta exposición pero el lector
interesado puede encontrarla en prácticamente cualquier texto sobre los principios
de la termodinámica clásica. Para finalizar con esta discusión sobre cómo la
debatida cuestión acerca de la conversión de calor en trabajo útil llevó a Carnot
a discutir su máquina ideal y cómo de ella Clausius formuló la segunda ley,
es necesario mencionar un enfoque independiente del problema que en 1851 llevó
a William Thomson, lord Kelvin, a proponer una tercera versión de la segunda
ley de la termostática. Regresando a la máquina de Carnot y en particular a
la fórmula para su eficiencia dada por la ecuación (7), Kelvin hizo notar que
de no existir pérdidas de calor algunas en el proceso, incluyendo la transferencia
de calor de la máquina al cuerpo frío, esto es |QB|
º 0 se tendría una máquina perfecta, o sea una
máquina para la cual su eficiencia sería 1 (h =1).
¡Esto sería fantástico! Podríamos operar toda la maquinaria de un trasatlántico
con sólo extraer calor de las aguas del océano sin nunca afectar su temperatura.
Y una situación similar para un vehículo aéreo que sólo extrajera calor de la
atmósfera. Más tales dispositivos no existen. De ahí el enunciado de Kelvin:
Este enunciado es completamente equivalente al enunciado de Clausius, pues es posible demostrar que si uno supone la violación de uno de ellos, automáticamente se viola el otro, y recíprocamente. Puesto que esta demostración sólo requiere del uso de la lógica elemental, la hemos incluido en el Apéndice B.
En términos más llanos, la primera ley prohibe la existencia de máquinas de movimiento perpetuo de primera clase, esto es, máquinas cuya única función sea la de crear o aniquilar energía; la segunda ley prohibe la existencia de máquinas de movimiento perpetuo de segunda clase, esto es, cien por ciento eficientes. Por tanto, el mundo de los procesos en que están involucrados transformaciones de energía está regido por dos leyes las cuales podemos ahora resumir en términos todavía más simples:
Primera ley: En los procesos que involucran transformación de energía, sólo podemos salir a mano.
Segunda ley: En tales procesos, ni siquiera podemos salir a mano, o en pocas palabras, nunca podemos ganar ni salir a mano.
NOTAS
3 R = 8.3149 x 103 julios/kg-molºK = 1.982 cal/g-molºK
4 Advertimos al lector que esta secuencia corresponde a la Fig. 5 y no a la Fig. 3.
5 S (sigma mayúscula) es un símbolo usado para indicar "sumatoria sobre ". En este caso la suma es sobre todas las contribuciones pDV a lo largo de cada trayectoria.
6 Para los lectores más avezados a los métodos
matemáticos, si el proceso es infinitesimal, dS ![]() Q/T
donde
Q/T
donde ![]() es
un símbolo que puntualiza que Q no es una variable de estado.
es
un símbolo que puntualiza que Q no es una variable de estado.