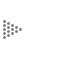IV. EL CONCEPTO DE ENTROPÍA
ESTE capítulo está dedicado a la discusión de la ecuación (11), la cual, como hicimos notar en el párrafo siguiente a su planteamiento, es la ecuación más controvertida de toda la termostática. En dicha ecuación aparece la variable S la cual, como hemos precisado e insistido en el capítulo anterior, desempeña un papel primordial en la teoría de las máquinas térmicas y en particular en dar una respuesta a una pregunta de índole estrictamente práctica, la máxima fracción de calor convertible en trabajo útil.
Así pues, es preciso reconocer el origen estrictamente utilitario de S cuyo
significado, es además, por el momento totalmente misterioso. En 1865, casi
once años después de haberla introducido a la termodinámica, Clausius escribió
un trabajo en el cual estudió esta función para varios sistemas. En dicho estudio
pudo apreciar el papel importante de S en las transformaciones de diferente
naturaleza y de ahí la llamó "entropía" (del griego tropos, que significa cambio,
transformación). Como último párrafo del trabajo, Clausius escribió:
Por el momento me limitaré a mencionar el siguiente
resultado: si imaginamos la misma cantidad, que en el caso de un sólo
cuerpo he llamado su entropía, compuesta en forma consistente para todo
el Universo (tomando en cuenta todas las condiciones), y si al mismo tiempo
usamos al otro concepto, energía, con su significado más simple, podemos
formular las leyes fundamentales del Universo correspondientes a las dos
leyes de la teoría mecánica del calor en la forma simple siguiente:
|
Con esto termina su trabajo sin que jamás explicara ni en él, ni en otro trabajo posterior, el significado de las frases "en forma consistente" ni "tomando en cuenta todas las condiciones". El abuso y mal uso que se le ha asociado a la entropía, proviene, en opinión del autor, de una concepción equivocada y extralimitada de esta ambiciosa versión universal de las leyes de la termostática.
Por último, los divulgadores y muchos profesionales de la ciencia, a falta de una concepción clara del concepto fenomenológico de S han recurrido a modelos moleculares de la materia para interpretar S como una medida del "desorden" molecular, en muchos casos sin precisar antes cual es, a este nivel, el concepto de orden. Aunada a esta versión ajena al mundo macroscópico, también suele asociarse a la desigualdad (11) una dirección en el tiempo de los procesos reales (ñno reversible!). Así pues la bibliografía abunda en por lo menos tres versiones sobre la "conceptualización" de la entropía:
1) Una medida de la "disponibilidad" de convertir calor en trabajo. (Versión muy socorrida en ingeniería.)
3) Una medida de la dirección de los procesos naturales.
Emprendamos pues un largo, pero ameno, camino para ver en que forma la ecuación
(11) realmente arroja luz sobre el significado físico de la función S. Omitimos
el punto 1 pues ya está ampliamente discutido en el capítulo anterior. Recordemos
primero que cuando se cumple la igualdad 
nos estamos refiriendo al cambio en la entropía entre dos estados de un sistema,
ambos estados de equilibrio, entre los cuales ocurre un proceso tal que cada
estilo intermedio es también uno de equilibrio. Es decir, el proceso es reversible
y durante dicho proceso el sistema sólo intercambia calor DQ
con un sólo cuerpo a la temperatura T, que es la misma durante todo el proceso.
En otras palabras estamos hablando de un sistema que sólo intercambia calor
con otro cuerpo, que bien pueden ser sus alrededores, esto es, el aire que lo
rodea, y de un proceso infinitamente lento, para garantizar que en cada estado
intermedio el sistema alcance el equilibrio y además, isotérmico. Por estas
razones decimos que el proceso isotérmico es también ideal. Veamos un ejemplo
muy simple.
Si queremos evaporar una cierta cantidad de agua y la ponemos en un recipiente
metálico, hay que calentarla. A la presión de 1 atmósfera, e.g. el nivel
del mar, la temperatura de ebullición es de 100ñC y se mantiene constante durante
toda la ebullición. Por otra parte es sabido que para evaporar 1 g de H20
hay que suministrarle una cantidad de calor igual a 540 calorías y por lo tanto,
si concebimos la evaporación de un gramo de agua a 100ñC como un proceso ideal,
el cambio en la entropía del agua será:
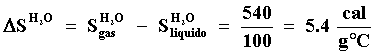
Pero éste no es el único cambio de entropía. El cuerpo a 100ñC que suministró
el calor para hervir el agua y cuya temperatura es de 100ñC, también cambia
su entropía pues como pierde 5.4 cal por cada gramo de agua que se evapora,
ese cambio será:
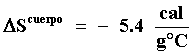
Por lo tanto sumando ambas contribuciones vemos que
Sin embargo, cuando el proceso no es ideal entonces
pero no obstante DSH2O sigue siendo 5.4 cal/gñ C pues la entropía del agua en sus estados inicial (líquido) y final (gas) no depende de la naturaleza del proceso; la entropía es una función de estado. Luego en este caso ya no podemos afirmar algo concreto respecto al cuerpo o los alrededores excepto que el cambio en su entropía debe ser tal que la suma total sea positiva.
Hasta este momento hemos dejado a la imaginación y a la intuición del lector
la conceptualización de los estados de equilibrio y por lo tanto de los procesos
reversibles. Vale la pena tomar unos minutos para precisar ambos. Un estado
de un sistema está definido por ciertos atributos medibles del sistema. Atributos
ya conocidos son la presión p, el volumen V, la temperatura T, la energía U
el campo eléctrico 
, el campo magnético 
,
la polarización 
,
la magnetización 
,
etc. Cuántos atributos es necesario conocer para determinar el estado depende,
como veremos más adelante, de la elección del sistema. Para un fluido simple,
por ejemplo, bastan 2 usualmente elegidos como la presión y la temperatura.
En el caso en que los valores numéricos de estas variables no cambien con el
tiempo, esto es permanezcan constantes, por lo menos durante un intervalo de
tiempo suficientemente grande comparado con la duración de una observación del
sistema, decimos que el estado es uno de equilibrio. Por ello es que un proceso
ideal o reversible debe ser muy lento, para garantizar que en cada estado intermedio
las variables de estado no cambien con el tiempo. Además, para poder invertir
el proceso la fricción debe ser estrictamente igual a cero. Ni una ni la otra
condición ocurren en la práctica.
Volviendo a la interpretación de la ecuación (11) es posible ahora intentar explicar la desigualdad como una contribución de la fricción y otros factores no presentes en los procesos ideales. Aunque esta idea es correcta en principio, su discusión pertenece al dominio de la termodinámica de procesos irreversibles que veremos subsecuentemente en el capítulo V.
De nuestro ejemplo para la evaporación del agua y obviamente su condensación, donde todo el razonamiento es válido cambiando de signo a las respectivas cantidades de calor, vemos que para procesos ideales e isotérmicos, se obtiene la igualdad en la ecuación (11). Esto se debe a que la ganancia (o pérdida) de entropía del sistema se compensa por la pérdida (o ganancia) de entropía de los alrededores (cuerpo, atmósfera, etc.). Este resultado suele escribirse como
entendiendo por universo (ñuna palabra muy desafortunada!)
al conjunto formado por el sistema y aquel (o aquellos) cuerpo (o cuerpos) que
intervienen en el proceso. En el caso en que el proceso no sea ideal,
la ecuación anterior suele escribirse como
 |
(15a) |
sin que este resultado sea extensivo a connotaciones cosmológicas de la palabra
universo. Cuando el proceso es además adiabático, esto es, ocurre en condiciones
totales de aislamiento de manera que no pueda intercambiar ninguna forma de
energía con sus alrededores, entonces
 |
(15b) |
y si más aún, el proceso es reversible o ideal, la entropía es constante. Éste es precisamente el caso de los dos procesos C2C3 y C4C1 del ciclo de Carnot (Fig. 5). El gas pasa de un estado inicial a P2 y volumen V2 a un estado final a presión p3 y volumen V3 pero la entropía en C2 digamos S2 es igual a la entropía en C3; análogamente, S4 = S1. Sin embargo, si los procesos fueran irreversibles S3 >S2 y en la expansión C1C4 del proceso inverso a C4C1 S4> S1.
Generalizando este argumento a la expansión indefinida de un gas, aislado de sus alrededores, cuanto mayor sea la expansión mayor será el incremento de S y obviamente para su punto terminal, S alcanzará un valor máximo. Estos resultados guardan cierta semejanza con el enunciado (2) de Clausius pues en ambos casos aquí discutidos, el universo es el termodinámico y el máximo de la entropía se refiere a procesos adiabáticos y aislados, esto es a situaciones muy bien definidas.
Podemos resumir esta discusión de la manera siguiente: tomamos un sistema para su estudio, lo caracterizamos a través de las variables termodinámicas adecuadas y lo aislamos del medio ambiente que lo rodea. Esto quiere decir que las paredes del recipiente que lo contiene (ño bien su superficie si es un sólido!) son impermeables, esto es, no permiten intercambio de materia para garantizar que la masa permanece constante. Además, esas paredes se cubren de un aislante perfecto para evitar intercambio de calor y por último no se permite que el sistema intercambie energía mecánica, eléctrica, magnética, etc., con el exterior. Si en ese sistema ocurre un proceso cualquiera su entropía no puede disminuir. Esto es, consistentemente con el valor constante de su energía interna U, la entropía alcanza un máximo. Hasta este momento, ésta es la única interpretación, legítima y justa que podemos dar de la desigualdad (11) para sistemas aislados. Además, hay que agregar que la influencia de la fuerza provocada por la aceleración de la gravedad local, en el sitio del experimento, es despreciable o nula. Esto es válido para sistemas de dimensiones pequeñas comparadas con aquellas para las cuales las variaciones de la aceleración de la gravedad no es despreciable. Si exactamente el mismo proceso ocurre para el sistema descrito en las mismas condiciones, excepto que las paredes del recipiente no son aislantes y puede intercambiar calor con sus alrededores, los cuales se supone se encuentran a temperatura constante, entonces la ecuación (11) adopta la interpretación descrita por las ecuaciones (15a,b). Si el proceso es ideal, la entropía del universo formado por el sistema y sus alrededores, se conserva.
De aquí se desprende que cualquier aplicación de la ecuación (II), o sus formas (15 a,b), a sistemas termodinámicos abiertos, esto es, con paredes o superficies permeables a la materia y que permitan el intercambio de masa y/o en presencia de campos externos (en particular el campo gravitatorio ya no despreciable a nivel interplanetario, intragaláctico o cosmológico) requiere forzosamente de hipótesis adicionales que deben establecerse con toda claridad. Por ejemplo, en el caso de la termostática simple, las ecuaciones (11) y (15 a,b) en forma de desigualdades no son enteramente válidas para sistemas abiertos. Eso no implica que no pueda calcularse la entropía de un sistema abierto, lo que implica es que de hacerlo hay que introducir una hipótesis adicional que en este caso se limita a suponer que tanto la energía interna U, el volumen V, la entropía S como otras variables que dependan del tamaño del sistema, sean funciones aditivas. Esto es, la entropía total es la suma de las entropías, etc. Por lógico y simple que esto parezca no deja de ser una hipótesis cuyas consecuencias sólo pueden cuantificarse al comparar los resultados teóricos que de ellas emanen, con los resultados del experimento. Por ejemplo, si en un recipiente mezclamos agua y aceite y lo agitamos veremos que los dos componentes se separan de nuevo para formar dos sistemas homogéneos, pero entre ellos hay una interfase formada por una mezcla de agua y aceite. Esta interfase desempeña un papel muy importante en múltiples problemas de aplicación práctica de la termostática y bajo la hipótesis anterior por ejemplo, el que la energía total del sistema sea la suma de las energías del agua y del aceite, implica que la interfase queda excluida del sistema. Si se le quiere incluir entonces es necesario decir bajo qué hipótesis adicionales, pues no deja de ser un mezcla (emulsión, suspensión, etc.) de los dos componentes puros.
En síntesis, el cálculo de S, U, etc., puede hacerse a expensas de mayor información pero ésta ya es ajena a las ecuaciones (11 ) y (15a,b). Sobra decir que en el caso del universo cosmológico la situación es más delicada pues no sólo los diversos sistemas son abiertos sino que la presencia de la gravitación es ineludible. Volveremos a este punto después.
Si bien es cierto que hemos hecho un esfuerzo relativamente grande en aclarar
el dominio de validez y el significado físico de la ecuación (11), todavía subsiste
la pregunta acerca de la concepción física de lo que es entropía. Esta cuestión
la vamos a tratar aquí desde un punto de vista estrictamente fenomenológico.
Es más, la idea esencial que se desea esgrimir es que el significado físico
de S surge de una manera tan simple y tan espontánea como surge el concepto
de temperatura; ambos son una necesidad inherente a lo que entendemos por un
sistema en termostática y no es necesario recurrir a conceptos moleculares para
interpretar a una y a otra. El aspecto molecular lo dejaremos para otro volumen
de esta serie que versa sobre la teoría molecular de la materia.7
Repasemos entonces el origen del concepto de temperatura. Para eso, imagine el lector que tiene a su disposición un conjunto de cuerpos macroscópicos que arbitrariamente etiquetaremos con las letras A, B, C, D, .... etc. (Fig. 8). Se sobreentiende que estos cuerpos tienen propiedades en grueso, medibles en el laboratorio y cuyo valor es insensible al número de moléculas que contienen. Ésta es la conceptualización más elemental de un sistema macroscópico. Ahora preguntamos si es posible establecer una relación de orden entre dichos cuerpos en base a su grado relativo de calentamiento ordenándolos de los más fríos a los más calientes, o viceversa. Lo más natural es que se recurra al sentido del tacto para realizar la operación con el grave peligro de que si alguno de ellos no está en polos opuestos (hielo, agua hirviendo, un metal al rojo vivo, etc.) nuestro sentido no sea suficientemente preciso para distinguir entre uno y otro.
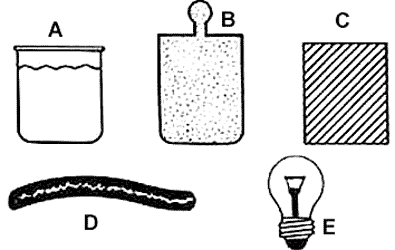
Figura 8. Sistemas microscópicos arbitrarios como pueden ser un líquido A, un
gas B, un trozo de metal C, un trozo de hule D, un bulbo de luz E, etc.
ñCuántas veces apreciamos lo subjetivo de esta medición al discutir con otra persona si un objeto dado se "siente más caliente o más frío" que otro! Así pues, tenemos que recurrir a un método más preciso el cual está basado en un hecho común y corriente. Si tomamos dos de estos cuerpos y los ponemos en contacto entre sí, llega un momento en que uno estará igual de caliente (o frío) que el otro, esto es, su grado relativo de calentamiento es el mismo. Si un tercero del conjunto inicial resulta estar igualmente frío o caliente que cualquiera de los primeros dos, estará también igualmente frío o caliente con el tercero. En un lenguaje más técnico decimos que los tres están en "equilibrio térmico " entre sí. Esta proposición elevada a la categoría de axioma se conoce como la ley cero de la termostática: "Si de tres cuerpos A,B y C, A está en equilibrio térmico con B e independientemente A está en equilibrio térmico con C, entonces B y C están en equilibrio térmico entre sí."
Este axioma que constituye en esencia la racionalización de las ideas subyacentes
a las mediciones de temperatura que datan del siglo XVIII, no fue
apreciado y planteado sino hasta principios de este siglo, después de que las
dos primeras leyes ya habían sido enunciadas. De ahí que se le haya bautizado
como ley cero. Pero volvamos a nuestro experimento: una vez que dos o más cuerpos
están en equilibrio térmico entre sí debemos buscar qué propiedad tienen en
común y establecer un método para medirla. Esa propiedad, que debe ser inherente
al sistema, se conoce como temperatura. De ahí que la ley cero puede también
enunciarse diciendo que dos o más cuerpos están en equilibrio térmico entre
sí, cuando tienen la misma temperatura. El mercurio de un termómetro de bulbo
alcanza la temperatura de 36.8ñC cuando el mercurio metálico está en equilibrio
térmico con la temperatura del cuerpo humano.
Una vez identificada la existencia de la propiedad, sólo hay que adoptar una serie de reglas arbitrarias para medirla. Ese conjunto de reglas basadas en la adopción de un patrón de comparación o un estado estándar se conoce como "termometría". Así pues, como las "reglas sirven para medir longitudes, los relojes, tiempo, etc., basados en ciertas unidades adoptadas empírica, pero convenientemente, los termómetros miden temperaturas (Fig. 9). Y si disponemos de uno suficientemente sensible somos capaces de responder a la pregunta planteada, es decir, si A está más o menos caliente que B, éste que C, etc. La cuestión original v.g. lograr ordenar la secuencia de cuerpos en base a su grado relativo de calentamiento surge como una necesidad inherente a las propiedades de estos cuerpos y su respuesta depende de identificar la variable apropiada, en este caso la temperatura.
La tesis que vamos a esgrimir aquí, por cierto un tanto novedosa y poco discutida en la bibliografía establecida, es que la entropía, como la temperatura, surge de una necesidad misma planteada por la definición de lo que es un sistema termodinámico. Empecemos pues por definir un sistema. En la literatura convencional se dice que un sistema es una "porción del universo físico que se aísla para su estudio". En la práctica es algo más. Si nosotros queremos "aislar esa porción" sólo lo podemos hacer a través de las restricciones que nosotros le imponemos para su aislamiento. En efecto, queremos un sistema finito, manejable, perceptible, etc., luego sus "dimensiones" deben quedar especificadas, ya sea porque su volumen, área o longitud queden determinadas por el recipiente que lo contiene, si ese es el caso, o por las superficies que limitan al volumen (si es un sólido tridimensional), o por la curva que encierre una área (si es bidimensional como una película delgada). Así pues, el sistema empieza por tener restricciones geométricas. Estas restricciones tienen asociadas un parámetro medible, el volumen (V), el área (A) o la longitud (L).
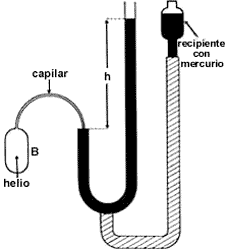
Figura 9. Un termómetro de gas a volumen constante. El bulbo B se llena con un gas, de preferencia helio, y se pone en contacto con agua en su punto triple. La altura de la columna de mercurio ht permite calcular la presión del gas a la temperatura del agua en dicho punto. En seguida, el bulbo se pone en contacto con el cuerpo cuya temperatura se desea medir. La nueva altura de la columna hc permite calcular la resión del gas. La temperatura T del cuerpo se obtiene de la fórmula
Otro tipo de restricción que podemos imponer al sistema es, justamente, de carácter térmico: si queremos que esté en equilibrio térmico con sus alrededores hay que permitir que esté en contacto térmico con él a través de paredes conductoras (metálicas en general) y con ello su temperatura T será la misma que la de sus alrededores. O bien, podemos rodearlo de un material aislante y con ello garantizar que no haya transferencia de calor entre él y sus alrededores. Si en un caso u otro las paredes son permeables o impermeables al paso de materia, tendremos restricciones de carácter químico y de ellas dependerá si el sistema es abierto o cerrado y, en el primer caso, en qué medida. Finalmente podemos imponer restricciones mecánicas permitiendo que, si está en contacto con la atmósfera, su presión sea igual a la atmosférica o fijando el valor de esa presión por medios mecánicos, un pistón si es un fluido, una prensa si es un sólido, etc. Una vez que hemos definido nosotros, el observador, el sistema que queremos estudiar, hemos consciente o inconscientemente determinado el número de restricciones a que está sometido el sistema y cada una está caracterizada por el valor numérico asignado a un atributo medible. El número de restricciones determina el número de grados de libertad y, automáticamente, el número de variables independientes necesarias para describir los estados del sistema en esas condiciones. Estas consideraciones responden a una pregunta formulada con anterioridad en conexión con el número de variables requeridas para especificar los estados de un sistema. Un gas encerrado en un recipiente con paredes conductoras sólo tiene dos restricciones, la térmica y la geométrica, luego sólo son necesarias dos variables independientes que podemos escoger, al gusto, entre p. V, T u otras.
Si el gas es paramagnético y queremos especificar su magnetización es necesario introducir otra restricción especificando el valor de la magnetización, o el del campo magnético externo a que está sujeto. Hay tres restricciones, por lo tanto hay tres grados de libertad y se requieren tres variables independientes. Si el gas está formado además por una mezcla de dos gases inertes y es cerrado, esto es si la masa total es constaante, hay que especificar el número de moles, o la cantidad de materia de cada gas y por lo tanto se requieren dos variables adicionales, pues la mezcla gaseosa, paramagnética e inerte, tiene cinco restricciones; y así sucesivamente.
El lector puede ahora concebir los sistemas que le vengan a la mente en este lenguaje y le será fácil identificar el número de variables independientes. Nótese que el problema de elegir a esas variables es diferente pues en general, como ilustramos en el caso del gas, hay un número de las elegibles mayor que el requerido y la elección se hace estrictamente con base en la convivencia.
Una vez definido lo que es un sistema y de insistir en que hay una correspondencia uno a uno entre el número de restricciones, de grados de libertad y de variables independientes llegamos al punto crucial de nuestra discusión. Sí consideramos a un sistema aislado y cerrado (y suponemos que la acción del campo gravitacional es despreciable o nula) siempre es posible remover una restricción sin afectar el estado del sistema. Más aún, en el instante en que se remueve dicha restricción se induce un proceso durante el cual el sistema realiza trabajo útil sobre sus alrededores. Al llegar a su estado final, éste se caracteriza por las restricciones restantes, que suman una menos que en el estado inicial. Así pues, tenemos un estado de equilibrio menos restringido que el estado inicial. Vamos a ilustrar esta secuencia con dos ejemplos de índole diferente. En el primero pensemos en un recipiente: de paredes rígidas impermeables y aislantes (ver Fig. 10) que contiene una pared montada sobre ruedas u otro dispositivo que permita su deslizamiento sobre un riel. La pared se encuentra inicialmente en un punto tal que divide al recipiente en dos partes cada una conteniendo a un gas (si son iguales o diferentes es irrelevante), de manera que el gas que ocupa la porción de volumen V1 tenga una presión p1 mayor que la del gas que ocupa el volumen V2 y que designaremos por p2. En este sistema hay tres restricciones, a saber, el volumen total es constante, la energía total es constante (aislamiento) y las presiones de los dos gases son diferentes p1 > p2 . El sistema tiene tres grados de libertad y por lo tanto hay tres variables independientes que pueden escogerse a voluntad de la lista p1, p2, V1, V2, V, U, T1,T
2, etc.
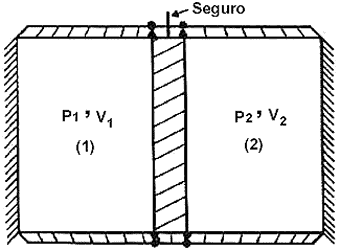
Figura 10. Dos gases encerrados en un recipiente aislado están separados
por una partición tal que p1 > p2. Al remover el seguro
la partición oscila hasta alcanzar un estado de equilibrio que corresponde a
p1 = p2.
Si ahora removemos el seguro que mantiene a la partición, ésta se moverá al principio hacia la derecha, oscilará por un rato y finalmente se detendrá en una posición que corresponderá al estado en que haya equilibrio mecánico, esto es, cuando p1 = p2 (ñtal como en el émbolo de una bomba de mano para inflar llantas!). Véase que la acción de remover el seguro no afecta el estado del sistema e induce un proceso. Al final de este proceso el sistema alcanza otro estado de equilibrio en el cual se ha perdido la restricción p1 > p2 y sólo quedan dos restricciones disponibles, V= constante y U = constante. El sistema tiene ahora un grado de libertad menos que en su estado inicial. Además de haber atado una cuerda a un cuerpo dado o a la manivela de un generador, podríamos haber utilizado la diferencia inicial de presiones a través del movimiento de la pared para elevar dicho cuerpo a una altura determinada, o a través de la rotación de la manivela del generador producir una corriente eléctrica. Esto es, en el proceso inducido (ñno espontáneo!) se genera una cierta cantidad de trabajo útil. Es más, si quisiéramos restaurar la restricción inicial o regresar la partición a su posición original, forzosamente tendríamos que realizar trabajo sobre el sistema (ñcomprimir un gas!).
En el segundo ejemplo, que es de naturaleza completamente diferente al anterior,
supongamos que en un cilindro de vidrio pyrex, cuyas paredes estén bien forradas
con asbesto, tenemos inicialmente una cierta cantidad de tetróxido de nitrógeno
N2O4. Éste se encuentra a una presión menor que una atmósfera
y mezclado con una cantidad pequeña de NO2, de manera que no exista
una reacción química entre ellos. La presión se controla mediante un pistón
fijo como el que se ilustra en la figura. El sistema tiene entonces cuatro restricciones,
una mecánica que mantiene el volumen V = const., la energía U = const. y las
dos concentraciones de los óxidos de nitrógeno que podemos llamar C1
y C2 respectivamente. Hay pues cuatro variables independientes que
pueden escogerse arbitrariamente entre p, V, T, U, C1, C2,
etc. Si ahora, sin perturbar la condición de aislamiento agregamos un catalizador
al sistema, se establece el equilibrio químico de acuerdo con la reacción
2 NO2
y por consiguiente en el estado final, también de equilibrio, las concentraciones
de ambos gases ya no son independientes pues por cada gramo mol que haya
de N2O4 hay 2 gramos mol de NO2. El sistema
tiene sólo tres restricciones y por lo tanto sólo requiere tres variables independientes.
Hay, sin embargo, una sola diferencia aparente con el ejemplo anterior pues
el trabajo realizado por el sistema no es tan palpable como en la remoción del
seguro de la pared separadora entre los dos gases. La naturaleza de la restricción
removida es mucho más sutil en este caso pues la presencia del catalizador lo
que hace es "activar" la energía de las moléculas de N2O4
para que al chocar entre sí, aquellas que sean suficientemente energéticas transformen
su estructura electrónica y se conviertan, por lo menos una de ellas, en dos
moléculas de NO2. La energía liberada en este proceso y que se manifiesta
en calor de la reacción, es desde luego de naturaleza química y, en principio,
podría aprovecharse en trabajo útil. El lector puede apreciar también si quisiéramos
restaurar al sistema a su estado inicial, habría que realizar trabajo externo,
requerido para desplazar el equilibrio hacia la izquierda según
la reacción
hasta restituir la concentración inicial de N2O4.
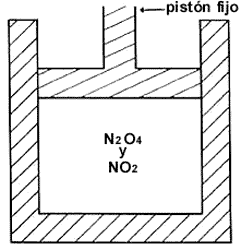
Figura 11. La presencia de un catalizador en la mezcla de
N2O4 y NO2 activa la reacción N2O4 
2 NO2 y libera al sistema de una restricción.
Aunque podríamos continuar con una larga lista de ejemplos similares,, estos dos bastan para ilustrar nuestro propósito, a saber, en todo sistema aislado es posible, mediante la remoción de una restricción, inducir un proceso y en ese proceso inevitablemente el sistema realiza trabajo externo. Con este arsenal de ideas podemos ahora dar una interpretación clara y concisa sobre el papel que juega la entropía en clasificar a los sistemas termodinámicos en función de una característica inherente a su construcción. Para mayor claridad, plantearemos ahora una cuestión de manera completamente similar a como lo hicimos con el concepto de temperatura. De toda la exposición anterior, se desprende que una faceta ineludible en la caracterización de un sistema la constituye el número de restricciones que se le imponen en su construcción o definición. Piense ahora el lector de nuevo en el conjunto de cuerpos o sistemas macroscópicos que etiquetamos con las letras A, B, C, D... al empezar nuestra discusión sobre el concepto de temperatura ( Figura 8).
Ahora bien, en vez de establecer una relación de orden entre ellos en base a su mayor o menor grado de calentamiento, pensemos en si es posible o no establecer entre ellos una relación en base a lo que llamaremos su "grado de restricción". Nótese que el número de restricciones no es suficiente para hacerlo, pues hay muchos de este conjunto que poseerán, digamos dos restricciones, otros tres, otros cuatro, etc.
Esto es tan burdo y tan inútil como haber pensado en un grado de calentamiento etiquetado en base a los números enteros positivos. Así como el grado de calentamiento es la base para establecer el concepto de equilibrio térmico y de ahí extraer la existencia de un atributo inherente a cada sistema que después bautizamos como su temperatura, la pregunta aquí es similar. ¿Existe un atributo inherente a los sistemas macroscópicos capaz de medirse por métodos rigurosos y aplicables a todo sistema, susceptible de cuantificar su grado de restricción? O en términos diferentes, así como cuando dos o más cuerpos están en equilibrio térmico entre sí afirmamos que tienen una propiedad en común que se define como temperatura, ¿es posible establecer un método experimental irrefutable que nos permita cuantificar el grado de restricción de un sistema termodinámico? Nótese claramente que aquí en cierto modo partimos de la hipótesis de que dicho grado de restricción es un atributo medible y queremos asignarle un número que lo caracterice como hace la termometría con la temperatura. Así pues, nuestro punto de partida es el siguiente:
1) Suponemos que es posible cuantificar el grado de restricción de un sistema. A este lo llamaremos C.
2) Si C existe, entonces por construcción debe ser un atributo del sistema ya que las restricciones impuestas se caracterizan por tales atributos: p, V, ... T, etc., y C sólo puede ser función de ellos.
3) En un sistema aislado, C sólo puede depender de los atributos asociados a variables extensivas, esto es a las variables como U, V, M (la masa), etc., que dependen del tamaño o extensión del sistema. En efecto si queremos imponer restricciones sobre variables intensivas como T, p, etc., no podemos aislar al sistema de sus alrededores, pues para fijar T se requiere tenerlo en contacto con otro cuerpo a dicha temperatura, para fijar p hay que mantenerlo en contacto mecánico con una atmósfera a dicha presión a través de un émbolo o pistón movible, etc.
4) Si removemos una restricción de un sistema aislado, lo cual es posible sin alterar al sistema, se induce un proceso a otro estado menos restringido durante el cual el sistema realiza trabajo.
A partir de las cuatro premisas, se busca ahora una forma de cuantificar C como una función de las variables extensivas, C = C (U, V, ... ). A este efecto observemos primero que si quitamos una restricción en un sistema aislado general el proceso inducido correspondiente es uno irreversible y como tal, difícil de utilizar para realizar una medición de alguna cantidad que varíe en su transcurso, aunque el trabajo realizado surge como un candidato razonable. Pero pensemos en el estado final de equilibrio menos restringido al que llega el sistema después de la remoción de la restricción y en el proceso que tendríamos que realizar para restaurarla. Este proceso, lo podríamos llevar a cabo cuasiestática y reversiblemente tomando especial cuidado de no alterar las condiciones en que ocurrió el proceso original para garantizar que en cada etapa infinitesimal del proceso inverso al original, el cambio en el grado de restricción, llamémosle dC, sea el mismo en ambos. Con esta idea en mente es posible mostrar8que independientemente de la naturaleza del sistema que se emplee para realizar la operación
 |
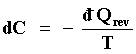(16) |
En otras palabras, la variación en el grado de restricción para cualquier sistema
en una porción infinitesimal de una trayectoria, que corresponde a un proceso
reversible inverso al proceso que se realiza al remover una restricción, es
igual a menos el calor reversible que el sistema intercambia con un cuerpo con
el que debe estar en contacto y que se encuentra a una temperatura T, dividido
entre la temperatura de dicho cuerpo. Más aún, como el calor es una propiedad
extensiva, C resulta ser, como se requiere, una cantidad extensiva. El cambio
total en C entre el estado inicial y el final, ambos estados de equilibrio pero
el segundo ahora con una restricción más que el primero, se obtiene simplemente
sumando todas las contribuciones infinitesimales indicadas por la ecuación (16).9
Estos resultados constituyen la conclusión medular de esta discusión. En
efecto, si tomamos a un sistema aislado es posible inducir uno o varios procesos
removiendo una o varias restricciones de manera que el grado de restricción
disminuya continuamente. Desde este punto de vista, a medida que un sistema
va perdiendo sus restricciones, el sistema se va "desorganizando" cada vez más.
Como esta desorganización ocurre cuando el sistema se mantiene aislado de sus
alrededores, y por consiguiente su energía interna es constante, los cambios
inducidos a energía constante siempre ocurren en una dirección en la cual la
desorganización del sistema aumenta. Recíprocamente, si a energía constante
el grado de restricción aumenta, la organización también aumenta. Así pues,
en sistemas aislados, los procesos inducidos ocurren al reducir el número de
restricciones y por consiguiente como Ci > Cf donde i y f representan los
estados inicial y final respectivamente.
| DC
< 0 |
(17) |
Si ahora comparamos esta desigualdad con la expresada por la ecuación (11)
que constituye un corolario de la segunda ley de la termodinámica, también válido
para sistemas aislados, ambos son iguales entre sí al identificar
| S = ¾
C |
(18) |
Esto establece de una manera clara y concisa el significado de entropía: es una medida de la "falta de grado de restricción" en un sistema o si se quiere, en términos más pedestres, es una medida de la desorganización. Ciertamente, la cantidad ¾ S = C hubiera sido más satisfactoria desde el punto de vista físico, pues es más en la organización que en la falta de ella, pero el origen de la función S, como vimos anteriormente, le impuso el signo positivo.
Para ilustrar el significado de las ecuaciones (16) y (17) tomemos un ejemplo de la vida cotidiana: el cajón de un archivo en el cual la correspondencia, o documentación archivada alfabéticamente y separada por separadores etiquetados desde la A hasta la Z. Esta disposición corresponde a la de un sistema en su grado máximo de organización, en este caso por medio de veintisiete restricciones. La remoción de un separador "induce" un proceso mediante el cual, en el transcurso del tiempo ocurre que la correspondencia entre los dos separadores próximos más cercanos empieza a entremezclarse hasta alcanzar un "estado final" en el cual sea imposible saber a cuál de las dos letras afectadas pertenece. Este estado final es uno con una restricción menos y por lo tanto menos organizado.
De acuerdo con las fórmulas anteriores C disminuyó pero S aumentó. La entropía es pues mayor en el estado menos organizado de manera que si continuamos removiendo separadores, C continuará disminuyendo y S continuará aumentando.
Volviendo al caso de los sistemas termodinámicos podemos también afirmar que un sistema está mejor organizado cuanto mayor es el número de restricciones sobre él impuestas. Piense el lector, por analogía con el archivero, en un conjunto arbitrario de gases, todos diferentes y separados entre sí por particiones impermeables. Al remover restricciones, particiones en el caso de los gases, se inducen procesos en los cuales el número de restricciones disminuye y la entropía aumenta. Al estar los n gases mezclados entre sí la desorganización es máxima así como su entropía. En sistemas aislados y cerrados, la entropía es una medida del grado de desorganización, entendida ésta como la carencia de restricciones. Y en este sentido la entropía, como dijimos al enunciar esta larga discusión, surge como una necesidad de la definición misma de lo que es un sistema.
Para terminar con este capítulo falta sólo esbozar la idea de como puede medirse
la entropía. Esto es lo que finalmente nos permitirá establecer la relación
de orden buscada entre el conjunto de cuerpos A, B, ... en términos de su "grado
de restricción". Como lo indica la ecuación (15) que define el cambio en el
grado de restricción para un proceso infinitesimal, lo que se requiere medir
es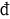 
Qrev y T. Con respecto
a la temperatura no hay problema, pues disponemos de termómetros para medirla.
En cuanto al calor transferido entre el sistema y el cuerpo a la temperatura
T tenemos dos métodos para medirlo, uno directo recurriendo a la calorimetría
y otro indirecto, que es usual y que hace uso de la definición de Q dada por
la ecuación (3)
En efecto, dU la sabemos medir según la ecuación (1) y el trabajo mecánico es también medible específicamente en un proceso reversible. Así pues las dos cantidades involucradas con la definición de C son accesibles al observador y por lo tanto C es calculable. En el caso más difícil hay que sumar todas las contribuciones infinitesimales que: componen al proceso en cuestión y de ahí obtener DC.10 Con ello concluimos que los cuerpos A, B, C, D,... quedarán ordenados de manera tal que los menos "organizados" tendrán una mayor entropía.
NOTAS
7 Leopoldo García Colín, Teoría cinética de la materia (vol. en preparación).
8 El lector interesado en los detalles de la demostración puede consultar: L. García-Colín. Introducción a la termodinámica clásica, Editorial Trillas, tercera edición, México, D.F.,1986
9 Para el lector familiarizado
con el concepto de integral.
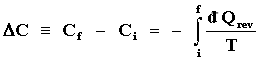
10 En términos de la nota al pie de la pagina (73), DC se obtiene al llevar a cabo la integral de línea correspondiente.
