XX. LA MECÁNICA CUÁNTICA
SI ACEPTAMOS las ideas de Louis de Broglie y a cada partícula
le asociamos una onda con l = h/p,
nada hay más natural que aplicarlas también a los electrones dentro del átomo,
digamos a una órbita circular. Nos hallamos entonces frente a un dilema, a menos
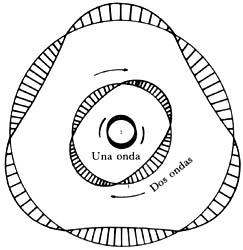
que un número entero de longitudes de onda cubra toda la circunferencia. De
otra forma, no podríamos asociar unívocamente un valor definido de la onda a
cada punto. Ello implica que sólo un conjunto discreto de longitudes de onda,
y de ahí sólo valores discretos del ímpetu, sean posibles. Nos acercamos así
a las órbitas de Bohr, necesarias para explicar el espectro discreto del átomo
de hidrógeno.
Ideas como la expuesta en el párrafo anterior llevaron a Erwin Schrödinger, físico austriaco, a proponer la mecánica ondulatoria. Cuando se enteró —al leer un trabajo de Einstein— de las ideas de Louis de Broglie, se le ocurrió tomarlas en cuenta para enfocar el modelo atómico de Bohr desde otro ángulo. Al imaginar que las ondas fueran estacionarias, podríamos pensar que representan una carga sin aceleración que, por lo tanto, no radia. Todo ello condujo a Schrödinger a su ecuación, que sería la ecuación básica de la mecánica cuántica no-relativista.
Antes de Schrödinger y de De Broglie nos enfrentábamos a la dualidad partícula-onda de la luz; después de ellos, esta dualidad era omnipresente en el mundo microscópico. Para entender algunos experimentos —como el fotoeléctrico o el de Compton en el caso de la luz—, debíamos pensar en partículas; otras veces —como en aquellas situaciones donde hay interferencia—, hablaríamos de una onda. A veces pensamos en una partícula y su trayectoria, lo que implica suponer que la posición y el ímpetu lineal del sistema se pueden conocer con tanta precisión como deseemos; otras veces hablamos de una onda, con su longitud de onda y su frecuencia bien definidas, y que puede difractarse o sufrir interferencia. Todo ello no ocurre cuando se observa el movimiento de los cuerpos grandes, como proyectiles, trenes o planetas. Algo debe haber en el mundo de las partículas pequeñas que se nos ha escapado.
Otro maestro de los experimentos pensados encontró la pieza faltante. En 1927, un joven físico alemán, W. Heisenberg, que por aquel entonces tenía apenas 26 años, formuló el principio de incertidumbre, según el cual es imposible determinar al mismo tiempo la posición y el ímpetu de cualquier cuerpo. Su razonamiento sigue esta línea: Al hacer una partícula más y más pequeña, la hacemos más y más sensible a perturbaciones. Cuando observamos una partícula, debemos verla en alguna forma y para ello es necesario iluminarla con luz de frecuencia apropiada. Mientras más pequeña sea la partícula requerimos luz de longitud de onda menor y, por lo tanto, de mayor frecuencia. Lo anterior implica usar fotones cada vez más energéticos, que deben rebotar en la partícula para luego llegar a nuestro ojo, al microscopio o a cualquier otro detector que empleemos. Por tanto, la velocidad de la partícula sufre cambios cada vez mayores, pues la colisión con los fotones la altera más. A medida que deseemos determinar mejor la posición, la velocidad de la partícula será más imprecisa. De hecho, según el principio de Heisenberg, el producto de los errores con que podemos medir posición e ímpetu de una partícula tiene un mínimo, que es inherente a la naturaleza. Este valor mínimo está dado por la constante de Planck h.
El principio de Heisenberg destruye el concepto de partícula (y, desde luego, el de órbita) y por lo tanto resuelve la paradoja partícula-onda. Antes de Heisenberg teníamos una situación que recuerda a aquella que existía antes de Einstein y su teoría de la relatividad. Nunca pensaron los físicos de finales del siglo XIX en cuestionar lo absoluto del tiempo, ni imaginaron que la simultaneidad de dos eventos fuera relativa al observador. En la misma forma que Einstein sujetó a una dura crítica los conceptos sobre el tiempo que se creían válidos, Heisenberg destazó las ideas en boga sobre partículas y ondas. Su principio destruyó las ideas clásicas de partículas y de onda, como antes lo había hecho la teoría de la relatividad de Einstein con el tiempo absoluto. Los conceptos de ondas y partículas son habituales en nuestro mundo cotidiano —porque en él vemos cuerpos grandes y lentos— pero en el mundo microscópico se reducen a una mera forma de hablar y ya no son aplicables a los procesos atómicos o nucleares.
Incluso antes de formular su fundamental principio, Heisenberg había encontrado un camino para entender el modelo de Bohr, camino que a primera vista es diferente al marcado por Schrödinger. Al usar únicamente cantidades observables, Heisenberg fundó la mecánica de matrices; no nos detendremos en ella pues pronto se demostró que sus conclusiones eran idénticas a las que pueden obtenerse de la ecuación de Schrödinger. La mecánica de matrices de Heisenberg y la mecánica ondulatoria de Schrödinger son, pues, dos maneras equivalentes de formular lo que hoy llamamos la mecánica cuántica.
En la mecánica cuántica no caben ya las trayectorias que siguen las partículas clásicas. Se les ha cambiado por las soluciones de la ecuación de Schrödinger, que por comodidad seguiremos llamando ondas. ¿Cómo es que estas ondas de Schrödinger reemplazan al viejo concepto de órbita? La respuesta a esta crucial pregunta la dio Max Born, poco después de la invención de la mecánica cuántica. Según Born, el cuadrado del valor absoluto de la solución y de la ecuación de Schrödinger da la probabilidad de encontrar a la partícula. En aquellas regiones del espacio en que y sea nula, es imposible hallar a la partícula; donde la amplitud de y no es cero, sabemos que es probable encontrarla, aunque no con certeza absoluta. El principio de incertidumbre, que está incluido en la ecuación de Schrödinger, ha destruido el determinismo clásico. En otros términos, la mecánica cuántica es una teoría probabilística, donde la forma de y en el espacio tiene consecuencias importantes.