VIII. NIELS BOHR Y LA FISIÓN NUCLEAR

MARCOS MOSHINSKY

DURANTE los primeros veinticinco años de su vida científica, entre 1910 y 1935, Niels Bohr se concentró en comprender tanto la estructura electrónica de los átomos como la nueva mecánica que se requería para este propósito. Pero, desde su encuentro con Rutherford en 1912, nunca abandonó el interés por el misterioso núcleo alrededor del cual se movían los electrones.

De aquí a partir del descubrimiento del neutrón por Chadwick, en 1932, Bohr dedicó cada vez más atención a la posibilidad de comprender la estructura nuclear en una forma tan completa como antes lo había logrado para la atómica.

Una de sus primeras contribuciones en este campo fue "Captura neutrónica y estructura nuclear"¹ publicada en la revista Nature de febrero de 1936, donde estableció la idea de que las reacciones nucleares tienen lugar en dos pasos: a) La formación de un núcleo compuesto por los dos fragmentos que se ponen en contacto, en donde rápidamente la energía aportada se reparte entre todos los nucleones, y b) La desintegración del núcleo compuesto a lo largo de diversos canales como lo que se indica en la reacción del isótopo 12 del carbón bombardeado por neutrones y que lleva primero al núcleo compuesto ₆C¹³ en un estado excitado,

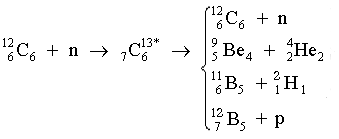(1)

donde los subíndices a la izquierda y derecha del elemento indican respectivamente el número de neutrones y protones. Las probabilidades de desintegración de los diferentes productos que aparecen a la derecha en la fórmula (1), son independientes del proceso que llevó a la formulación del núcleo compuesto, esto es, serían las mismas si se hubiera formado el ₆C¹³, con igual energía de excitación, por ejemplo a través de la reacción de ₄ Be⁹ bombardeado con partículas a.

La idea de Bohr fue fundamental para explicar muchas características de las reacciones nucleares y en particular la presencia de resonancias, como ha sido tratada por Arturo Menchaca. En esta contribución quisiera analizar cómo Bohr implementó esas ideas en el proceso fundamental de la fisión nuclear combinándolas con la analogía del núcleo a una gota de líquido cargada.

Pero antes de entrar a la parte más técnica del análisis quisiera hacer un poco de historia sobre cómo fue descubierto el proceso de fisión nuclear y la excitación que provocó en los físicos y que luego se extendió a la humanidad toda por el impacto de ese descubrimiento.

La historia empieza en 1934 cuando Fermi, enterado de los experimentos de Joliot y Curie para producir radiactividad artificial mediante el bombardeo de partículas cargadas, decidió tratar de inducirla con neutrones. Tuvo gran éxito en su objetivo al estudiar sistemáticamente los elementos de la tabla periódica, notando en el proceso que si la energía de los neutrones se reducía por choques con protones en parafina o en agua, la radiactividad inducida aumentaba grandemente. Al llegar al uranio, resultó que uno de los isótopos radiactivos producidos no pudo identificarse entre los conocidos en esa región de la tabla periódica y se llegó inclusive a pensarse que podría ser un nuevo elemento "transuránico".

El problema del uranio bombardeado con neutrones fue reexaminado: en 1938 por Otto Hahn y Lise Meitner, quienes encontraron de nuevo el misterioso elemento radiactivo de Fermi, así como muchos otros que no podían ser identificados con los cercanos al uranio en la tabla periódica. Las circunstancias políticas en 1938, cuando las fuerzas de Hitler ocuparon Austria, obligaron a Lise Meitner, que era judía austriaca, a abandonar Alemania. Hahn continuó sus experimentos con Strassmann para producir los misteriosos elementos transuránicos y finalmente logró que uno de ellos se precipitara con bario y vio luego que ningún procedimiento químico le permitía separar al "transuránico" radiactivo del bario mismo.

La conclusión era que en alguna forma un isótopo radiactivo de bario se producía al ser bombardeado el uranio con neutrones, lo cual parecía absurdo desde el punto de vista de la física nuclear de la época en que las reacciones con neutrones sólo habían llevado del núcleo bombardeado a núcleos vecinos en la tabla periódica de los elementos. Hahn escribió a Lise Meitner en Estocolmo sobre la paradoja que había encontrado y ésta, con su sobrino Otto Frisch, pronto llegó a la conclusión que posiblemente el uranio se había fisionado y uno de sus fragmentos era el bario. De inmediato Frisch regresó a Copenhague, donde entonces trabajaba, e informó a Bohr que estaba por salir a Estados Unidos para una estancia de varios meses. La reacción de Bohr fue: "Pero qué tontos hemos sido. Esto es maravilloso y justo como debe ser" y sugirió a Frisch y Meitner que inmediatamente escribieran una nota sobre el asunto.

Al llegar a Estados Unidos en enero de 1939, Bohr comunicó la noticia de la fisión del uranio con neutrones a los físicos norteamericanos que de inmediato lo comprobaron mediante diversos tipos de experimentos. En particular, Fermi, ya refugiado en Estados Unidos tras abandonar la Italia fascista, los continuó con entusiasmo.

Bohr decidió aplicar su modelo de la gota de líquido a la fisión nuclear y por cálculos realizados a bordo del barco que lo llevaba a Estados Unidos y continuados en Princeton donde permaneció varios meses en 1939, estableció para empezar que era el isótopo 235 del uranio el que fisionaba con neutrones lentos y luego desarrolló con Wheeler el trabajo "Mecanismo de la fisión nuclear" enviado al "Physical Review" a fines de junio de 1939, y publicado el primero de septiembre, al iniciarse la segunda Guerra Mundial. Poco se imaginaba Bohr que ese trabajo, además de afectar el curso de la física nuclear iba también a influir en la guerra y en la política futura del mundo.

Después de esta introducción quisiera dar brevemente algunos detalles sobre el modelo de Bohr sobre la fisión nuclear.

La interacción fuerte y de corto alcance entre los nucleones en el núcleo sugirió a Bohr que este último tendría más analogía con una gota de líquido cargada (ya que los protones tienen carga) que con un gas encerrado en una esfera. En efecto, para una gota de líquido, la excitación provocada en una de sus partes rápidamente se comunica al resto de la gota por el contacto directo entre las moléculas de la misma y su fuerte interacción, cosa que no sucedería con un gas. De allí que también la gota pierda rápidamente memoria del proceso que la excitó y sólo se ve afectada por la energía que se le proporcionó en ese proceso, lo que sucede también en el caso nuclear, como se indicó en el análisis de la fórmula (1).

Si tenemos una gota de líquido cargada, el equilibrio de la misma se debe esencialmente a la lucha entre dos fuerzas, la repulsión electrostática, que tratará de separar los constituyentes de la gota lo más posible, y la tensión superficial, que resiste toda deformación de la superficie que aumente el área de la misma.

La primera consideración que necesitamos hacer se refiere a la masa de los núcleos. Debido a que los electrones tienen una masa 1,837 veces menor que la de los protones, esta masa es prácticamente la del átomo, y puede medirse a través de alguno de los múltiples métodos de determinar la masa atómica. Pero es importante tener la fórmula semiempírica que nos permita, a través de la relación de Einstein E = mc² entre masa y energía, determinar la masa aún para aquellos núcleos inestables en que ésta no puede ser medida experimentalmente.

Vamos a dar la masa en unidades de energía. El núcleo está caracterizado por A nucleones de los cuales N son neutrones y Z son protones, N + Z = A. La masa entonces toma la forma:

M(A,Z)c² = Nmnc² + Zmpc² - uvA + ur(N - Z)²A-1 + ucZ²A-1/3 + usA2/3 + d

(2)

donde c es la velocidad de la luz.

La masa proviene en primer lugar de la masa de los neutrones y de los protones, pero tenemos que considerar que esos neutrones y protones forman el núcleo por un proceso similar al de la condensación de las moléculas del vapor de agua cuando forman una gota de líquido. Ahora, la condensación libera calor en el caso de las moléculas, y lo mismo sucederá en el caso nuclear. Como esa energía no se da al sistema, sino que éste la da al medio, tiene que volverse negativa y es proporcional a A. La constante de proporcionalidad es uv = 14 MeV donde 1MeV = 1.6 x 10^-6 ergs. Viene después lo que podríamos llamar la energía de simetría proveniente del hecho que los núcleos de igual A (isóbaros), son más estables mientras más cercano esté entre sí el número de protones y neutrones. Más estables significa de menor energía y, por lo tanto, de menor masa, y esto se traduce en el hecho que halla un término proporcional a A^-1 (N ¾ Z)², como una teoría más detallada puede mostrarlo. Viene posteriormente la fuerza electrostática; para una esfera uniformemente cargada de carga Ze y radio R = r₀A^1/3 (se supone que la densidad de la materia nuclear se mantiene aproximadamente constante, y por lo tanto el radio del núcleo es proporcional a A1/3), su contribución a la energía del núcleo es:

(3/5)R-1 Z(Z ¾ l)e² = 4ucA-1/3Z² , donde uc=0.146 Mev.

(3)

El penúltimo término de (1) proviene del hecho que al "condensar" los nucleones, obtenemos menos energía de los nucleones que quedaron en la superficie, que de aquellos que quedaron en el interior del núcleo. Es necesario corregir entonces el término negativo ¾ u_vA, por un efecto superficial que será proporcional al área y, por lo tanto a A^2/3. El coeficiente de proporcionalidad de ese término superficial es u_s = 13 MeV. Finalmente, del hecho que los nucleones tienen spin, y del principio de exclusión de Pauli, se puede demostrar que los núcleos son particularmente estables si contienen un número par de protones Y neutrones, es decir, si N y Z son pares, en cambio son particularmente inestables si N y Z son nones. Esto se refleja en el término d de la fórmula (1) que es igual a:

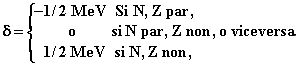(4)

La fórmula (1), conocida con el nombre de fórmula semiempírica de Weizacker² por el nombre del físico que la propuso originalmente, contiene una gran cantidad de información de interés. Consideremos, por ejemplo, la diferencia de energía entre un núcleo de número de masa A (consideremos N y Z pares), y dos fragmentos de masa , con . Despreciando el efecto de los términos; d, tenemos de (1) que:

M (A, Z) c² ¾2M [(A/2), (Z/2)] c² = usA2/3 (1 ¾ 21/3) + ucA-1/3Z² (1¾2-2/3)

(5)

Como (1 ¾ 2^1/3) < 0 y (1 ¾ 2^-2/3)> 0, el signo de (5) dependerá de cuál de los coeficientes de los paréntesis es mayor. Para núcleos pesados, el término electrostático UcZ²A^-1/3 es mayor que el término de tensión superficial UsA^2/3, y el miembro izquierdo de (5) es positivo, lo que implica que la fisión de un núcleo pesado es exoérgica.

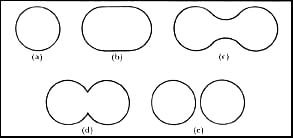
Para el uranio se puede calcular de (5), que la fisión libera cerca de 200 MeV y teniendo en cuenta esa diferencia de energía, nos preguntamos qué impide que el núcleo de uranio se fisione inmediatamente, y que el uranio hubiera desaparecido de La Tierra. Aquí el modelo de la gota de líquido vuelve a ayudarnos.³ Al deformarse la gota de líquido, sigue los pasos de la Figura 2. Al principio, al alargarse la gota disminuye la energía electrostática, pero aumenta la tensión superficial, y un cálculo elemental para un elipsoide muestra que para un núcleo como el uranio, aumenta más rápidamente la tensión superficial que lo que disminuye la repulsión electrostática, de manera que la energía total del núcleo aumenta con la deformación hasta que el núcleo toma la forma (d) de la Figura 2 en que los fragmentos están en contacto. Posteriormente, disminuye la energía al disminuir la repulsión electrostática sin cambiar la tensión superficial. Si designamos por r a un parámetro que mida la deformación del núcleo, y posteriormente la distancia entre los fragmentos del mismo, la variación de la energía con la deformación está indicada por la curva (a) de la Figura 3, en la que el valor r = R corresponde al radio del núcleo no deformado. De la curva (a) se ve claramente que, por lo menos desde el punto de vista de la mecánica clásica, el núcleo es estable contra la fisión, a pesar de que la energía de los dos fragmentos es menor que la del núcleo original. Si en lugar de una curva del tipo (a), tuviéramos una del tipo (b) o (c) de la Figura 5, cosa que ocurriría para núcleos con cargas bastante mayores que las del uranio, los núcleos serían inestables a la fisión. La última parte de la curva (a) proviene simplemente de la energía electrostática de repulsión entre los fragmentos y por lo tanto, va como r^-1.

Figura 2.

De la curva (a) en la Figura 3, vemos que al núcleo hay que proporcionarle una energía DE para que ocurra la fisión, y se puede estimar esa energía de la diferencia de energías entre los dos fragmentos en contacto de la Figura 1(d) y el núcleo original de la Figura 2 (a). Esta estimación puede hacerse con ayuda de la fórmula (5), si le agregamos la energía electrostática de dos cargas cuyos radios son y que está en contacto, de manera que de (2) y (5) se tiene:

DE = (5/6) (Z/2)² (A/2)-1/3 Uc ¾{M(A, Z) ¾ 2 M [(A/2), (Z/2)]}c²

(6)

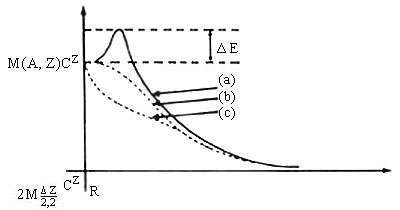
Figura 3.

De (6), y con algunas correcciones apropiadas para los núcleos pesados,³ se estiman las energías DE dadas en el primer renglón de la Tabla 1:

TABLA 1

	92U236	92U236	90Th233
DE (Mev)	5.2	5.8	6.8
Eexc (Mev)	6.4	5.2	5.2

TABLA 2

Th232 + n ® Th233 ® -Pa233 ® -U233	1.63 x 105 años
U236 + n ® U239® -Np239 ® -Pu239	2.41 x 104 años

¿En qué forma podemos proporcionar a los núcleos la energía DE que necesitan para que se produzca el proceso de fisión? El método más directo es el de bombardearlos con neutrones produciendo, como habíamos indicado antes, un núcleo compuesto de A + 1 nucleones. Este núcleo compuesto no se encuentra en su estado de más baja energía sino en un estado excitado, y en el supuesto que la energía cinética del neutrón sea muy pequeña, esta energía de excitación puede estimarse de la diferencia entre la masa del núcleo original, más la masa del neutrón, menos la masa del núcleo compuesto en su estado base, y todo multiplicado por c² es decir:

Eexc = M(A,Z)c² + mnc² ¾ M(A + 1, Z)c²

(7)

Las masas M(A, Z) y M(A + 1, Z) se obtienen de (2) y las energías de excitación están dadas en el segundo renglón de la Tabla 1.

Cuál es la razón de la diferencia de 1 Mev que se observa⁴ entre la energía de excitación del ₉₂U²³⁶ y del ₉₂U²³⁹. El isótopo 236 del uranio se forma del isótopo 235 con la absorción de un neutrón. Ahora bien, el Uranio 235 tiene N par y Z non, mientras que el U²³⁶ tiene N y Z par. De la fórmula (1) vemos que el término d da una contribución » 1/2 Mev a la energía de excitación. En cambio el U²³⁹ se obtiene del U²³⁸ cuando éste absorbe un neutrón. Como el U²³⁸ tiene Z, N pares, y el U²³⁹ tiene Z par y N non, tenemos de (la) que d da una contribución de » ¾ 1/2 Mev, y de aquí se ve la razón del 1 Mev de diferencia en la E_exc del U²³⁶ y U²³⁹. Comparando E_exc con DE, vemos que U²³⁵, al absorber un neutrón lento, da un núcleo compuesto U²³⁶ con suficiente excitación para fisionarse, mientras que tal cosa no pasa con el U²³⁸ al absorber un neutrón, ya que DE> E_exc para el U²³⁹. Sin embargo, si el neutrón llevara una energía cinética superior a 1 Mev, sí podría dar una energía de excitación suficiente para que se fisionara el núcleo compuesto U²³⁹.

De los materiales presentes en abundancia razonable en la naturaleza, sólo el U²³⁵ es fisionable con neutrones lentos. Sin embargo, las razones expuestas en el párrafo anterior nos hacen ver cómo pueden producirse artificialmente núcleos fisionables con neutrones lentos. En la Tabla 2 indicamos dos reacciones nucleares de interés, una del U²³⁸ que, al capturar un neutrón forma U²³⁹ que se desintegra emitiendo un electrón dando Np²³⁹, y finalmente éste se desintegra emitiendo otro electrón para producir el isótopo 239 del plutonio Pu²³⁹, cuya vida media es 2.41 x 10⁴ años. La otra reacción que ocurre en forma similar, nos da, a partir del ₉₀Th²³² más un neutrón, el ₉₂U²³³, con cuya vida media de 1.63x105 años. Ahora bien, Pu²³⁹ y U²³³ tienen Z par y N non, y los correspondientes núcleos compuestos tienen N, Z par. Como en el caso del U²³⁵ del párrafo anterior, esperaríamos ganar 1 Mev en la energía de excitación por la contribución del término d en (1), y por lo tanto, estos núcleos Pu²³⁹ y U²³³, producidos artificialmente, son fisionables con neutrones lentos.⁴

En la primera mitad de 1939 Bohr desempeñó una vez más el papel de profeta que enseñaba el camino a la tierra prometida. En este caso en la comprensión del fenómeno de la fisión nuclear, como antes lo fue en la estructura del átomo, o dirigiendo las intensas discusiones sobre la interpretación de la mecánica cuántica.

Es difícil darse cuenta hoy en día de la excitación producida por el fenómeno de la fisión nuclear en 1939. Desde el punto de vista de la física ha habido varios descubrimientos, que podríamos llamar "inesperados", cuya importancia es comparable. Pero aquí se tenía la posibilidad de un impacto social inmediato, sobre todo cuando las mediciones y la teoría fueron mostrando que se producía más neutrones que las que se absorbía para fisionar el ²³⁵U. Este resultado puede concebirse desde el punto de vista de la gota de líquido, por las pequeñas gotitas que acompañan a los fragmentos principales cuando ésta se fisiona. Más exactamente argumentos de termodinámica, mecánica estadística y física nuclear⁵ aclararon en pocos meses que los neutrones emitidos en cada proceso de fisión serían suficientes para sostener una reacción en cadena.

Al comprenderse lo anterior la excitación de los físicos empezó a convertirse en preocupación. Rápidamente comprendieron que no sólo se tenía en principio un mecanismo totalmente nuevo para producir energía sino también que se podía elaborar explosivos de potencia increíble.

Bohr regresó a Dinamarca a mediados de 1939 y la guerra y luego la ocupación nazi de su país lo desconectaron de los progresos en el campo de la fisión. El temor de que Alemania, donde habían surgido los conocimientos iniciales en ese campo, a través de Hahn y Strassmann, pudiera desarrollar una bomba, hizo que los físicos norteamericanos y británicos se autocensuraran, en el campo de la fisión y sus aplicaciones. No fue sino hasta 1943, cuando Bohr escapó de Dinamarca a Suecia y de allí en un avión de la inteligencia británica a Inglaterra, cuando se enteró de los enormes progresos realizados en el campo de la fisión nuclear así como de los enormes peligros que implicaban. Como he contado en el prólogo de este libro Bohr, más qué con su conocimiento técnico, ya entonces rebasado, contribuyó con su esfuerzo para tratar de lograr un desarrollo pacífico de la energía nuclear. Si por una vez fracasó, fue por el cúmulo de fuerzas que se opusieron a su acción, y no por falta de dedicación y entusiasmo de su parte.

Fue pues Bohr, como Einstein y algunos de los otros gigantes de la física de nuestra época, un profeta que se preocupó hondamente no sólo del camino futuro de la física, sino del tortuoso que la humanidad sigue en busca de una vida mejor.

NOTAS

1 N. Bohr, Nature 137, 344 y 351 (1936); N. Bohr y F. Kalckar, Klg. "Danske Vid" Selkskab. Math. Phys. Medd. 14, Núm. 10 (1937).

2 F. Weizsacker, Z. Physik 96, 431 (1935).

3 Niels Bohr and J.A. Wheeler, Phys. Rev. 56, 426 (1939)

4 N. Bohr, Phys. Rev. 55, 418 (1939).

5 H.D. Smyth, Rev. Mod. Phys. I7, 351 (1945).