DIÁLOGO ENTRE PIER A. MELLO, OCTAVIO OBREGÓN Y LEOPOLDO GARCÍA-COLÍN
OCTAVIO OBREGÓN.—Respecto a este asunto de la complementariedad que se acaba de mencionar estaba leyendo en una biografía de Bohr cuál fue su actitud, y la de Heisenberg, frente a estos primeros descubrimientos de la falta de causalidad en los procesos atómicos y la imposibilidad de medir simultáneamente observables físicas, cuyos correspondientes operadores matemáticos no conmutan. Se describe la desesperación de Heisenberg que afligía a Bohr. Para tratar de calmar un poco la desesperación de su amigo, como acaba de mencionar Leopoldo, Niels Bohr partió a esquiar a Noruega por unas semanas y en este ambiente se le ocurrió la idea de la complementariedad, que después fue desarrollando y perfeccionando en el curso de los años.
De hecho, la idea fundamental de Bohr, con respecto a esta visión del problema, nació precisamente de la dificultad de compaginar la medición simultánea de dos variables que no conmutan. En vez de considerar esto realmente como una fuente de desesperación y como una limitación parece que le dio la vuelta diciendo que, de hecho, la naturaleza es así, que nos muestra aspectos complementarios. Después insistió mucho, en el curso de los años, acerca de cómo realmente se mide una de las variables y cómo se mide la otra. Insistió muchísimo en el hecho de que para medir aquí necesitas un aparato, para medir allá, necesitas otro aparato que, en realidad, es mutuamente excluyente con el primero. Entonces, no hay que persistir en medir uno junto con el otro precisamente porque las dos mediciones son mutuamente excluyentes.
Desde luego, este principio de complementariedad parece tener un papel muy importante en la física y en especial en la mecánica cuántica. Me gustaría que habláramos un poco de la función de onda que habíamos mencionado; es decir, qué relación tiene esta no conmutatividad de dos variables físicas que tenemos que medir independientemente con lo que ya aquí se ha mencionado. Qué es esa ecuación de ondas de Schröedinger y cómo se puede interpretar; entonces aquí te pediría, Pier, que nos dijeras algo sobre la relación del principio de complementariedad y la función de onda.
PIER A. MELLO.—Bohr regresó de sus vacaciones con la idea de la complementariedad y puso en efervescencia al Instituto de Copenhague a través de acaloradas discusiones. Como dato anecdótico, en una ocasión había en la biblioteca del Instituto una gran discusión entre los estudiantes acerca de cómo se podía entender la complementariedad. Con un cierto sentido del humor, Bohr les dijo que es imposible que alguien pueda hacer una reverencia a una persona sin al mismo tiempo darle la espalda a otra: esto es parecido a lo que le pasa al electrón, cuando dos variables no conmutan y por tanto no son medibles al mismo tiempo.
Quisiera mencionar, además, un punto que, para un estudiante que por primera vez se acerca a la mecánica cuántica (MQ) (¡y a veces mucho después también!), es realmente dramático.
Posición y momento "no son medibles simultáneamente", en el sentido de que, para una función de onda dada, las dispersiones de x y p no pueden ser arbitrariamente pequeñas, sino deben satisfacer la desigualdad de Heisenberg. Pero la Escuela de Copenhague va mucho más allá y dice que posición y momento no están simultáneamente definidos para la partícula: o sea, el electrón no posee una posición y una velocidad al mismo tiempo.
A Einstein le molestó profundamente este punto de vista. Concretamente, tomó el ejemplo del decaimiento de un núcleo radiactivo: un emisor de alfas, por ejemplo. Como Einstein no podía creer que el instante del decaimiento de ese núcleo no estuviera definido, propuso que la función de onda describiera no un sistema, sino un conjunto representativo o ensemble de ellos. Entonces el instante de decaimiento estaría perfectamente definido para cada sistema, pero tendría una dispersión sobre los miembros del ensemble.
LEOPOLDO GARCÍA-COLÍN.—Un
comentario muy breve con respecto al principio de complementariedad. Yo confieso
que cuando estudié mecánica cuántica me pasó un tanto inadvertido. Usualmente
en los cursos tradicionales se enseña mucho la herramienta matemática pero todos
estos aspectos conceptuales se dan por un hecho; es decir, se da por sentado
que son correctos o simplemente no se mencionan. Con respecto al concepto de
la complementariedad hay un punto que vale la pena sacar a colación relativo
a la función de ondas. De hecho voy a lanzar una duda, que es la siguiente:
en conexión con la función de onda, para Bohr era muy claro que dicha función
debe describir un campo de probabilidad; sin embargo, muy detrás en su mente
por lo que he podido ver, ahora que he tenido que repasar estos conceptos, él
tenía también bien arraigado en la mente que la frecuencia que aparece en la
fórmula e = hv, la frecuencia de los cuantos de luz es un concepto óptico;
sólo se puede definir usando las leyes de la electrodinámica clásica, que están
basadas en el principio de superposición; es decir, si no aceptamos el principio
de superposición en la teoría de Maxwell, tenemos que hacer una electrodinámica
nueva, por lo menos distinta a la que conocemos. De aquí que debe existir una
relación un tanto profunda entre el principio de complementariedad y lo que
quizá podríamos llamar el principio de superposición que después se usa, claro,
en la mecánica cuántica. Octavio comentará algo al respecto.
OBREGÓN.—Si, yo quisiera tomar el punto del principio de superposición y la función de onda y advertir que voy a intentar aquí representar el papel de abogado del diablo con respecto a algunos aspectos de la escuela de Copenhague. Primero, deseo recordar que en una serie de problemas físicos como por ejemplo la descripción de algunos sistemas que se utilizan en estado sólido, los sistemas cuánticos grandes, como los superconductores utilizamos más bien teorías de tipo hidrodinámico para su descripción. A pesar de que entendemos básicamente lo que es una función de Bardeen, Cooper y Schrieffer para la descripción microscópica cuántica del sistema, no trabajamos normalmente con esta última para describir el comportamiento de este tipo de sistemas físicos. Lo anterior no es un problema de principio pero muestra que la función de onda no es el camino más útil para describir al sistema. Así, en esta clase de problemas particulares, al describir al sistema con otros principios físicos y ecuaciones en general no lineales, la pregunta del principio de superposición en la mecánica cuántica fundamental no es relevante.
Por otra parte, y a nivel más fundamental, la función de onda normalmente se
escribe como una suma de ciertos coeficientes por otras funciones de onda, es
decir, como una superposición de funciones de onda. Poniéndolo de manera más
ilustrativa sí u: es nuestra tundan de onda, ésta se puede escribir como
donde C1, C2, C3,... son constantes y
y1, y2,
y3,... representan
las funciones de onda que al superponerse linealmente nos dan y. Los
puntos suspensivos nos dicen que las Ci y yi
son en general mucho más que sólo tres. Ahora, la interpretación de Copenhague
de la mecánica cuántica nos dice que siempre tenemos un observador macroscópico
que se comporta clásicamente además del sistema cuántico que queremos estudiar.
La función de onda ya no va a consistir en varias funciones de onda sino se
va a colapsar a una sola. A cuál de los elementos de la superposición
se va a reducir eso no lo sabemos. Uno entonces asigna una distribución de probabilidades
a los posibles resultados del experimento
es decir, la probabilidad de que nuestra función de onda se colapse solo a, digamos y3 es ½C3½². Por este motivo el aparato macroscópico de medición no puede decidir qué valor va a encontrar para el sistema observado y se dice que éste entra entonces en un estado de esquizofrenia.
Este colapso y la asignación de pesos estadísticos no son una consecuencia de la ecuación de Schrödinger. Provienen de una metafísica externa a priori a la que se permite actuar en ese momento y suspender la ecuación de Schrödinger (o reemplazar condiciones a la frontera en su solución por aquellas del vector de estado colapsado). El punto de vista de Copenhague da la impresión de que el colapso de la función de onda y ésta misma están sólo en la mente. Si esto es así, ¿qué sucede con la realidad?; ¿cómo puede uno entender y describir el mundo objetivo que claramente nos rodea? Einstein se opuso hasta su muerte a esta solución metafísica de la escuela de Copenhague. ¿Querrías tú comentar algo al respecto Pier?
MELLO.—Algunas de estas ideas se pueden ilustrar muy
bien con el famoso ejemplo del "gato de Schrödinger". En un cuarto están
un gato y una substancia radiactiva; junto a ésta hay un contador Geiger conectado
a un martillo que, bajo una descarga del contador, rompe un frasco de veneno
y el gato muere. Si al cabo de una hora hay 50% de probabilidad de que uno de
los núcleos radiactivos decaiga, ¡la función de onda será una combinación lineal
del gato vivo y del gato muerto en iguales proporciones! Esta situación es incomprensible
si aplicamos la función de onda a un sistema. Si la aplicamos a un ensemble,
nos encontraremos vivos al 50% de los gatos y muertos al otro 50% y la situación,
cabe decir, tiene perfecto sentido.
OBREGÓN.—Bueno Pier, si uno acepta que la función de
onda describe a un ensemble y no a un sistema, como tú has mencionado
que Einstein lo propone, las cosas mejoran y las Pi
= ½Ci½²que yo he
mencionado serían en tu ejemplo del "gato de Schrödinger" solo dos cada
una con un valor de 0.5. Sin embargo, en la interpretación tradicional de la
Escuela de Copenhague el colapso de la función de onda existe aun para un solo
sistema y es una proposición no contenida en la ecuación fundamental de la teoría,
la ecuación de Schrödinger. Esta proposición me parece a mí especialmente
fuerte y quizá no necesariamente la única alternativa para interpretar la mecánica
cuántica. Más adelante mencionaré en especial una propuesta de interpretación
alterna, aunque existen aún otras más.
Bryce de Witt dice lo siguiente respecto a la creencia que la mayoría de los físicos tenemos de ser fieles seguidores de la Escuela de Copenhague: "Al hablar de los seguidores de esta interpretación es importante distinguir los seguidores activos del resto, y darse cuenta que aun la mayoría de los autores de libros de texto no están incluidos en el primer grupo. Si se hiciera una encuesta entre los físicos, la mayoría profesaría ser miembro del grupo convencionalista, así como la mayoría de los norteamericanos proclamarían su creencia en la declaración de los derechos del hombre, independientemente de que la hayan leído. El gran problema en tratar con los activistas es que ellos también cambian las reglas del juego pero, contrariamente a Wigner o Bohr por ejemplo, pretenden no haberlo hecho."
MELLO.—¿Qué es lo que te molesta particularmente del colapso? ¿Cuál es el punto fundamental que crees que es inconveniente, o inadecuado?
OBREGÓN.—En el contexto de la mecánica cuántica convencional,
especialmente acompañando esta idea del ensemble que tú mencionaste,
las cosas no parecen funcionar mal. Sin embargo, siendo la idea del colapso
una proposición más allá de la ecuación básica de la teoría, la ecuación de
Schrödinger, podemos preguntarnos qué otras propuestas o interpretaciones
podrían ser válidas y adecuadas y acompañar a la ecuación de Schrödinger
en una diferente interpretación de la mecánica cuántica. Más tarde me referiré
a un sistema, el Universo, para el cual es especialmente conveniente modificar
la interpretación usual de la mecánica cuántica.
MELLO.—Un punto que a mí sí me molesta es el siguiente: en la mecánica cuántica convencional se supone que después de una medición el sistema se encuentra en un estado mixto. Este postulado fundamental aparece, por ejemplo, en el libro de Von Neumann, en el capítulo sobre "Procesos de medición". Por otro lado, Wigner demuestra que no es compatible con las ecuaciones de movimiento de la mecánica cuántica suponer que el estado del objeto más aparato es, después de una medición, una mezcla de estados, cada uno con una posición definida de la "aguja" del aparato.
De los dos cambios que puede sufrir la función de onda, el continuo, descrito por la ecuación de Schrödinger, y el discontinuo, producido por un proceso de medición, el segundo no parece estar entendido.
Tal vez el carácter macroscópico del aparato sea esencial para describir este cambio irreversible a un estado mixto, y la situación sea semejante a la que ocurre en la mecánica estadística, cuando se quiere hacer compatible la irreversibilidad macroscópica con la reversibilidad de las leyes de movimiento microscópicas.
GARCÍA- COLÍN.—Pero ¿qué se insinúa entonces, o que se sugiere de esto?; que si yo mido e interpreto la medición en términos de un ensamble el resultado de la medición va a ser uno distinto a si uso simplemente el principio de superposición en términos del colapso de onda de que estaba hablando Octavio.
MELLO.—La manera como se aplican estas ideas se puede
ilustrar, por ejemplo, en el experimento de las dos rendijas. Originalmente
la función de onda es la superposición lineal y=
a1y1
+ a2y2
(donde los índices refieren a los dos agujeros) y se observa interferencia
en la pantalla. Si se quiere medir porque agujero paso el electrón, el estado
se vuelve una mezcla de y1
y y2 con
probabilidades ½a1½2,
½ a2 ½²,
y se pierde la interferencia. Este cambio no es descriptible con una dinámica
lineal como la mecánica cuántica.
El problema es todavía más desconcertante. Aun si suponemos que la interacción sistema-aparato cambia la función de onda ½y apar> ½ y sist> en ½yapar> ½ysist>, la probabilidad de encontrar un hamiltoniano (en el sentido de matrices estocásticas) que haga este cambio es cero.
GARCÍA- COLÍN.—Quizás, Octavio, podrías explicarnos porque consideras que la interpretación usual de la mecánica cuántica no es adecuada en la cosmología cuántica.
OBREGÓN.- SÍ, con gusto. La electrodinámica cuántica, como sabemos, es una teoría importantísima que nos enseña a pensar que la interacción entre dos partículas cargadas no la debemos interpretar sólo como acción a distancia como es el caso de la ley de Coulomb (y de la gravitación universal) sino que la interacción entre dos electrones, que producen el campo, sucede porque intercambian fotones (que transportan el campo) entre ellos. De este tipo de descripción podemos nuevamente en un límite clásico" recuperar, por ejemplo, la ley de Coulomb. Nos gustaría seguir los mismos pasos que hemos aprendido en la electrodinámica para lograr construir una gravitación cuántica. Las masas generarían el campo y los "gravitones" lo transportarían. No hemos logrado, por motivos de principio y técnicos, construir una gravitación cuántica y probablemente la respuesta esté por una parte en una teoría que contenga otros campos (una teoría unificada) y quizá en un entendimiento más profundo, a nivel elemental microscópico, del origen y papel de la gravitación.
Un primer paso para tratar de entender lo que debe ser una gravitación cuántica consiste en estudiar los objetos que la gravitación describe como agujeros negros, o bien el mismo Universo (la teoría de la gravitación describe bien su expansión) y entender qué es y qué significa la función de onda asociada a cada uno de estos objetos.
Si el Universo va a ser nuestro sistema cuántico ¿cuál es el aparato macroscópico clásico que vamos a usar para hacer mediciones, de acuerdo con la mecánica cuántica tradicional? Todos estamos dentro del Universo, nadie está fuera. Tenemos que buscar alternativas a la mecánica cuántica tradicional.
Estas alternativas existen; una de las más sorprendentes se debe a Hugh Everett. Él afirma que se puede construir un esquema en el que:
i) Toma el formalismo matemático de la mecánica cuántica como está sin agregarle nada.
ii) Niega la existencia de un mundo clásico separado.
iii) La función de onda nunca colapsa.
Everett necesita definir lo que llama el estado relativo, es decir, tiene que definir la función de onda como producto de una cierta función del sistema por la correspondiente del aparato y alega que la mecánica cuántica provee su propia interpretación.
De acuerdo con esta interpretación, el Universo está definido por una función de onda similar a la que introdujimos anteriormente pero de mucho mayor complejidad. El Universo está dividiéndose constantemente en un número enorme de ramas, resultando todas de las interacciones de mediciones entre sus miriadas de componentes. Más aún, toda transición cuántica que ocurre en cada estrella, en cada galaxia, en cada esquina remota del Universo está dividiendo nuestro mundo local en la Tierra en millones de miriadas de copias de él.
Por fabuloso que lo anterior parezca, el formalismo de esta teoría ha sido tomado en serio por un grupo considerable de físicos prestigiados. Esta propuesta no sólo vale para el Universo sino para cualquier sistema cuántico incluyendo el aparato de medición.
Antes de pasar el micrófono a Pier quisiera insistir en que existen otras alternativas que no describí aquí. Sin dar ningún detalle por falta de tiempo, puedo mencionar que el profesor Bell, autor de la famosa desigualdad de Bell, ha inventado un esquema alterno a la mecánica cuántica llamado la onda piloto.
MELLO.—Sólo quiero mencionar una anécdota. Hace diez o doce años apareció en Physics Today un artículo de DeWitt sobre el rompimiento en varios universos que mencionas. Al mes siguiente un lector, en carta al director, invita a los defensores de esa teoría a no preocuparse si algún día tuvieran un accidente de avión al regresar a su casa, ¡ya que en algún otro universo estarían perfectamente a salvo!
A parte la broma anterior, ¿tú crees que tenga sentido la afirmación de que la mecánica cuántica contiene su propia interpretación? Yo no entiendo cómo una teoría pueda interpretarse a sí misma.
OBREGÓN.—Se asegura sólo que la interpretación probabilística convencional de la mecánica cuántica emerge del formalismo mismo. No tiene implicaciones filosóficas más allá de esta última afirmación.
MELLO.—Otra alternativa para tratar este problema, y que entiendo aún menos, es la propuesta de Wigner de que la interacción entre la mente de un ser viviente y la naturaleza inanimada podría ser la responsable del colapso de la función de onda.
GARCÍA-COLÍN.—Quisiera hacer un comentario, volviendo a lo que dijo Octavio, no en cuestión de la gravitación, sino desde el punto de vista de las variables ocultas. Es bien sabido que el primero quizás, y si no el primero el opositor más consistente de Bohr fue Einstein. Él nunca creyó en esta interpretación, esta incurabilidad de la amibiasis a que nos hemos referido antes. Con base en la llamada paradoja de Einstein, Podolsky y Rosen, se ven claramente los argumentos que daba Einstein intentando buscar una violación del principio de superposición. Con base en dichos argumentos se cuestiona seriamente no sólo si la mecánica cuántica constituye una teoría completa, sino también la postura de la interpretación probabilística de Bohr y Heisenberg. Esta paradoja, de la cual creo debemos hablar más, desató una serie de posturas diferentes con respecto a la interpretación de la mecánica cuántica, al grado que aún en la actualidad éste es un problema vivo. En efecto, han pasado ya cincuenta años desde que se publicó el trabajo de Einstein, Podolsky y Rosen y todavía seguimos discutiendo cuál es la forma de interpretar la mecánica cuántica. Veamos entonces qué opiniones existen al respecto.
OBREGÓN.—Me gustaría decir, en breves palabras, cómo entiendo las ideas de Einstein, Podolsky y Rosen (EPR). EPR proponen tres postulados que suponen que toda teoría física razonable debe cumplir:
i) La regularidad en las observaciones de los fenómenos es producida por realidades físicas cuya existencia es independiente del observador humano. A este postulado se le llama realismo.
ii) El procedimiento inductivo es válido y puede ser aplicado sin limitaciones. De un número grande y finito de observaciones puede uno concluir reglas (o leyes) que valgan en general.
iii)Se conoce como la separabilidad o localidad de Einstein y se refiere a eventos que han acontecido en diferentes lugares, y dice que cada interacción entre estos eventos a lo más será transmitida con la velocidad de la luz.
Estos tres postulados parecen tan evidentes y naturales que todo científico
los aceptaría sin necesidad, casi, de reflexionar. Sin embargo, basados en ellos
empezaremos suponiendo que podemos medir dos componentes de spin de un
protón de manera independiente. Esta suposición es contraria a la evidencia,
pero simplifica la presentación de la prueba (que puede ser hecha en forma rigurosa).
Supongamos que un aparato de medición registra para un protón las componentes
de spin X+ y Y-. La tercera componente, Z, puede
tener sólo el valor más o menos, esto quiere decir que, la descripción completa
del spin del protón seria X+Y -Z+ o
X+Y-Z-. Si encuentra uno varios protones con
los componentes de spin X+Y- podemos escribir para el
total
El símbolo N(X+Y-) designa el número de protones con la componente de spin X+ y Y-.
Como el orden aquí no tiene importancia podemos por el mismo argumento anterior
escribir
el símbolo³ significa mayor o igual.
Hemos mostrado que N(Y-Z+) es mayor o cuando menos igual a N(X+Y-Z+) y que N(X+Z-) es mayor o igual a N(X+Y-Z-).
es por lo tanto menor o igual a la suma
y por lo tanto vale la desigualdad
Ésta es la llamada desigualdad de Bell que se deduce de los postulados de EPR. De las reglas de la mecánica cuántica se sigue que uno puede elegir los ejes X, Y y Z de tal forma que la desigualdad de Bell no sea válida.
Con base en lo anterior, se han diseñado varios experimentos para investigar si la desigualdad de Bell se cumple o no. Hasta ahora parece que de los primeros siete experimentos, cinco están de acuerdo con la mecánica cuántica y dos con la desigualdad de Bell aunque todavía en particular en estos últimos las barras de error son muy grandes y no se puede decir nada concluyente. Pido a Pier que amplíe este importante punto de las variables ocultas y de la propuesta de Einstein, Podolsky y Rosen.
MELLO.—EI título del artículo de Einstein, Podolsky y Rosen (EPR) es "¿Se puede considerar completa la descripción mecánico-cuántica de la realidad física?". Pocos meses después, Niels Bohr contestó a las objeciones de este trabajo con otra publicación que lleva precisamente el mismo título.
Quisiera resumir el problema EPR en dos ideas fundamentales. La primera, la de completez de la mecánica cuántica (MC), es la conclusión directa del artículo. La segunda la de los aspectos no locales de la MC, no es, para mí, tan directamente transparente del artículo mismo, sino más bien fruto de estudios posteriores.
Completez. EPR dan un criterio de realidad física: "Si
se puede predecir con certeza, sin perturbar al sistema, el valor de una cierta
variable física, ésta es un elemento de la realidad física." Presentan después
un argumento asociado con la medición de posición y momento. Es un poco más
simple repetir el argumento en términos de variables de spin. Pensemos
en una pareja de partículas con s(i)=1/2 (i =1, 2), preparada
con spin total cero. La pareja se desintegra, sus dos componentes se
separan y, cuando están muy lejos una de otra (para evitar cualquier interacción
entre ellas), se mide s(i)z ; el resultado de la medición
permite predecir con certeza, y sin interactuar con la partícula 2, que s(2)z
= s(1)z . Por tanto, sz
es un elemento de la realidad física. Se puede presentar un argumento semejante
para sx, de lo que se concluye que sz y sx
son elementos de la realidad. Pero la MC especifica, a través de sus funciones
de onda, una o la otra de esas dos cantidades; por lo tanto, la MC sólo nos
da una descripción incompleta de la naturaleza.
Bohr replicó diciendo que lo se puede separar, en el argumento, al sistema del aparato de medición, y se necesitan aparatos mutuamente excluyentes para medir sz o sx.
No localidad. Supongamos, como en la interpretación copenhaguense, que los observables asociados a dos operadores que no conmuten no estén simultáneamente definidos: es sólo en el momento de la medición que el sistema toma la decisión de exhibirnos sx, o sy, o sz. Entonces encontramos una situación curiosa como la siguiente. Las partículas 1 y 2 ya están muy lejos. Si mido s(1)z y encuentro + 1/2, al medir s(2)z encontraré necesariamente - 1/2. Pero si mido s(2)z y encuentro + 1/2, al medir s(2)z encontraré a veces + 1/2, a veces - 1/2. Esto es precisamente lo que pasaría en las partículas clásicas cuyo momento angular tuviera valores definidos en las tres direcciones. La correlación observada sería una consecuencia de la conservación del momento angular. Pero si un valor específico de una cierta proyección del spin ocurre sólo en el momento de medir, ¿cómo sabe la partícula 2 a qué ensemble debe pertenecer? ¿De qué manera pudo 1 comunicarle a 2 qué decisión tomar?
Un tipo de variables ocultas que se han inventado cumple precisamente con la tarea de evitar esa no-localidad, produciendo la correlación adecuada entre las variables a nivel cuántico.
GARCÍA-COLÍN.—¿Qué nos podrías decir sobre algún experimento reciente realizado para aclarar algunas de estas cuestiones?
MELLO.—En un número reciente de Physics Today, Mermim comenta los resultados de un experimento realizado en Orsay. Quisiera resumir algunas de las ideas presentadas en ese artículo.
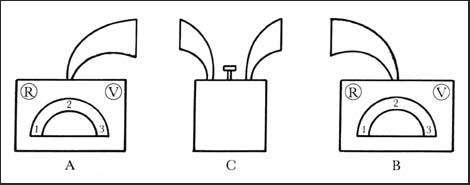
Un aparato EPR se puede esquematizar de la siguiente manera. A
y B representan dos detectores: cada uno tiene un switch que se puede colocar
en tres posiciones diferentes (que van a corresponder a las tres proyecciones
del spin, aunque A y B se pueden seguir considerando como cajas negras)
y dos focos, uno rojo y uno verde (que van a corresponder a si se observa +
1/20 - 1/2 para un detector, y al revés para el otro). En medio está una fuente
C, que se dispara apretando el botón que está sobre ella. Se varían al azar
las posiciones de los switches cada vez que se dispara la fuente y se observa
cuál foco (R o V) se prende en cada detector. Un fragmento típico de una corrida
muy larga se ilustra a continuación:
| 31 RR |
22 VV |
33 VV |
| 33 VV |
11 RR |
21 VR |
| 33 RR |
33 VV |
13 VR |
| 12 VR |
31 VR |
23 VR |
Se observa que R y V ocurren enteramente al azar. Por ejemplo, la mitad de las veces los dos focos son del mismo color.
Sin embargo, si aislamos en el listado anterior aquellas mediciones en que
el switch está en la misma posición en los dos detectores, se observa que en
cada caso se prendió un foco del mismo color (en la aplicación, esto va a corresponder
a que los dos spines son necesariamente opuestos). Si seguimos considerando
al sistema como un conjunto de cajas negras, nos preguntamos qué mecanismo podría
causar la correlación de colores que se menciona. Si los dos detectores no se
comunicaron entre sí, las dos partículas tuvieron que haber traído desde la
fuente un "manual de instrucciones". Supongamos que la "instrucción" haya sido
RVR, lo que significa que si el switch está en la posición 1, se prende
el foco rojo, en la 2 el verde y en la 3 el rojo (en la aplicación, las dos
partículas tienen las 3 proyecciones del spin bien definidas ![]() y
y
![]() ,
respectivamente). Esto explica la correlación mencionada arriba, En total, 5
veces de 9(11, 22, 33, 13, 31) se observa el mismo color. Haciendo el mismo
razonamiento para otras instrucciones, se llega a la conclusión de que la fracción
de veces que debería observarse el mismo color es mayor que 1/2, ¡mientras que
experimentalmente es 1/2! Este es un ejemplo elemental de la desigualdad de
Bell que Octavio mencionó antes.
,
respectivamente). Esto explica la correlación mencionada arriba, En total, 5
veces de 9(11, 22, 33, 13, 31) se observa el mismo color. Haciendo el mismo
razonamiento para otras instrucciones, se llega a la conclusión de que la fracción
de veces que debería observarse el mismo color es mayor que 1/2, ¡mientras que
experimentalmente es 1/2! Este es un ejemplo elemental de la desigualdad de
Bell que Octavio mencionó antes.
Este resultado me parece muy molesto, porque el haber abierto la posibilidad de que sx, sy, sz existan al mismo tiempo nos lleva a un resultado que contradice el experimento (cuyas barras de error, por ejemplo, habría que analizar con cuidado) y éste, a su vez, coincide con las predicciones de la mecánica cuántica.
Se podría objetar que querer que sx, sy, sz existan al mismo tiempo es una extensión inadecuada de los conceptos clásicos, ya que el spin, con su propiedad de que cada proyección solo valga + 1/2 o -1/2 y su magnitud valga 1/2, ¡no es un momento angular clásico! Sería interesante ver si con las variables x, p, por ejemplo, el experimento otra vez viola la desigualdad de Bell y sigue la MC.
Feynman, en su librito The Character of the Physical Law, expresa su creencia de que no es posible la existencia simultánea de dos variables cuyos operadores no conmuten. Ilustra esto con el experimento de las dos rendijas y parece llegar a la conclusión de que el simple hecho de que el electrón trajera instrucciones desde la fuente acerca de que rendija escoger, ¡destruiría la interferencia en la pantalla!
GARCÍA-COLÍN.—Ha habido críticas a la desigualdad de Bell. ¿Podrías mencionar alguna?
MELLO.—Se ha mencionado que en la demostración de la desigualdad de Bell implícitamente se supone la localidad de las variables ocultas, y que queda abierta la posibilidad de la no localidad. También se ha alegado que la densidad de probabilidad que se usa para las variables ocultas se toma de estado inicial del sistema y el proceso de medición no parece entrar en juego en la prueba.
GARCÍA-COLÍN.—Respecto a este problema de las variables ocultas, ¿tienes algún comentario?
MELLO.—Quisiera comentar sobre una opinión que a veces se escucha, en el sentido de que con la introducción de las variables ocultas no se ha eliminado el azar, sino que éste se ha pasado a otro nivel.
A mí me parece que ese no es el punto. Si se logra introducir variables ocultas l, se habrá logrado que x, p estén definidas simultáneamente a un nivel subcuántico; un promedio sobre l reproduciría la MC o alguna generalización de ella, tal como en mecánica estadística se obtiene la termodinámica promediando sobre las variables microscópicas, que estarían "ocultas" a nivel macroscópico. Desde luego habría que ver si las predicciones resultantes concuerdan con el experimento, como mencioné más arriba en conexión con el experimento de Orsay.
La idea de trabajar en el espacio fase, como se hace en física clásica, es muy atractiva. Ha habido más de un intento en el pasado. Sin embargo, un teorema debido a Wigner, que indica que no se puede construir dentro de la MC una densidad de probabilidad positiva definida sobre el espacio fase (por ejemplo, la "distribución de Wigner"), parece limitar esta posibilidad. Pero Wigner supone, en su prueba, que tal densidad es una función cuadrática de la función de onda; esta suposición se puede relajar y así se abre la puerta a una serie de posibilidades muy interesantes.
Finalmente quisiera mencionar el siguiente punto. Aun en mecánica clásica, los sistemas no integrales son deterministas, mas no calculables: parece que sólo se puede dar una descripción probabilística en el espacio fase (sistemas caóticos). Si ahora pensamos en el punto de vista de la electrodinámica estocástica para describir a los sistemas microscópicos, un electrón estaría sujeto a un potencial estocástico proveniente, quizá, del resto de materia en el Universo: seguramente un problema tan complejo como éste cae dentro de la categoría de los no integrables mencionados más arriba, donde sólo es factible dar una descripción probabilística del problema. ¡Tal vez no logremos librarnos del azar!