APÉNDICE II

ECUACIONES PARA LA PRESIÓN OSMÓTICA

En el caso de dos soluciones con dos componentes (A y B) en equilibrio a través de una membrana permeable al componente A e impermeable al componente B se tiene que

CBDmB= DPeq

(1)

DmA= 0

(2)

Las dos ecuaciones contienen básicamente la misma información. Para demostrarlo, se utilizará la expresión para el potencial químico,

Dmi = RTD Lnai + Vi Dp

(3)

donde a_i es la actividad y V_i es el volumen molar parcial del componente i. Sustituyendo la ecuación (3) en la ecuación (1) y considerando el equilibrio, tenemos que:

CBDmB = RTCBDLnaB + CBVBDPeq

(4)

Por otra parte, la ecuación de Gibbs-Duhem establece que

CBDLnaB = — CADLnaA

(5)

con lo cual, la ecuación (4) se puede escribir

CBDmB = — CARTDLnaA + VBCBDPeq=DPeq

y de donde podemos obtener

— RTCADLnaA — (1 — CBVB)DPeq = 0

(6)

Dado que C_A V_A = l — C_BV_B se tiene que (6) se escribe como

RT DLnaA + VADPeq=0

(7)

Lo que de acuerdo con la ecuación (3), lleva a la ecuación (2). La presión osmótica puede estimarse de acuerdo a la ecuación (7)

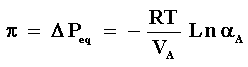(8)

En el caso particular de que tomemos en cuenta una solución diluida, el logaritmo de la actividad del solvente en solución puede escribirse como el negativo de la fracción de moles de cada componente en la solución.

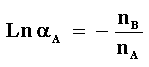
donde n_A es el número de moles del solvente en la solución y n_B el número de moles del soluto. Ahora bien, V = V_An_A es el volumen total y la ecuación (8) se convierte en

pV= nB RT.

(9)

Es la ecuación de Van't Hoff que muestra la semejanza de la presión osmótica con la presión de un gas ideal.