IV. DESCRIPCIÓN DEL FLUJO OSMÓTICO

EN ESTE capítulo se discutirá la caracterización de un sistema fuera de equilibrio y la relación de ésta en el contexto de membranas y el flujo osmótico.

La termodinámica clásica, que ya hemos mencionado antes, se refiere a sistemas fluidos en estado de equilibrio, definido éste, como el estado cuyas variables no cambian con el tiempo. Asimismo se observa que esas variables tampoco cambian con la posición. Es decir, la termodinámica de equilibrio es compatible con sistemas fluidos homogéneos y estados independientes del tiempo.¹

La propiedad de homogeneidad, de la que hacemos referencia aquí, está asociada al equilibrio, porque cualquier cambio en los valores de las variables de estado producirá un proceso de transporte, que a su vez causará cambios en el tiempo de tales variables.

Ahora bien, si consideramos a un sistema termodinámico fuera de equilibrio como uno inhomogéneo, pensaremos en las alteraciones que de forma diversa y distinta aparecen a lo largo y ancho del sistema. Estas alteraciones indican desigualdades en los valores de las variables que describen la situación y las cuales cambiarán con el tiempo.

La descripción de los efectos de las alteraciones del sistema fuera de equilibrio se efectúa en forma natural considerando las diferencias en los valores de las variables de estado y los flujos asociados, para todas las localidades del sistema. Los efectos de los flujos, como se dijo antes, es modificar los valores de las variables de estado, y ocurre de manera tal, que las diferencias disminuyen y el sistema evoluciona al estado de equilibrio homogéneo.

La descripción formal de un sistema fuera de equilibrio se basa en la suposición de que la relación matemática entre los flujos y las fuerzas termodinámicas es de carácter lineal. Aunque esta hipótesis restringe la validez de la teoría en cuanto a la cercanía del equilibrio, se tiene la ventaja de construir una teoría simple y lógicamente consistente.

En lo que respecta al caso de las membranas, hay generalmente tres tipos de esta asociación lineal, tal como se observa en el cuadro 1.

CUADRO I.

Ley de Fick	Relación lineal entre flujo de difusión y la diferencia de concentraciones
Ley de Ohm	Relación lineal entre el flujo de cargas y la diferencia de potenciales eléctricos
Ley de Poiseuille	Relación lineal entre el flujo volumétrico y la diferencia de presiones

La teoría que da lugar a estas hipótesis acerca de las relaciones lineales se llama "Termodinámica irreversible lineal" y fue formulada por L. Onsager en 1931, por uno de sus principales resultados. Así fue como se estableció por primera vez que, dado un sistema fuera de equilibrio en el que están presentes varios tipos de inhomogeneidades en los valores de las variables de estado, un flujo cualquiera, dentro del sistema, es producido por la superposición lineal de todas las fuerzas presentes siempre y cuando, tanto las fuerzas como los flujos posean una misma calidad vectorial (principio de los acoplamientos, previamente introducido por P. Curie en 1908).

Esto significa que hay efectos cruzados, pues un flujo cualquiera puede ser dado por una fuerza que no corresponde al efecto directo. Por ejemplo, un flujo difusivo puede ser causado por un campo eléctrico o por una diferencia de presiones. Otro ejemplo es el flujo volumétrico presente a consecuencia de una diferencia de concentraciones, que es el caso del flujo osmótico (véase la figura 5). ...Al hacerse la distinción entre efectos cruzados, Onsager estableció su reciprocidad. Es decir, la posibilidad de que tales efectos pueden intercambiarse. Así por ejemplo, si una diferencia de temperaturas produce un flujo de cargas eléctricas, por lo tanto es posible que una diferencia de potencial eléctrico produzca una diferencia de temperaturas y por consiguiente un flujo de calor. Estos dos efectos cruzados son conocidos con los nombres de Seebeck y Peltier respectivamente.²

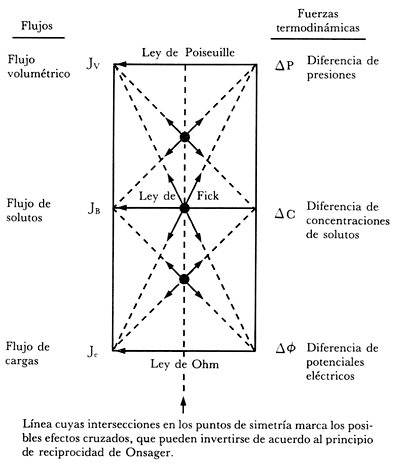
Figura 5. La figura muestra dos cuadrados perfectos compartiendo un mismo lado. Los vértices del lado izquierdo señalan los posibles flujos en el sistema donde las fuerzas son indicadas en los vértices del lado derecho. Las uniones entre vértices de diferentes lados señalan flujos. Las horizontales son los efectos directos y los indicados con líneas de trazos, son los efectos cruzados.

En el caso de las membranas, el hecho que ha provocado muchas horas de discusión entre los fisicoquímicos y los fisiólogos ha sido la correspondencia recíproca de los efectos causados por diferencias de concentraciones y de presiones. Desde 1909 E. G. J. Hartley había demostrado que la presión osmótica y la presión hidrostática son efectos enteramente equivalentes al mover agua a través de una membrana. Otros más hicieron dicho experimento, y aún en 1957-1960 A. Mauro lo repitió hasta entender el mecanismo de acoplamiento entre una diferencia de concentraciones y la generación de un déficit de presión. Este acoplamiento fue interpretado en forma matemática por A. J. Staverman en 1951-1952, utilizando la teoría lineal de procesos irreversibles. Staverman estableció la primera teoría explicativa de las medidas del flujo osmótico y tuvo a bien enseñar las causas termodinámicas de dicho flujo y los acoplamientos entre efectos de una membrana. Asimismo, la comparación de la teoría con el experimento llevó a Staverman a considerar un coeficiente de reflexión que actualmente lleva su nombre, y en el que se toman en cuenta las cualidades de una membrana.

La aplicación de la teoría termodinámica irreversible de transporte fue completada por O. Kedem, A. Katchalsky (1957-1966).

Las ecuaciones básicas que resultan de esta aplicación en membranas son comentadas a continuación para el caso en que hay dos fuerzas termodinámicas dadas por DC_B y DP.

El flujo de soluto (JB) es dado por una superposición de un flujo difusivo y un flujo volumétrico (Jv), donde aparece el coeficiente de reflexión de Staverman (s).

Flujo de	=	Flujo	+	Flujo volumétrico que
soluto (B)		difusivo		afecta al flujo de solutos

JB

=

w DCB

+

CB (1 - s) Jv

(1)

 

En la ecuación C_B es la concentración promedio del soluto en la membrana y DC_B es su diferencia a través de la membrana. Es menester dejar establecido que esta ecuación toma en cuenta la presencia de la membrana como una interfase donde ocurren los procesos de transporte. La membrana está limitada por dos baños en equilibrio termodinámico de manera que los valores de presión y concentración no cambian con el tiempo (véase la figura 6).

Dado que DC = C"_B-C'_B¹0 la membrana se altera por un proceso difusivo, indicado en el primer término de la ecuación (1). De manera que el sistema al que hacemos referencia como fuera de equilibrio es la membrana y está sujeto a las condiciones de las fronteras especificadas por los baños de los recipientes (1) y (2) como se ilustra en la figura 6.

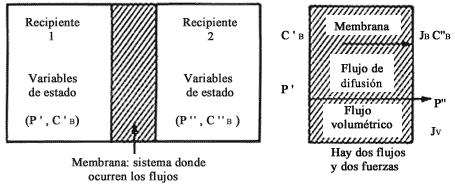
Figura 6. Una membrana separa dos baños con diferentes concentraciones de soluto (C_B) y presiones. En los baños no ocurren procesos y los flujos de intercambio se presentan en el interior de la membrana.

Además de esta contribución al flujo de difusión, disponemos de la originada por la diferencia de presiones DP=P"-P'. Este efecto de acoplamiento se indica en el segundo término de la ecuación (1). El flujo osmótico no aparece en la ecuación (1) en vista de que está asociado al flujo del solvente. Es costumbre no dar la forma explícita de este flujo, sino el correspondiente al flujo volumétrico considerado como la superposición de dos efectos, uno directo debido a la diferencia de presiones y otro cruzado debido a la diferencia de concentraciones; este último es el flujo osmótico. En esta forma el flujo volumétrico se escribe como:

Flujo de	=	Flujo	+	Flujo
volumétrico		Poiseuille		osmótico

Jv

=

-L DP

+

LsRTDCB

(2)

Donde R es la constante de los gases y T la temperatura absoluta; L es el coeficiente de permeabilidad de la membrana.³

En el sistema de ecuaciones (1) y (2) están presentes dos flujos, el difusivo y el volumétrico y dos fuerzas DP y DC. Ahora bien, si se enumeran los coeficientes independientes, se observan sólo tres (w, L y s), siendo que hay cuatro efectos en el sistema: dos directos y dos cruzados, que aparecen en el cuadro superior de la figura 5. Lo que ocurre es que el principio de reciprocidad de Onsager garantiza que el coeficiente de reflexión de Staverman (s) es el mismo en las ecuaciones (1) y (2). Esta situación es compatible con la termodinámica irreversible lineal. No obstante se han dado casos en que este principio deja de ser válido en presencia de membranas. Por ejemplo, en el caso de una membrana muy apretada, casi semipermeable en donde se restringe el paso del soluto (s £ 1) se tiene que el acoplamiento del flujo volumétrico y el soluto (B) se hace muy pequeño y el flujo del soluto en forma mínima se vuelve solamente difusivo (véase la figura 7).

En este tipo de membranas, el efecto cruzado osmótico ocurre correctamente, pero el efecto recíproco originado en el acoplamiento del flujo volumétrico y los solutos se trastoca, ya que afecta a los solutos que pasen y no altera a los solutos que se les impide pasar. En este momento se rompe la simetría en las interacciones soluto-solvente y las relaciones recíprocas de Onsager ya no son válidas, y, por lo mismo, los coeficientes (s) en las ecuaciones (1) y (2) no son los mismos. Este caso ha sido discutido muy recientemente por L. F. del Castillo y E. A. Mason.

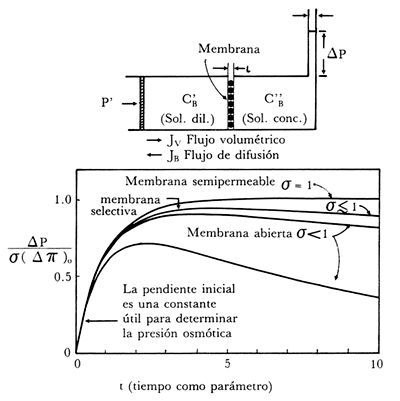
Figura 7. Un diagrama experimental de ósmosis dinámica se observa en la figura superior. La membrana puede ser semipermeable (s = 1), selectiva (s 1) y abierta (s < 1). Las figuras de la gráfica inferior observan la posibilidad de conocer la presión ósmotica inicial s (D p)_º por medio de la pendiente para tiempos pequeños.

En el caso límite de una membrana semipermeable a = 1, debe cancelarse el flujo de difusión del soluto y w = 0, puesto que se impide totalmente el flujo de soluto a través de la membrana. En tal caso la ecuación (2) sólo representa el flujo del solvente.

El otro límite en que s = 0, y las ecuaciones (1) y (2) representan a una membrana muy abierta o a un medio poroso en el que no está presente el efecto osmótico. En tal caso, hay que hacer notar que la ecuación (2) se convierte en la ecuación de Darcy. Se ha supuesto que las variables de estado de los baños a los lados de la membrana no cambian con el tiempo (véase la figura 6), entonces debe tratarse de un caso estacionario, pues los flujos en la membrana deben ser los mismos todo el tiempo. Esta situación es posible si los recipientes 1 y 2 son muy grandes, comparados con la membrana, de tal manera que el resultado de estos procesos de transporte no afecten las variables P y C de cada baño. Esto también puede ocurrir si tomamos en cuenta una escala de tiempo en que los procesos de transporte son sumamente lentos para que afecten las variables de estado. No siempre tendremos este caso, y si las variables P y C dependen del tiempo, podremos observar la evolución del sistema hasta el estado de equilibrio. Tratándose de una membrana abierta en la que tanto los solutos como los solventes pueden pasar, la situación final observará que DP =0 y DC_B=0

En cambio, en el caso de una membrana semipermeable, la situación final de equilibrio estará especificada sólo por la ecuación (2) en la que

Jv=0 y

DP=Dp=RT DC_B

La cual representa la ecuación de Van't Hoff para la presión osmótica entre dos soluciones diluidas con concentraciones C" y C'.

La aplicación de la ósmosis dinámica para medir la presión osmótica sin necesidad de esperar a que el sistema evolucione hacia el equilibrio, se consigue por medio de un análisis de la situación inicial cuando se hace un experimento en que originalmente no hay diferencias de presiones, es decir, DP =0 para un intervalo de tiempo inicial. En tal caso el flujo volumétrico es directamente proporcional a la presión osmótica, pues de la ecuación (2) tenemos

Jv = L(sDp)

si la membrana es semipermeable, s = 1, sólo basta conocer el coeficiente de permeabilidad L para determinar la presión osmótica a partir de las medidas del flujo volumétrico. Pero en caso de que la membrana presente fugas de soluto de un lado a otro de la membrana, s ¹ 1, se encontrará que el valor medido de la presión osmótica (Dp)_exp, no corresponde al valor teórico determinado por medio de la ecuación de Van't Hoff. Esta diferencia observa también la medida del coeficiente de reflexión de Staverman de la siguiente forma:

La medición de s para membranas abiertas es necesaria en la determinación de la presión osmótica de una solución por el método de ósmosis dinámica. En efecto, la medida del coeficiente de reflexión de Staverman permite que a partir de la determinación experimental de la presión osmótica (Dp)_exp se obtenga la presión osmótica teórica o termodinámica.

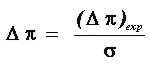
Es el valor teórico de Dp que se relaciona, en el límite de soluciones diluidas, con el peso molecular del soluto (Van't Hoff, 1885).

NOTAS 1 Es posible hablar de inhomogeneidades en un estado de equilibrio, pero deben estar conformadas por medio de constricciones que impidan cambios en el tiempo. Este tipo de inhomogeneidades se excluyen de la presente discusión.

2 La teoría lineal de procesos irreversibles fue desarrollada posteriormente a los trabajos de Onsager. Entre los investigadores de esta línea se encuentra a H. B. G. Casimir (1945), quien generalizó la validez de las relaciones recíprocas de Onsager a toda clase de fenómenos irreversibles, así como a J. Meixner (1941-1943), I. Prigogine (1947) y S. R. de Groot (1950), entre otros.

3 En la derivación de la ecuación (2) hay la suposición de que las soluciones de los baños 1 y 2 son diluidas.