VIII. OTRA VERTIENTE. PLANCK Y LA TEORÍA CUÁNTICA

EN ESTE capítulo haremos una breve descripción de otros desarrollos que se estaban llevando a cabo de manera paralela a los sucesos que narramos anteriormente, y se refieren a la teoría de radiación térmica.

Nuestra historia se remonta al año de 1859 cuando el físico alemán Gustav Kirchhoff presentó un trabajo a la Academia de Ciencias de Berlín que trataba de la emisión y absorción de calor y luz. Kirchhoff demostró, como consecuencia de investigaciones sobre las propiedades de la luz que nos llega del Sol, que si rayos de luz de frecuencia fija inciden sobre un cuerpo, éste absorbe parte del haz incidente. La fracción absorbida por el cuerpo se llama poder de absorción. Cada cuerpo, dependiendo de los materiales de que esté compuesto tendrá su valor particular del poder de absorción. Distintos cuerpos tienen, en general, distintos valores de esta cantidad. Además, el poder de absorción de un cuerpo tiene distintos valores para distintas frecuencias de las ondas de luz que incidan sobre él.

Por otro lado, un cuerpo dado que esté a cierta temperatura fija emite luz. La mayor parte de ella invisible al ojo humano, luz que tiene ondas de muchas frecuencias (figura 20). La fracción de la energía emitida a una frecuencia fija se llama poder de emisión. Al igual que con el poder de absorción, el poder de emisión de un cuerpo, a una frecuencia dada, depende de las características del cuerpo. Distintos cuerpos tienen distintos poderes de emisión, y para un mismo cuerpo, sus poderes de emisión son distintos para distintas frecuencias de la luz.

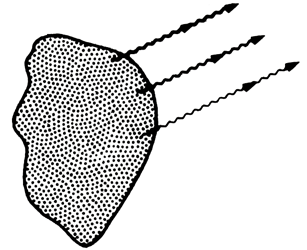
Figura 20. Un cuerpo a una temperatura fija emite radiación electromagnética de diferentes frecuencias.

Sean a_f y e_f los poderes de absorción y emisión de un cuerpo a la frecuencia f, respectivamente. Kirchhoff demostró en su trabajo de 1859 que el cociente de estas dos cantidades, o sea, e_f /a_f tiene el mismo valor para todos los cuerpos que estén en equilibrio a la misma temperatura. Esto significa que si tenemos dos cuerpos a la misma temperatura, pero hechos de distintos materiales y de distintas formas, entonces el cociente arriba indicado (a la frecuencia f) para cada uno de ellos tiene un valor. Kirchhoff demostró que estos valores numéricos son iguales.

Además, el valor del cociente mencionado solamente depende de la frecuencia y de la temperatura. A causa de que este cociente es el mismo para todas las sustancias, es una cantidad universal. A este resultado se le llama la ley de Kirchhoff.

En tiempos de Kirchhoff se conocía solamente la luz visible. Sin embargo, existen otras ondas que tienen frecuencias que no son visibles al ojo humano. Esta radiación es la llamada invisible y consiste en ondas ultravioleta, infrarroja, etcétera. Se ha podido demostrar que la ley de Kirchhoff es también válida para las ondas de la radiación invisible.

Consideremos ahora un cuerpo muy particular que es el llamado cuerpo negro. Éste es un absorbedor perfecto de radiación tanto visible como invisible, a cualquier temperatura. Se usa la palabra negro para denotar a una sustancia que absorbe toda la luz que le llega y no refleja nada de ella, como por ejemplo el carbón. Del trabajo de Kirchhoff se concluye que si un cuerpo es un absorbedor perfecto de radiación a cualquier temperatura, entonces también será un perfecto emisor de radiación.

Apliquemos ahora la ley de Kirchhoff a un cuerpo negro. En este caso, como el cuerpo absorbe toda la radiación que le llega, el poder de absorción es a_f = 1. En consecuencia, el cociente arriba mencionado es igual a e_f . Por lo tanto, el poder de emisión de un cuerpo negro es precisamente la cantidad universal arriba citada. Es justamente por este motivo que se usa el cuerpo negro. Si se tratara de obtener esta cantidad universal usando cualquier otro cuerpo, se tendrían que obtener dos propiedades: los poderes de emisión y de absorción. Para un cuerpo negro esta última es igual a 1.

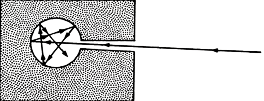
Un ejemplo de cuerpo negro es el formado por una cavidad (figura 21) cuyas paredes se encuentran a una temperatura fija. Las paredes interiores de la cavidad son negras. Este cuerpo tiene un pequeñísima abertura. Cualquier radiación que pueda entrar por la abertura es dispersada en el interior y absorbida por reflexiones repetidas, con la consecuencia de que prácticamente nada de ella puede volver a salir. Es decir, esta cavidad absorbió toda la radiación incidente, con lo cual es un perfecto absorbedor, y por tanto, un cuerpo negro. En consecuencia uno intentaría encontrar el poder de emisión de esta cavidad. Esta cantidad solamente depende de la frecuencia y de la temperatura.

Figura 21 una cavidad puede ser un cuerpo negro.

Si ahora sumamos todas las energías que corresponden a cada una de las frecuencias de la radiación que está dentro de la cavidad se obtendrá la energía total. De acuerdo con la ley de Kirchhoff, la energía total contenida dentro de la cavidad que se encuentra a una temperatura fija solamente dependerá de la temperatura y será independiente de la naturaleza de la pared.

En 1865, John Tyndall, en Inglaterra, llevó a cabo una serie de mediciones sobre la emisión total de energía de un alambre de platino a distintas temperaturas, al hacerle pasar una corriente eléctrica. Al calentarse el alambre emite radiación. Se puede considerar esta radiación como de cuerpo negro. Tyndall encontró que a 1 200ñC (=1 473ñK) el platino emitía 11.7 veces más energía que cuando estaba a la temperatura de 525ñC (= 798ñ K).1 En Viena, Josef Stefan conoció estos resultados y se dio cuenta que el cociente de 1,473 entre 798 elevado a la cuarta potencia es aproximadamente 11.7, es decir,

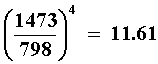
En 1879 concluyó que la energía total de la radiación es proporcional a la cuarta potencia de la temperatura absoluta T. Una verificación independiente de esta conclusión la hizo L. Graetz en Estrasburgo, Francia, en 1880. Experimentos posteriores hechos entre 1897 y 1899 por F. Paschen, O. Lummer y E. Pringsheim, C. E. Mendenhall y F. A. Saunders para diversas temperaturas confirmaron esta dependencia en la temperatura.

Fue Ludwig Boltzmann quien presentó en 1884 una justificación teórica del resultado de Stefan. Boltzmann hizo la demostración con ayuda solamente de razonamientos termodinámicos. A este resultado se le llama la ley de Stefan-Boltzmann.

Nótese que la energía a la que se refiere la ley de Stefan-Boltzmann es la total que emite el cuerpo. En particular, hay que darse cuenta de que la ley de Stefan-Boltzmann no dice nada acerca de las propiedades de la radiación para distintas frecuencias.

Por otro lado, en la última parte del siglo pasado se desarrolló una intensa actividad de investigación experimental de las propiedades de la radiación del cuerpo negro, como se le llamó. En 1880, S. P. Langley, en Estados Unidos, en el curso de investigaciones sobre la radiación solar, inventó el bolómetro, aparato con el que se lograron muy altas sensibilidades en las mediciones de la radiación. Por otro lado, en 1895 Otto Lummer y Willy Wien construyeron por primera vez una cavidad que sirvió de fuente de radiación de cuerpo negro. Desde 1884 se había formado un grupo experimental de investigación en el Instituto Físico-Técnico de Berlín donde además de Lummer también trabajaron E. Pringsheim, H. Rubens, F.Kurlbaum y otros más.

En el año de 1896 W. Wien publicó un trabajo en el que obtuvo la distribución de la energía en la radiación de cuerpo negro, es decir, la energía según la frecuencia de la radiación y de su temperatura. Para ello usó una sugerencia propuesta en 1887 por el físico norteamericano V. A. Michelson que utilizó la distribución de velocidades que había obtenido Maxwell. Así, Wien obtuvo los resultados mostrados en la figura 22. Aquí se muestran varias distribuciones para distintas temperaturas. Nótese que estas curvas tienen la forma general de una campana. Posteriormente, entre 1879 y 1899, Max Planck presentó una derivación más rigurosa de los resultados de Wien.

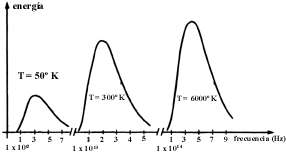
Figura 22. Distribución de Wien para distintas temperaturas. A medida que la temperatura aumenta, el máximo se desplaza hacia mayores valores. Nótense los cambios de escala para la frecuencia.

F. Paschen y H. Wanner hicieron una serie de experimentos muy metódicos que confirmaron los resultados obtenidos por Wien para las frecuencias que corresponden a la luz visible y para temperaturas de hasta 4 000ñC.

El valor de la frecuencia f_m para el cual la distribución adquiere un máximo es distinto para distintas temperaturas. Vemos que al aumentar la temperatura aumenta este valor máximo de f_m. Esto constituye lo que se llama la ley de desplazamiento de Wien. En 1879 Lummer y Pringsheim confirmaron experimentalmente este desplazamiento para temperaturas del cuerpo negro entre 100ñC y 1 300ñC.

Hacia fines de siglo, se realizaron experimentos para valores de las frecuencias mucho menores que las visibles y se concluyó que la ley de radiación de Wien dejaba de ser válida en esos rangos. De hecho, para frecuencias muy bajas había discrepancias muy fuertes con los resultados experimentales.

En junio de 1900 apareció publicado un trabajo del notable físico inglés lord Rayleigh en el que aplicaba el teorema de equipartición de la energía de la teoría cinética a la radiación electromagnética. Su argumento fue muy sencillo: calculó el número de ondas que había en un intervalo muy pequeño de frecuencias y, de acuerdo con el teorema de equipartición de la energía, a cada una de ellas le asignó la misma energía. Así obtuvo una distribución de frecuencias. En la figura 23 se muestran algunas de estas distribuciones para diferentes temperaturas. A esta ley se le ha llamado la ley de radiación de Rayleigh-Jeans. Al comparar con resultados experimentales resulta que la ley de Rayleigh concuerda en la región de muy bajas frecuencias, justamente donde la ley de Wien falla. En las altas frecuencias, es la ley de Rayleigh la que entra en falta ya que la distribución crece sin cesar, hecho que no es aceptable. Pero es en la región de altas frecuencias en donde la ley de Wien concuerda con la realidad.

Como resumen de lo anterior podemos decir que hacia la última mitad de 1900 se sabía que las leyes de Wien y de Rayleigh no podían describir los resultados experimentales obtenidos para la distribución de la radiación de cuerpo negro. Se ve que, en cierto modo, son complementarias. Lo que hacía falta era una ley que para frecuencias grandes concordara con la de Wien, mientras que a bajas frecuencias concordara con la de Rayleigh.

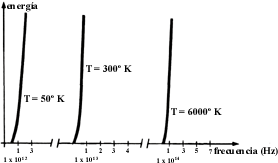
Figura 23. Distribución de Rayleigh para distintas temperaturas. Estas distribuciones no tienen máximo. Nótense los cambios de escala para la frecuencia.

Max Planck (1858-1947) fue alumno de Kirchhoff y trabajó durante mucho tiempo en la teoría de la termodinámica. Los trabajos de R. Clausius, uno de los científicos que desarrollaron esta disciplina, tuvieron una influencia muy grande sobre su trabajo posterior. En particular, Planck elaboró con mucha precisión la segunda ley de la termodinámica que había formulado Clausius. Durante gran parte de la primera mitad de su vida científica, Planck se mostró hostil hacia la teoría atómica. Desarrolló trabajos, por ejemplo sobre transiciones de fase, como la evaporación, en los que enfatizó que no había hecho ninguna suposición sobre la constitución atómica de la materia. Sostenía que al desarrollar una teoría se debería ir tan lejos como fuera posible con la termodinámica antes de introducir suposiciones sobre la estructura interna de las sustancias. Se interesó en particular en los problemas de la radiación de cuerpo negro porque creyó que aplicando las leyes tanto de la termodinámica como del electromagnetismo 2 a este sistema se podría llegar a entender cuestiones fundamentales de la física.

En el año de 1889 Planck fue nombrado sucesor de Kirchhoff en la cátedra de física de la Universidad de Berlín. Allí tuvo oportunidad de entrar en contacto cotidiano con los físicos experimentales Rubens y Kurlbaum, que entonces estaban dedicados a medir propiedades de la radiación del cuerpo negro. Planck se dedicó estos años a estudiar procesos irreversibles relacionados con la radiación de cuerpo negro.

La Academia de Ciencias de Berlín había programado una reunión para octubre de 1900 en la que Rubens y Kurlbaum iban a presentar un informe de sus resultados experimentales en el que establecían, sin lugar a dudas, que la distribución de Wien no se ajustaba a la realidad para las frecuencias bajas. Mostraron el informe a Planck unos días antes de la reunión. Planck se convenció de que se tenía que revisar la deducción hecha de la fórmula de Wien.

Planck se metió de lleno a este arduo trabajo. Dados los antecedentes de su trabajo en termodinámica, decidió ver hasta dónde se podía llegar sin hacer suposiciones microscópicas. Para ello utilizó magistralmente la segunda ley de la termodinámica y con ella buscó la forma que debía tener una propiedad termodinámica particular, la entropía. Esta cantidad queda determinada por la distribución de frecuencias. Lo que hizo Planck fue calcular primero la entropía, suponiendo la distribución de Wien y luego volvió a calcular la entropía tomando la distribución de Rayleigh. Naturalmente que las dos formas que encontró eran diferentes. En seguida lo que hizo fue lo que en matemáticas se llama una interpolación; es decir, buscó un puente, por decirlo así, entre estas dos expresiones. Así propuso una expresión que en un extremo se reduce a la correspondiente de Wien, mientras que la misma expresión se reduce, en el otro extremo a la correspondiente de Rayleigh. En la figura 24 se muestra la distribución, a distintas temperaturas, que así obtuvo Planck. En la figura 25 se comparan, a una temperatura fija, las distribuciones de Planck con las de Wien y Rayleigh. Se notará que a bajas frecuencias la distribución de Rayleigh coincide con la de Planck, mientras que a altas frecuencias la de Wien se confunde con la de Planck. A frecuencias intermedias las distribuciones de Rayleigh y de Wien no coinciden con la de Planck.

Planck expuso su resultado en la reunión mencionada de la Academia, como comentario después de la presentación del trabajo de Rubens y Kurlbaum. En la misma noche, Rubens hizo algunos experimentos y confirmó que el acuerdo entre la distribución de Planck y las mediciones que acababa de obtener eran excelentes. Posteriormente Lummer y Prigsheim también verificaron experimentalmente la fórmula de Planck.

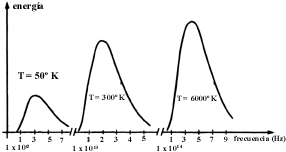
Figura 24. Distribución de Planck para distintas temperaturas. El máximo también se desplaza al aumentar la temperatura. Nótense los cambios de escala para la frecuencia.

Esta interpolación fue una de las contribuciones más significativas e importantes jamás hechas en la historia de la física. Sin embargo, el mismo Planck fue el primero en estar consciente de que la interpolación que había hecho era completamente empírica. No tenía ninguna justificación teórica para su proceder. Lo que sí parecía, que era correcta. En la misma sesión Planck la llamó una feliz adivinanza.

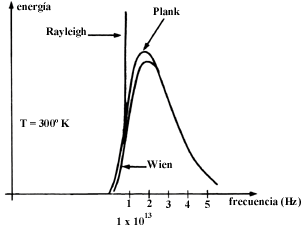
Figura 25. Comparación de las distribuciones de Wien, Rayleigh y Planck a la misma temperatura.

Planck decidió intentar transformar este estado de cosas y poder justificar su interpolación de manera que fuera "una afirmación de significado físico real" como él mismo lo expresó. Para ello no tuvo más remedio que abandonar el manejo termodinámico macroscópico y usar una descripción microscópica de la entropía. Boltzmann ya había trabajado años antes en este tema en el contexto de la teoría cinética, habiendo expresado la entropía en términos de las posibles distribuciones de configuración y de velocidad del sistema compatibles con su energía. Esto último significa lo siguiente. Consideremos un gas de partículas (figura 26 a): supóngase que la partícula 1 tiene una velocidad, digamos v₁; que la partícula 2 tiene una velocidad v₂, etc. Una vez conocidos estos valores de las velocidades, se puede calcular la energía total del gas. Se puede uno imaginar ahora otro gas (figura 26 b) compuesto de las mismas partículas, pero ahora con la partícula 1 teniendo la velocidad v₁, distinta a v₁que tenía la partícula 1 en el primer gas. De la misma forma, ahora la partícula 2 tiene velocidad v'₂, etc. Calculando ahora la energía total de este segundo gas, puede ocurrir que esta energía total sea igual a la energía total del primer gas. Esto quiere decir que cada partícula de un gas tiene una energía distinta a la correspondiente en otro gas, pero la suma de todas las energías da el mismo valor. Decimos que se tienen dos distribuciones microscópicas de las velocidades de las partículas compatibles con el mismo valor de la energía total. Habida cuenta de que el número de partículas en un gas es muy grande (10²⁰ [un uno seguido de veinte ceros] partículas en un centímetro cúbico de gas) es claro que hay un número muy grande de distribuciones distintas todas compatibles con el mismo valor de la energía.

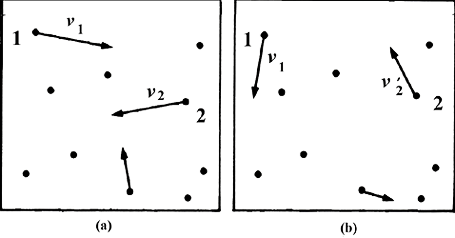
Figura 26. Dos gases pueden tener distintas distribuciones de velocidad, pero la misma energía total.

En general, Boltzmann encontró que la entropía de un sistema está relacionada con el número total de distribuciones microscópicas que puede tener el sistema que sean compatibles con el mismo valor de la energía total. Este es el resultado que Planck se vio forzado a usar.

Planck usó el siguiente modelo para tratar la radiación de cuerpo negro producida por una cavidad. Como consecuencia de la ley de Kirchhoff, la naturaleza de la pared no tiene ninguna relevancia, lo único que se requiere es que esté en equilibrio a una temperatura fija. Por tanto, podría usar como modelo para las paredes de la cavidad el que fuera más conveniente. Planck tomó un caso que ya se había estudiado. Supuso que los radiadores de la pared que producen la radiación de cuerpo negro eran lo que se denomina osciladores armónicos, cuyas propiedades ya se conocían. Supuso que por cada frecuencia que estuviese presente en la radiación había en la pared por lo menos un oscilador de la misma frecuencia. El siguiente paso fue determinar el número de distribuciones posibles de los osciladores de cierta frecuencia compatibles con la energía de la radiación a esa misma frecuencia. Aquí se vio en la necesidad de hacer una suposición. Según la mecánica un oscilador puede tener cualquier valor de su energía, es decir, puede tener una magnitud continua. Pero si se usa esta concepción tradicional no se podría seguir un procedimiento combinatorio para determinar el número de distribuciones totales. Como él mismo lo manifestó:

Ahora tenemos que considerar la distribución de la energía, digamos U, correspondiente a cierta frecuencia entre todos los osciladores que tienen la misma frecuencia. Si U se pudiera considerar como una cantidad divisible infinitamente, la distribución se podría hacer en un número infinito de maneras. Nosotros consideraremos, sin embargo —y este es el punto cardinal de todo el cálculo— a U como si estuviese compuesto de un número finito de partes discretas iguales[...] la energía de cada uno de estos elementos es igual al producto de una constante h por la frecuencia del oscilador.

En consecuencia, Planck se vio forzado a suponer que la energía total era la suma de un número entero de lo que llamó "elementos de energía" o "cuantos de energía" para poder utilizar distintas distribuciones de la energía.

Con las suposiciones anteriores, Planck encontró que la distribución de la radiación de cuerpo negro era efectivamente la que había encontrado empíricamente y que se muestra en la figura 24. Asimismo, comparando sus cálculos con los resultados experimentales de Rubens y colaboradores obtuvo el valor numérico de la constante h.3 A esta constante se le ha llamado la constante de Planck.

Como Planck describió su trabajo al recibir el premio Nobel de Física en 1920: "Después de varias semanas 4 del trabajo más arduo de mi vida, la oscuridad se levantó y un paisaje inesperado empezó a aparecer." En la reunión de la Sociedad Alemana de Física, el 14 de diciembre de 1900, Planck presentó estos resultados bajo el título "Sobre la teoría de la ley de distribución de energía del espectro normal". Es así como nació la mecánica cuántica.

En este momento queremos subrayar algunos puntos. En primer lugar, en ningún lugar de su trabajo Planck destacó la hipótesis que había hecho de que la energía de cada oscilador (o sea de cada partícula que compone a la pared) fuera un múltiplo entero de una energía característica, relacionada con su frecuencia, o sea que la energía solamente se puede dar en "paquetes". Así como se relató arriba, Planck consideró que la "discretización" de la energía era solamente un artificio matemático que se había visto forzado a usar para poder aplicar las ideas de Boltzmann. Recordamos que solamente se puede tener un número finito de distribuciones cuando se tiene un número finito de elementos, en este caso, de "paquetes" de energía. Planck no le adscribió ninguna realidad física a esta cuantización de la energía. Más adelante, en l931, Planck describió en una carta el estado en que se encontraba al hacer la hipótesis de la cuantización: "Fue un acto de desesperación que hice porque se tenía que dar una explicación teórica a toda costa, cualquiera que fuera el precio." Sin embargo, él mismo no estuvo satisfecho, ya que esta suposición era contraria a los principios de la mecánica de Newton en la cual la energía era una cantidad continua; no había forma de que, sin más, fuera discreta.

El físico holandés H. A. Lorentz aclaró que la única consecuencia de la mecánica de Newton era la ley de distribución de Rayleigh, que utilizaba el teorema de equipartición de la energía. Por tanto, la distribución de Planck era contraria a los principios de la mecánica de Newton.

En los años siguientes al trabajo de Planck, prácticamente nadie le puso atención. Se pensó que su hipótesis no tenía mayores consecuencias físicas. De hecho, de manera inconsciente se esperaba que alguien justificara de manera satisfactoria la distribución obtenida, pero en forma congruente con los principios de la mecánica de Newton.

Lo que sí se hizo fue un intenso trabajo experimental para verificar la distribución de Planck en un amplio rango de frecuencias. Así, la distribución de Planck fue confirmada en experimentos realizados por L. Holborn y S. Valentiner hasta temperaturas de 1 600ñC, por W. W. Coblentz para frecuencias altas, por E. Warburg y un grupo de colaboradores en distintas condiciones, etcétera. Todos ellos llegaron a la conclusión de que la distribución obtenida por Planck describía perfectamente bien la realidad.

En vista de la confirmación experimental de las conclusiones del trabajo de Planck, se intentó justificarlo teóricamente sin abandonar la mecánica de Newton. Lorentz admitió: "No podemos decir que al mecanismo de estos fenómenos Planck le ha quitado el velo y debemos admitir que es difícil ver la razón de esta partición de la energía en porciones finitas, que ni siquiera son iguales una a otra, sino que varían de un oscilador a otro, ya que sus frecuencias varían".

NOTAS

1 A la temperatura de 525ñC el platino adquiere una coloración rojiza mientras que a 1 200ñC es completamente blanco.

2 Para la época en que Planck trabajaba ya se había establecido que la luz era una parte de las ondas electromagnéticas.

3 El valor de la constante de Plank es 6.63 x 10^-34 joule seg.

4 Fueron 8 semanas.