X. EINSTEIN DA LA LUZ AL ENIGMA DE LOS CALORES ESPECÍFICOS

INCLUSO después de la publicación del trabajo de Einstein sobre el efecto fotoeléctrico, en 1905, la situación de la teoría de Planck se podía considerar, desde el punto de vista macroscópico, como el resultado de una interpolación matemática y desde el punto de vista microscópico como el de una suposición matemática de que las energías que podía absorber o emitir una partícula en interacción con la radiación electromagnética tenían que ser unidades discretas, llamados "cuantos" de energía. Para Planck éste fue un simple artificio para poder llegar al mismo resultado que el obtenido por su interpolación.

En el trabajo de 1905, Einstein argumentó por primera vez sobre la realidad física de la cuantización de la energía de la radiación electromagnética. Como vimos en el capítulo anterior, con ello pudo explicar varios fenómenos que parecían contradictorios con las ideas que entonces se tenían. Sin embargo, esta aplicación, por muy importante que fuese, seguía estando dentro del dominio de la radiación electromagnética.

Hasta este momento el resto de la comunidad científica consideraba que los trabajos de Planck y de Einstein eran ad-hoc, es decir, construidos solamente para explicar la interacción de la radiación electromagnética con la materia y que no eran relevantes ni importantes para otros fenómenos físicos.

Aquí cabe ahora un comentario de mucha importancia. Una teoría física es significativa si, además de explicar los fenómenos físicos para los que ha sido construida, puede también explicar otros fenómenos fuera de su dominio original. En 1907, Einstein publicó un trabajo titulado "La teoría de la radiación de Planck y la teoría de los calores específicos", con el que dio a la teoría de Planck relevancia física en el sentido acabado de mencionar, y de hecho abrió las compuertas de la teoría cuántica. En este trabajo, Einstein aplicó los conceptos cuánticos, que él mismo había utilizado para la radiación electromagnética, a fenómenos termodinámicos en sistemas materiales que no incluían radiación electromagnética. Es así como mostró que las ideas de la cuantización, aplicadas fuera del área de la radiación, podían resolver inconsistencias y paradojas que se presentaban en el área de la teoría cinética, por ejemplo en el caso de los calores específicos de diversas sustancias como los sólidos a bajas temperaturas.

Como se vio en secciones anteriores, la teoría cinética desarrollada por Maxwell, basada en la mecánica de Newton, predecía resultados que contradecían las mediciones experimentales para el calor específico. En efecto, la teoría cinética predecía el teorema de la equipartición de la energía, con el que se concluía que el calor específico de una sustancia, por cada grado de libertad, debería ser una cantidad constante al variar la temperatura. A temperaturas suficientemente altas, esto era lo que efectivamente sucedía, y queda englobado en la ley de Dulong-Petit. Sin embargo, al disminuir la temperatura de las sustancias y medir sus calores específicos se encontraron dos cosas: a) que el calor específico variaba al cambiar la temperatura y b) al disminuir la temperatura el calor específico disminuía, de tal suerte que al acercarse al cero absoluto (es decir a 273ºC bajo cero) el calor específico tendía a anularse.

La teoría cinética entonces conocida no podía explicar estos resultados.

Refiriéndose a la hipótesis de Planck de que durante el proceso de absorción o emisión de energía en la radiación, los valores de la energía solamente podían variar en múltiplos del producto de la constante de Planck h multiplicada por la frecuencia del oscilador, Einstein mencionó lo siguiente en su trabajo de 1907:

No deberíamos estar satisfechos, yo creo, con esta conclusión ya que la siguiente cuestión llega a nuestra mente: si es que efectivamente es cierto que las oscilaciones elementales que se usan en la teoría de la transferencia de energía entre radiación electromagnética y la materia no se pueden interpretar en términos de la teoría cinética molecular que actualmente conocemos, ¿no deberíamos también modificar nuestra teoría para otras oscilaciones que se usan en la teoría del calor? En mi opinión no hay duda sobre la respuesta. Si la teoría de Planck realmente llega a la esencia de este asunto, entonces uno debería esperar que las contradicciones que existen en otras áreas de la teoría del calor entre la teoría cinética molecular actual y la experiencia, pudieran ser resueltas por medio del método acabado de proponer.

Las otras oscilaciones a las que Einstein se refiere son las siguientes. En los modelos de sólidos se supone que las moléculas que los componen se encuentran localizadas en ciertos puntos del espacio distribuidos en forma regular, formando un cristal (figura 4). Estos puntos se llaman los puntos de la red o malla cristalina. Las partículas que componen el cristal pueden oscilar alrededor de estos puntos de la red, con amplitudes muy pequeñas. Es claro que si las amplitudes son grandes, entonces ya no tiene mucho sentido hablar de partículas localizadas y, por lo tanto, de un cristal.

Einstein demostró en su trabajo que la disminución del valor del calor específico de los sólidos al disminuir la temperatura podía explicarse tomando como base las ideas cuánticas de Planck. Para simplificar su tratamiento matemático, supuso que todos los átomos del sólido oscilaban con la misma frecuencia y encontró entonces una expresión para su calor específico cuya gráfica como función de la temperatura se muestra en figura 30. Las características de este resultado son:

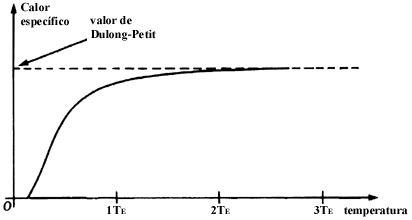
Figura 30. Comportamiento del calor específico de un sólido, obtenido por Einstein basado en la hipótesis cuántica.

a) Para altas temperaturas (véase punto b), el calor específico adquiere el valor dado por la ley de Dulong -Petit.

b) Einstein encontró que existe una temperatura característica T_E del sólido, relacionada con la frecuencia con que oscilan las partículas. Es con respecto a este valor que se puede hablar de altas o bajas temperaturas. Así, altas temperaturas significan valores de la temperatura mucho mayores que la temperatura característica T_E.

c) Al disminuir el valor de la temperatura y acercarse al de la temperatura característica T_E el calor específico del sólido cambia con la temperatura. De hecho disminuye, como puede verse experimentalmente.

d )Al acercarse al cero absoluto de la temperatura, el valor del calor específico se hace cada vez más y más pequeño. Einstein encontró que en el cero absoluto, el calor específico se anula.

De esta manera Einstein explicó que el hecho de que el calor específico de una sustancia varíe el cambiar su temperatura ¡es una manifestación macroscópica de efectos cuánticos!

Comparando las figuras 5 y 30 vemos que hay concordancia cualitativa entre la predicción de Einstein y los valores experimentales para el calor específico. Sin embargo, al hacer una comparación cuantitativa detallada, se encuentra que a bajas temperaturas no hay concordancia. Einstein predijo que el valor del calor específico debe disminuir mucho más rápidamente de lo que en realidad lo hace. De hecho, hablando en lenguaje matemático, Einstein predijo una disminución exponencial, mientras que experimentalmente la disminución va como la temperatura absoluta T elevada a la tercera potencia, la llamada ley T³.

Es claro que uno no debería esperar de un modelo tan simplificado como el de Einstein una concordancia cuantitativa. En los sólidos reales no todas sus partículas oscilan con la misma frecuencia. En realidad hay un número muy grande de frecuencias distintas, es decir, hay una distribución de frecuencias. Sin embargo, esto no es lo importante en este momento, sino el hecho de poder extraer la conclusión de que los efectos cuánticos son los responsables de la disminución del valor del calor específico. Aquí también Einstein demostró su genio especial, al poder diseñar modelos lo suficientemente sencillos para poder hacer conclusiones fundamentales. Más adelante, en 1912, Peter Debye refinó este modelo de Einstein tomando en cuenta justamente el hecho de que las frecuencias con las que vibran las partículas de un cristal son muchísimas y pudo predecir que a bajas temperaturas el comportamiento es como T³, todo basado en las ideas cuánticas de Einstein.