XII. LAS SIGUIENTES ETAPAS DE LA HISTORIA

AL FINALIZAR el primer Congreso Solvay, en 1911, termina la etapa inicial de la historia de la teoría cuántica, en la que gran parte de la comunidad científica ha reconocido que en la suposición de Planck hay "algo" real. Fueron los trabajos de Einstein ya mencionados donde por primera vez se aplicaron estas ideas. Los modelos en que se usaron estas ideas fueron esencialmente de osciladores armónicos. Las ideas cuánticas no se habían aplicado a otro tipo de sistemas, ni se sabía cómo hacerlo. Sin embargo, las aplicaciones hechas fueron suficientes para concluir que la física clásica era limitada. El problema entonces sería cómo desarrollar una teoría consistente.

En 1913 se inicia la segunda etapa del desarrollo de la física cuántica, al publicar Niels Bohr su notable trabajo Sobre la constitución de átomos y moléculas, en el cual aplicó las ideas cuánticas a la estructura del átomo de hidrógeno. Para apreciar esta contribución haremos un breve paréntesis.

En 1666 Newton inició el estudio de la luz por medios espectroscópicos al hacer incidir un haz luminoso sobre un prisma y descubrir que, debido a la refracción, se separaban las componentes de las que estaba formado el haz (figura 8). En particular, descubrió de esta manera que la luz blanca que nos llega del Sol está compuesta por todos los colores, formando un continuo. Esto significa que al fijarnos en los colores que salen del prisma, se pasa de un color a otro de manera continua, imperceptible. Esta descomposición nos es familiar, pues basta recordar el arco iris que forma no un prisma sino las gotas de agua de la lluvia.

Posteriormente se aplicó este método para estudiar la luz que emiten diversas sustancias. Esto se hizo calentándolas y haciendo incidir la luz que emiten sobre un espectroscopio. Éste es un aparato (figura 31) que tiene un prisma para analizar la luz. De esta forma se descubrió que la luz que emiten las sustancias no está formada, en general, por un continuo de colores, sino que solamente están presentes ciertos colores. Por ejemplo, en los gases sólo se observan rayas o líneas de ciertos colores. A este conjunto de colores se le llama el espectro de la sustancia. Así, en la figura 32 se muestran algunos espectros de gases como neón, mercurio, sodio. Cada una de estas líneas tiene un color bien preciso. Por ejemplo, la línea del sodio es amarilla. Empíricamente se pudieron encontrar las frecuencias de las líneas que aparecían en los espectros de muchas sustancias, en particular de elementos químicos. Es importante mencionar que los espectros son característicos de cada sustancia. Como se ve en la figura 32, distintas sustancias tienen espectros distintos. De hecho, el espectro ha servido para identificar sustancias, utilizando algo así como su huella digital. De este modo, estudiando espectroscópicamente la luz que llega de los planetas, las estrellas y demás cuerpos estelares se ha podido determinar de qué sustancias están compuestos.

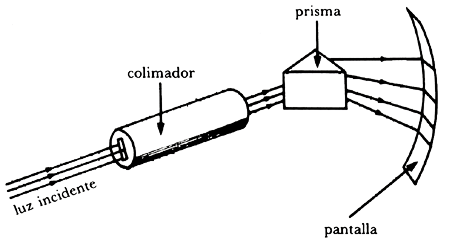
Figura 31. Esquema de un espectroscopio que se usa para analizar las componentes de un haz de luz emitido por cualquier sustancia.

Figura 32. Espectros del neón, mercurio y sodio obtenidos con un espectroscopio. Cada línea corresponde a un color (frecuencia) bien determinado. La línea marcada del sodio tiene color amarillo.

Hacia fines del siglo pasado ya se habían estudiado con mucho detalle los espectros de muchas sustancias. Se pudo determinar también que eran las partículas que forman a los cuerpos las que emiten las líneas característica del espectro. Se creyó que las diferencias entre los espectros y la complejidad de algunos de ellos (en algunos espectros hay miles de líneas) tenía algo que ver con la estructura de las partículas mismas. Se presentaba la cuestión de cuáles eran los procesos por medio de los cuales las partículas que componen un cuerpo reciben energía (por ejemplo, del calentamiento) y la emiten en forma de luz (o más bien, de ondas electromagnéticas) de frecuencias bien definidas. Al aplicar la física clásica no se había podido explicar la causa de que los espectros fueran discretos.

Por otro lado, hacia finales del siglo pasado se habían empezado a formular los primeros modelos de la estructura de los átomos. Sin entrar en detalles, solamente mencionaremos que de todas las propuestas la que resultó relevante fue la hecha por Ernest Rutherford. En 1911 presentó un trabajo que resultó clásico La dispersión de partículas a y b por materia y la estructura del átomo, en el que mostró una serie de resultados de sus experimentos en los que concluía que el átomo debería tener una estructura análoga al sistema planetario solar, esto es, formado por un núcleo de carga eléctrica positiva, de mucha masa, en su centro y a su alrededor un conjunto de electrones, de carga eléctrica negativa, girando alrededor del núcleo (figura 33). Posterior a su publicación, este modelo fue verificado en diversas situaciones con el resultado de que era satisfactorio.

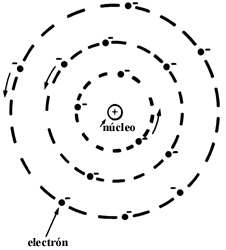
Figura 33. Modelo del átomo sugerido por Rutherford como consecuencia de sus experimentos.

En 1912, Niels Bohr se unió al grupo de Rutherford en Manchester, Inglaterra. Bohr llegó justo en un momento importante, cuando se investigaban las consecuencias del modelo atómico de Rutherford. Un problema al que de inmediato se dedicó Bohr fue el de la estabilidad del átomo propuesto. Como es natural, lo primero que hizo fue aplicar la física clásica a esta cuestión, dándose cuenta de que se llegaba a una inmensa contradicción; se dio cuenta de que la estabilidad del átomo, según el modelo de Rutherford, no podía reconciliarse con los fundamentos de la mecánica de Newton y el electromagnetismo de Maxwell.

La teoría electromagnética desarrollada por Maxwell requiere que si una partícula con carga eléctrica, como el electrón, se acelera, tiene que radiar energía electromagnética. En particular, un electrón girando alrededor de un núcleo se acelera, pues se trata de un movimiento que no es uniforme rectilíneo. Dado que las dimensiones de la órbita que recorre el electrón alrededor del núcleo dependen de la energía que tenga —y que al radiar energía la va perdiendo—, como consecuencia las dimensiones de la órbita tienen que disminuir. Según esto el electrón debería seguir una trayectoria en espiral (figura 34).

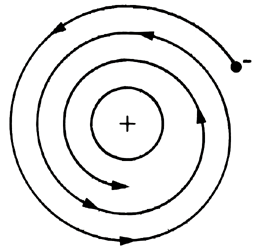
Figura 34. Según la mecánica clásica, un electrón en un átomo debe seguir una trayectoria espiral. Por tanto, este átomo no es estable, contrario a la experiencia.

Esto tiene dos consecuencias. La primera es que la radiación así emitida, según la teoría clásica, debe ser de frecuencias continuas; por lo tanto el espectro de tal átomo debería ser continuo. En segundo lugar, después de cierto tiempo, la órbita del electrón será tan pequeña que chocaría con el núcleo y, por tanto, desaparecería el átomo. Es decir, al aplicar la física clásica al modelo de Rutherford predice que ñla materia no es estable!. Como dijo Bohr en su trabajo:

El electrón se acercará al núcleo, describiendo órbitas de dimensiones menores y menores y girará con frecuencias mayores y mayores [...]. El proceso continuará hasta que las dimensiones de la órbita sean del mismo orden de magnitud que las dimensiones del electrón o las del núcleo. Un cálculo sencillo muestra que la energía radiada durante el proceso considerado será enormemente grande comparada con la radiada durante los procesos moleculares ordinarios. Es obvio que el comportamiento de tal sistema será muy distinto al de un sistema atómico que ocurre en la naturaleza. En primer lugar los átomos reales en su estado permanente parecen tener dimensiones y frecuencias absolutamente fijas. Además, si consideramos cualquier proceso molecular, los resultados siempre parecen ser que, después de que cierta cantidad de energía característica del sistema en cuestión es radiada, el sistema se acomodará otra vez en un estado de equilibrio estable, en el cual las distancias entre las partículas son del mismo orden de magnitud que tenían antes del proceso. Sin embargo, la forma de considerar un problema de este tipo ha experimentado alteraciones esenciales en los últimos años debido al desarrollo de la [teoría cuántica de la] radiación electromagnética, y la afirmación directa de las nuevas suposiciones introducidas en esta teoría, encontrada por experimentos en muy diversos fenómenos tales como calores específicos, efecto fotoeléctrico. El resultado de la discusión de estas cuestiones parece ser el acuerdo general de que el electromagnetismo clásico es inadecuado para describir el comportamiento de sistemas de tamaños atómicos. Cualquiera que sea la alteración en las leyes de movimiento de los electrones, parece ser necesario introducir en las leyes en cuestión una cantidad extraña al electromagnetismo clásico, es decir, la constante de Planck. Introduciendo esta cantidad, la cuestión de la configuración estable de los electrones en los átomos cambia esencialmente.

Motivado por lo anterior, Bohr sugirió una aplicación directa de la hipótesis del fotón de Einstein como sigue:

a) Abandonar la teoría electromagnética clásica en la medida de suponer que, en órdenes de magnitudes atómicas, los electrones pueden girar en órbitas estables sin radiar continuamente energía en forma de ondas electromagnéticas, como lo requeriría la teoría clásica. Así, la energía de un electrón depende de las dimensiones de su órbita. Al pasar el electrón de una órbita estable a otra, y en vista de que estas órbitas tienen dimensiones distintas, entonces el electrón tendrá otra energía. De esta manera el electrón cambia de energía solamente al transferirse de una órbita a otra. Mientras permanezca en su órbita el electrón tendrá la misma energía. Dependiendo de si la órbita final tiene un tamaño mayor o menor, el electrón absorberá o emitirá energía, es decir, radiará ondas electromagnéticas. Aquí Bohr, de hecho, supuso la existencia de un conjunto discreto de órbitas estacionarias.

b) En seguida, Bohr usa el modelo de Einstein. La energía absorbida o emitida por un electrón al cambiar de órbita está asociada con la absorción o emisión de fotones individuales o cuantos de energía. La frecuencia de estos fotones multiplicada por la constante de Planck, o sea su energía, es igual a la diferencia de energía del electrón al pasar de una órbita a otra. Esto quiere decir que el cambio de energía que experimenta el electrón es justamente la energía del fotón absorbido o emitido. En particular, si un electrón pasa de una órbita grande a otra pequeña (figura 35) disminuye su energía, por lo que emite un fotón que tiene justamente esta energía, y por tanto una frecuencia bien determinada.

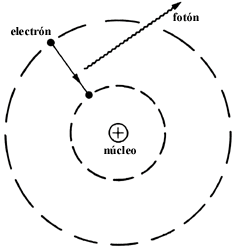
Figura 35. Según Bohr, un electrón al pasar de una órbita grande a una más pequeña emite un fotón.

c) Para proceder en la aplicación de la cuantización, Bohr hizo lo siguiente. Se dio cuenta que la constante de Planck era una cantidad que tenía las mismas dimensiones que otra con la que se trabaja mucho en mecánica, a saber, el momento angular. Hizo la suposición de que el momento angular del electrón solamente puede tener valores iguales a múltiplos de la constante de Planck.

Bohr trabajó con el átomo más sencillo posible, el de hidrógeno, ya que solamente tiene un electrón. Con las suposiciones anteriores Bohr encontró los valores de las frecuencias que debería tener la radiación emitida por el electrón. Resultó que estos valores que obtuvo concordaban, en un buen grado de precisión, con los valores experimentales que ya se conocían desde hacía mucho tiempo. Además, encontró, en términos de la masa del electrón, de las cargas eléctricas del electrón y del núcleo y de la constante de Planck, una cantidad que se había obtenido empíricamente, en relación a los espectros de los átomos, que es la llamada constante de Rydberg. Asimismo, Bohr predijo la existencia de otras líneas del espectro que no caían en la región visible, sino en el ultravioleta extremo y en el infrarrojo extremo. Parte de estas predicciones fueron verificadas experimentalmente por T. Lyman en 1914, otra parte por F. Brackett en 1922 y otra parte más por A. H. Pfund en 1924.

El trabajo de Bohr fue recibido, en general, en forma favorable. Einstein se dio cuenta de la importancia de este trabajo. Se refirió a él como un "logro enorme" y como "uno de los más grandes descubrimientos". En esa época Einstein trabajaba en Zurich, donde semanalmente se llevaba a cabo un coloquio de física. En uno de los coloquios se presentó la teoría de Bohr. Al final de la discusión el notable físico Max von Laue explotó: "Son tonterías. La teoría de Maxwell es válida en todas las circunstancias." A lo que Einstein contestó: "Muy notable. Debe haber algo atrás de esto. No creo que la derivación del valor de la constante de Rydberg sea puramente fortuita.''

En Inglaterra el trabajo de Bohr causó sensación. Así el físico James Jeans declaró "los resultados obtenidos son muy notables para descartarlos como puramente accidentales". The Times publicó una nota con el encabezado "La ingeniosa explicación del Dr. Bohr del espectro del hidrógeno".

A pesar del gran éxito que obtuvo Bohr con el átomo de hidrógeno, al intentar extender la teoría a otros átomos aparecieron dificultades importantes. En los años siguientes fueron Planck (ya más convencido de que la teoría cuántica tenía realidad física) y Arnold Sommerfeld quienes estuvieron muy activos en el desarrollo de la teoría.

Arnold Sommerfeld generalizó la aplicación de las condiciones de cuantización para casos más complicados. En particular, usó la condición de la cuantización del momento angular no con la mecánica de Newton como lo había hecho Bohr sino con la mecánica relativista que había desarrollado Einstein. En 1916 encontró que cada una de las líneas que había obtenido Bohr se dividía en varias líneas muy cercanas entre sí (figura 36). Este efecto, llamado de estructura fina, ya lo había descubierto A. Michelson en 1891 al medir con muchísima precisión las líneas espectrales del hidrógeno y debe añadirse que es extremadamente pequeño y que durante mucho tiempo no fue tomado en cuenta por los científicos. Posteriormente, F. Paschen lo midió con muy alta precisión en el espectro del helio ionizado 1 obteniendo una extraordinaria concordancia cuantitativa con la predicción de Sommerfeld.

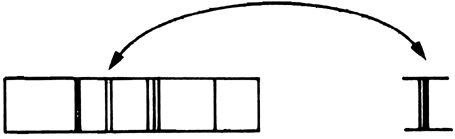
Figura 36. Al analizar muy detenidamente cada línea del espectro, resulta que está formada por varias líneas muy juntas entre sí.

Con base en la generalización de Sommerfeld, se desarrolló todo un cuerpo de teoría sobre la estructura atómica y los espectros correspondientes.

Por otro lado, en 1916, después de haber terminado de formular la teoría de la relatividad general, Einstein volvió a tomar el problema de la radiación electromagnética y derivó de una manera más general la distribución que Planck había obtenido en 1900. Para ello analizó con detenimiento el mecanismo de las transiciones que ocurren al pasar el electrón de una órbita a otra, o sea de un estado a otro. Einstein hizo la suposición de que estas transiciones están gobernadas por una probabilidad de ocurrencia. Para encontrar la distribución consideró primero la probabilidad de la absorción de un fotón al pasar un electrón de un estado de baja energía a otro de mayor energía. Naturalmente, el átomo absorbe esta energía de la radiación presente en la que se encuentra. Además, consideró la probabilidad de que un electrón pase de un estado de energía alta a otro de energía más baja. De esta manera emite un fotón. Sin embargo, para poder llegar a la distribución de Planck, Einstein descubrió que la emisión puede ocurrir por medio de dos mecanismos distintos: uno es la emisión espontánea, proceso que se da al estar el electrón en un estado de alta energía y, sin que medie factor externo o conocido alguno, de pronto emite un fotón y el electrón pasa a un estado de energía más baja. Este proceso de emisión ocurre aun cuando el átomo no se encuentre en presencia de radiación. Este mecanismo es el que se esperaría que ocurriera, ya que, en general, un sistema tiende a alcanzar, espontáneamente, su estado de energía más bajo. Sin embargo, Einstein descubrió que es necesario que también ocurra otro proceso de emisión, que él denominó emisión inducida o estimulada. Esto significa que, en presencia de radiación, este campo externo estimula al átomo a que el electrón pase de un estado de alta energía a otro de baja energía. En la teoría electromagnética clásica no se da este último proceso. Es tomando en cuenta también el proceso de emisión estimulada que Einstein obtuvo la distribución de Planck. Si no se tomara en cuenta este nuevo mecanismo se obtendría la distribución de Wien. Es importante mencionar que es precisamente este último mecanismo el que se utiliza en el láser. 2

Una cosa muy importante ocurrió con este trabajo de Einstein. En él no se preocupó de dilucidar las causas detalladas de las transiciones, motivo por el cual usó probabilidades. Einstein afirmó que un átomo podría pasar de un estado a otro de energía más baja "sin excitación por una causa externa", afirmación que Bohr interpretó y posteriormente usó como un proceso sin causa. De esta manera, por primera vez se habló en la física cuántica de procesos acausales, a los que solamente se les asigna una probabilidad de ocurrencia. Más adelante hablaremos más sobre este asunto.

Aunque las ideas cuánticas, y en particular la teoría de Bohr acerca de la estructura atómica, tuvieron muchos triunfos, al transcurrir el tiempo, a principios de la década de 1920, cada vez era más claro que la teoría conocida no era la adecuada. Por un lado existía todavía un buen número de fenómenos que no se habían podido explicar porque no se sabía como cuantizar" su descripción y en algunos casos en que sí se había cuantizado, los resultados obtenidos no concordaban completamente con las mediciones experimentales.

Por otro lado, un vistazo a lo que se había desarrollado hasta ese entonces mostraba que la manera en que se habían obtenido los resultados era muy poco satisfactoria. En efecto, lo que se había hecho en gran medida era modificar, sin justificación básica, de manera ad-hoc, algunos de los principios de la mecánica de Newton y del electromagnetismo de Maxwell y añadir artificialmente condiciones de cuantización. En esencia, lo que se tenía era una doctrina inconsistente en lo interno. Ya en 1901 Einstein había llamado la atención sobre esta situación. En el caso de la derivación que había hecho Planck de la distribución de radiación de cuerpo negro, comentó que había una inconsistencia lógica ya que se trabajaba en algo basado en un simultáneo rechazo y aceptación del electromagnetismo clásico. Lo que se necesitaba era una física cuántica racional y autoconsistente que partiera de fundamentos lógicos bien claros. Esto se descubrió en 1926. No entraremos en los detalles del desarrollo de esta formidable teoría, sino que solamente haremos algunos breves comentarios.

En noviembre de 1924, Louis de Broglie presentó en la Universidad de París su tesis doctoral "Investigaciones sobre la teoría de los cuanta". Al llevar a cabo este trabajo, De Broglie estuvo muy influenciado, entre otras cosas, por el trabajo de Einstein de 1905 sobre los cuantos de radiación (fotones) así como por algunas ideas de su teoría de la relatividad especial. Hasta ese momento se había aceptado, aunque no entendido muy bien, el carácter dual de la radiación: en ciertas circunstancias la luz se comportaba como onda y en otras, como partícula. L. de Broglie avanzó un paso al llegar a la idea de que, al igual que la luz, la materia también debería tener este comportamiento dual. Desarrolló la teoría en la que estableció el paralelismo entre el movimiento de una partícula y la propagación de la onda con la que está asociado. Al final de su tesis dice: "La presente teoría debe ser considerada como un esquema formal cuyo contenido físico no está aún completamente determinado." El jurado examinador reconoció la originalidad del trabajo, pero no creyó en la realidad física de las ondas acabadas de proponer. Al preguntarle uno de los miembros del jurado, Jean Perrin, si la existencia de estas ondas se podría verificar experimentalmente, De Broglie contestó que esto debería ser posible por medio de experimentos de difracción por cristales. Se recordará que el fenómeno de difracción está asociado al carácter ondulatorio de lo que se difracta. De hecho, De Broglie había propuesto hacer un experimento al respecto a Alexandre Dauvillier, uno de los colaboradores de su hermano Maurice, pero estaba muy ocupado experimentando con televisión.

En el verano de 1924, Einstein recibió una carta, acompañando un trabajo en inglés, de Sayandra Nath Bose de la Universidad de Dacca en la India que empezaba así:

Respetado señor, me he atrevido a enviarle el artículo que se acompaña para su lectura y opinión. Estoy ansioso de saber lo que Ud. piensa de él. Podrá apreciar que traté de encontrar la ley de Planck independientemente de la electrodinámica clásica. No sé suficiente alemán para traducir el trabajo. Si Ud. cree que el trabajo amerita su publicación le estaré agradecido si pudiera disponer su publicación en el Zeitschrift fñr Physik. Aunque soy un completo extraño para Ud. no vacilo en hacerle tal petición, porque todos somos sus discípulos aunque beneficiándonos de sus enseñanzas solamente a través de sus escritos.

Einstein reconoció inmediatamente la importancia del trabajo, lo tradujo al alemán y lo envió a su publicación, que apareció ese mismo año.

Sin embargo, Einstein hizo más que eso. Aplicó el enfoque de Bose a un gas compuesto de partículas monoatómicas y encontró que se podía establecer "una relación formal de gran alcance entre radiación y gas". Einstein calculó otra vez, al igual que lo había hecho en 1909, pero ahora para el gas de partículas, las fluctuaciones en los valores de la energía, con respecto a su promedio. Volvió a encontrar (véase el capítulo IX) que estas fluctuaciones están compuestas de la suma de dos términos: uno que corresponde al que se obtendría de la teoría cinética de Maxwell-Boltzmann para partículas y el otro, que se obtendría con base en una teoría ondulatoria. Es decir, Einstein encontró que en las partículas materiales también se da una dualidad análoga a la que se presenta en el caso de la radiación electromagnética. Einstein publicó este trabajo en septiembre de 1924.

Louis de Broglie le envió una copia de su tesis a Einstein. Posteriormente, en febrero de 1925, Einstein publicó un trabajo más sobre esta cuestión en la que discutió esta interpretación de la dualidad partícula-onda en la materia con mayor detalle ya que "creo que involucra más que una mera analogía".

En 1927, C. J. Davisson y L. H. Germer en Estados Unidos por un lado y G. P. Thomson en Inglaterra por el otro demostraron experimentalmente que un haz de electrones que se hace incidir sobre un cristal se difracta. Aquí el cristal desempeña el papel de rejilla de difracción. Esta fue una confirmación experimental de que efectivamente los electrones, que se habían considerado como partículas, también tienen un comportamiento ondulatorio. En una reunión científica en 1928 Davisson dijo: "Durante los últimos años hemos llegado a reconocer que hay circunstancias en las cuales es conveniente, si no es que necesario, considerar a los electrones como ondas, más que partículas, y cada vez más y más frecuentemente hacemos uso de términos tales como difracción, refracción, reflexión y dispersión en la descripción de su comportamiento."

En 1929 se otorgó el premio Nobel de Física a De Broglie y posteriormente, en 1937 lo recibieron Davisson y Thomson.3

En 1925 Werner Heisenberg publicó un trabajo con el que se inició un nuevo enfoque de la física cuántica. Aquí Heisenberg tomó la posición de dejar de utilizar los términos con los que se hacía la descripción de los sistemas atómicos (o para el caso, de los sistemas microscópicos) en la física clásica. En particular, insistió en usar solamente cantidades que pudieran ser observables. Es así que rechazó las nociones clásicas de posición, velocidad, órbita, etcétera de un electrón en un átomo ya que nadie las había medido directamente. Se basó en dos consideraciones empíricas para tomar este paso: la imposibilidad experimental de medir dichas cantidades directamente y el fracaso práctico de una teoría (la clásica) que las suponía observables. Entonces, ¿con qué cantidades se va a hacer la descripción? Propuso usar cantidades como frecuencias, intensidades de radiación, etcétera, que sí son observables. Heisenberg desarrolló así una teoría completamente consistente, en la que tuvo que usar cantidades matemáticas llamadas matrices. Por ello se le llamó la teoría matricial de la mecánica cuántica.

A este trabajo siguieron varios más, en colaboración con Max Born y Pascual Jordan, que constituyen la primera exposición completa de los fundamentos de la mecánica cuántica moderna en su formulación matricial.

Por otro lado, Erwin Schrñdinger, basado en el trabajo de De Broglie sobre las ondas materiales, desarrolló en 1926 una teoría en la que obtuvo la famosa ecuación, que lleva su nombre. Así es como desarrolló lo que se llama la teoría ondulatoria de la mecánica cuántica.

A primera vista las dos teorías así desarrolladas parecerían ser dos cosas distintas. En el mismo año de 1926, Carl Eckart demostró que ambas teorías eran, en efecto, equivalentes. Más adelante Wolfgang Pauli demostró la equivalencia matemática entre las dos teorías. Así, resulta que ambos trabajos son formulaciones distintas de la misma cosa.

Una característica de esta teoría es que indica cómo aplicarla sistemáticamente a distintas situaciones físicas. Ésta es una de las cosas que faltaban en las formulaciones anteriores.

Esta nueva teoría se aplicó, en sus dos formulaciones, a distintos sistemas físicos. En particular, al aplicarla al átomo de hidrógeno resultó que en forma automática se obtienen como consecuencia de la teoría los resultados que había obtenido Bohr en 1913 en forma muy artificial. En general, con esta nueva teoría cuántica, bien fundamentada ahora, se recuperaron los resultados que antes se habían obtenido como parches a la mecánica clásica. Además, con esta teoría se pudieron resolver muchas cuestiones que habían quedado pendientes. En el transcurso de los años se ha aplicado esta teoría a un sinnúmero de situaciones encontrando resultados que al compararse con mediciones experimentales han sido satisfactorios.

Asimismo, se pudo demostrar que en ciertas condiciones, por ejemplo, para sistemas macroscópicos como el movimiento de la Tierra alrededor del Sol, la descripción hecha con la mecánica cuántica coincide con la descripción hecha con ayuda de la mecánica de Newton. Desde este punto de vista, se puede considerar a la teoría clásica como un caso particular al que se reduce la teoría cuántica en situaciones bien definidas. Para otros casos, fuera de los anteriores, la descripción que se ajusta a la realidad es la cuántica.

En lo que respecta al problema con el que iniciamos este libro, a saber, el del calor específico, hay que mencionar lo siguiente. Una vez establecida la nueva mecánica cuántica, se desarrolló la mecánica estadística cuántica con la que se fundamenta la termodinámica, generalizando a los dominios microscópicos la teoría cinética. Se ha podido predecir diversas propiedades termodinámicas de las sustancias, entre ellas el calor específico. Para éste se obtienen expresiones que efectivamente concuerdan con las obtenidas experimentalmente, es decir, con las mostradas en la figura 5. Esto es, concuerdan esencialmente con la predicción de Einstein. El hecho de que el calor específico cambia de valor al cambiar la temperatura de la sustancia es una manifestación cuántica. Además, se pudo explicar satisfactoriamente, en términos de ideas cuánticas, el comportamiento del calor específico para sustancias formadas de moléculas poliatómicas.

Por otro lado, se presentó un importante problema, digamos filosófico, en el que Einstein se vio involucrado, y que corresponde a la interpretación de varios resultados obtenidos como consecuencia de la teoría. No entraremos en el análisis profundo de esta cuestión. Solamente diremos una breves palabras. Una consecuencia obtenida por Heisenberg de la nueva mecánica cuántica fue su famoso principio de incertidumbre, el cual nos dice que si en un experimento uno mide con precisión, la posición de una partícula por ejemplo, entonces no se puede, en principio, determinar al mismo tiempo con precisión su velocidad y viceversa. Esto claramente va contra las ideas clásicas que se tenían de que era posible, por lo menos en principio, determinar simultáneamente todas las cantidades dinámicas asociadas al movimiento de una partícula. Es más, se concluyó que la teoría cuántica tiene carácter estadístico y no determinista como la teoría clásica. Esta interpretación fue trabajada por Max Born, Bohr y muchos otros, y llegó a conocerse como la interpretación de Copenhague, ya que el instituto de Bohr se había vuelto, de hecho, un lugar de reunión de la gente que trabajaba en la frontera de la física, y allí se dilucidó en muchos aspectos esta interpretación.

En consecuencia, la conclusión que se obtuvo fue de que la nueva teoría cuántica era no-determinista. Lo más que se podría obtener era una probabilidad de ocurrencia de alguna situación física. Así se pierde de la descripción de los fenómenos naturales, en principio, la noción de determinismo.

Einstein no estuvo de acuerdo con estas nociones. En 1926 escribió una carta a Paul Ehrenfest en la que decía:" Veo a la nueva mecánica cuántica con admiración y con sospecha." En particular, al leer el trabajo de Heisenberg sobre el principio de incertidumbre intentó demostrar que no era correcto por medio de contraejemplos.

En 1927 se convocó al quinto Congreso Solvay en Bruselas, donde estarían presentes los principales físicos de la época. Einstein pensó que era una buena oportunidad para intercambiar opiniones sobre esta cuestión y posiblemente llegar a una conclusión final. En su presentación, Born y Heisenberg declararon:

La nueva mecánica cuántica nos lleva a resultados precisos con respecto a valores promedio, pero no da información sobre los detalles de actos individuales. El determinismo que hasta ahora se ha considerado como la base de las ciencias exactas debe desecharse. Cada avance adicional de nuestro entendimiento de las fórmulas ha mostrado que una interpretación consistente del formalismo de la mecánica cuántica es posible solamente bajo la suposición de un indeterminismo fundamental. El principio de incertidumbre constituye un indeterminismo inherente en las leyes de la naturaleza debido a la dualidad partícula-onda. Mantenemos que la mecánica cuántica es una teoría completa; sus bases físicas y sus hipótesis matemáticas no son susceptibles de modificaciones adicionales.

Lo notable del Congreso no residió tanto en los trabajos presentados, sino en las discusiones tanto formales como informales, principalmente entre Einstein y Bohr. Einstein expresó su oposición al rechazo del principio de la descripción determinista de la ciencia, y retó a Bohr con "experimentos pensados" muy ingeniosos, con los que trató de mostrar que sí era posible el determinismo. Estas discusiones se volvieron famosas. Einstein proponía uno de estos experimentos y, después de pensarlo, Bohr refutaba el argumento indicando una falacia en el tren de ideas de Einstein. Este debate lo continuaron tres años después, en el siguiente Congreso Solvay.

Algunas de las objeciones propuestas por Einstein ayudaron a aclarar algunos conceptos de la nueva teoría. Sin embargo, una interpretación consistente del formalismo de la nueva mecánica cuántica hace inevitable la conclusión del indeterminismo. Aun Einstein, derrotado pero no convencido, tuvo que admitir que desde el punto de vista lógico la teoría y su interpretación forman un sistema consistente de pensamiento.

A partir de 1927 la interpretación de Copenhague de la mecánica cuántica fue la aceptada por la mayoría de los físicos. Einstein nunca dudó que la nueva mecánica cuántica diera resultados correctos, sin embargo, siempre creyó que su formulación no era completa. Tuvo la esperanza de que se desarrollara una teoría completa, que englobara a la mecánica cuántica, en la cual la causalidad y el determinismo fueran su parte fundamental. Es de justicia decir que se han hecho variados intentos a lo largo de esta líneas, sin embargo, hasta hoy no se ha logrado construir una teoría completamente consistente.

La mecánica cuántica formulada por Heisenberg, Schrödinger, Born y otros es la que actualmente se utiliza para la solución de un gran número de problemas físicos, químicos y hasta biológicos.

Vemos así que Albert Einstein fue el que desde el inicio desarrolló las ideas cuánticas. En particular, él creyó y demostró que la cuantización era algo real; fue el motor del avance de la mecánica cuántica. Sin embargo, al exponerse en forma coherente la nueva teoría no estuvo de acuerdo con las conclusiones básicas acerca de la indeterminación. Alguna vez hizo el comentario que ilustra su posición: "Yo creo que Dios no juega a los dados."

Para finalizar, quisiéramos destacar un hecho que es importante: la actitud que tomó Einstein al atacar algún problema físico. Trabajó en temas muy concretos que no habían tenido solución satisfactoria, como el efecto fotoeléctrico o el de los calores específicos, pero no tanto para resolver específicamente esas cuestiones pendientes, sino como herramienta que le ayudó a esclarecer ideas y principios fundamentales, mucho más generales que los del problema específico que estaba tratando. Así, cuando trabajó en el efecto fotoeléctrico no fue tanto para sacar del impasse una situación que no tenía entonces explicación, sino que resolvió este problema como parte de una idea más general, el carácter corpuscular de la luz. Asimismo, resolvió el problema del calor específico a bajas temperaturas, haciendo ver que esto era una manifestación de un fenómeno mucho más general. Esta forma de proceder fue una característica muy singular de Einstein. Se puede decir que su interés primordial fueron los principios básicos y no tanto los detalles del efecto fotoeléctrico o del calor específico.

El papel fundamental de Albert Einstein en la concepción y desarrollo de la mecánica cuántica no es muy conocido entre el gran público. Una razón de ello es el enorme prestigio que tuvo por haber desarrollado la teoría de la relatividad tanto especial como general. Esta fama simplemente enmascaró sus otras actividades que fueron esenciales en la construcción de la física moderna.

 

Figura 1. Einstein y su primera esposa, Mileva Maric, en 1911, poco después de cumplir ambos los 30 años (en Zurich).

Figura 2. Einstein con Ehrenfest y su hijo en Leyden. Junio de 1920.

Figura 3. Einstein a los 50 años con Elsa su segunda esposa, y su hijastra Margot, en su casa de Berlín.

Figura 4. Einstein con Irene Joliot-Curie, hija de madame Curie.

Figura 5. Einstein en su estudio de la Universidad de Princeton, EUA.

Figura 6. Un hermoso estudio fotográfico de Einstein.

Figura 7. Einstein tocando el violín. Fotografía sin fecha, supuestamente tomada a bordo del barco que lo llevó a los Estados Unidos en 1930.

Figura 8. Einstein en la torre del telescopio solar del observatorio de Mount Wilson, California, en 1930. Al extremo derecho está el doctor St. John, director del observatorio. Se cree que la persona del centro, probablemente su intérprete, era su ayudante, el doctor Meyer.

NOTAS

1 Un átomo está ionizado si, de alguna forma, se le han unido algunos de sus electrones. El helio ionizado es un átomo que tiene un núcleo con dos cargas positivas y un solo electrón a su alrededor.

2 La palabra "láser" es un acrónimo en inglés de amplificación de luz por emisión estimulada de radiación.

3 G.P. Thomson fue hijo único de J. J. Thomson (más conocido como J. J.) quien descubrió en 1897 la partícula que llamó electrón y luego recibió el premio Nobel de Física en 1906.