III. INTERFERENCIA

EN ALGUNA ocasión hemos visto pompas de jabón. Si las observamos con detenimiento nos damos cuenta de que muestran diversos colores.

Otra experiencia que seguramente el lector ha tenido es la de ver en la calle, después de que ha llovido, el agua que cayó sobre aceite. Uno observa que el charco de agua tiene diversos colores.

Estos fenómenos son dos ejemplos de interferencia de luz, fenómeno que ocurre cuando dos haces de luz llegan a la misma región del espacio. Veamos con detenimiento este fenómeno.

Supóngase que dos ondas como las mostradas en las figuras 8(a) y 8(b) llegan a una región del espacio. El efecto neto que producen estas ondas en cada punto es la combinación de ambas. Esta última afirmación significa lo siguiente: consideremos el punto P, en el cual la onda a tiene una amplitud representada por AB, mientras que la onda b tiene una amplitud dada por CD; notamos que ambas amplitudes tienen el mismo sentido, es decir, hacia arriba; por tanto, la amplitud neta en el punto P es la suma de las amplitudes AB más CD, que da la amplitud AD mostrada en la figura 8(c). Siguiendo este procedimiento para cada punto, encontramos que la onda resultante de la combinación de las ondas a y b es la onda c mostrada en la figura 8. Se dice que la interferencia de las ondas a y b da lugar a la onda c.

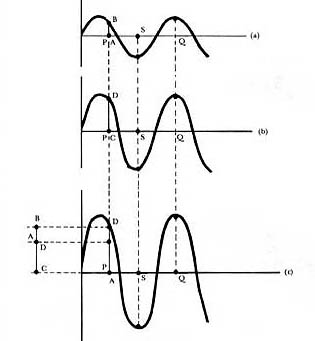
Figura 8. Dos ondas en fase, (a) y (b), interfieren constructivamente dando como resultado la onda (c).

En el caso particular que estamos tratando, nos damos cuenta de que las ondas que interfieren son tales que cuando una de ellas tiene un máximo, la otra también lo tiene (punto Q de la figura 8); mientras que cuando una de ellas adquiere un mínimo, la otra también lo adquiere (punto S de la figura 8). Se dice que las ondas que interfieren están en fase. Vemos que la onda resultante (c) tiene una amplitud igual a la suma de las amplitudes de cada una de las ondas que interfieren. Las ondas, por decirlo así, se refuerzan una a la otra. Este caso se llama interferencia constructiva.

Puede darse también otra situación en que las ondas que interfieren sean tales que cuando en un punto determinado una de ellas tenga una amplitud en un sentido, la otra tenga una amplitud en el otro sentido, como se muestra en la figura 9. Se dice que estas ondas están fuera de fase. Consideremos el punto P, en el cual la onda a tiene amplitud AB y la onda b tiene amplitud CD. A diferencia del caso arriba tratado, ahora los sentidos de las ondas son opuestos; mientras una tiene amplitud hacia arriba, la otra tiene amplitud hacia abajo. Por lo tanto, la amplitud neta ahora es la diferencia entre AB y CD, que da el valor RL mostrado en la figura 9 (c). La onda resultante es la c. Notamos que en este caso la amplitud de la onda resultante es menor que la que tiene la onda de la figura 8(b). Por decirlo así, una onda cancela el efecto de la otra. Hay interferencia destructiva. Si ocurriese el caso en que las ondas que interfieren tuvieran justamente la misma amplitud, pero estuvieran absolutamente fuera de fase, entonces la cancelación sería completa; en este caso las cantidades AB y CD serían iguales, por lo que su diferencia RL sería cero. En consecuencia, el resultado neto es que ñno hay onda! La interferencia es ahora completamente destructiva.

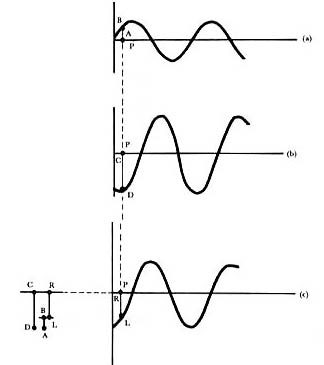
Figura 9. Dos ondas fuera de fase, (a) (b), interfieren destructivamente dando como resultado la onda (c).

Si las ondas que interfieren son tales que no están en fase ni completamente fuera de fase, la interferencia da lugar a una onda como la mostrada en la figura 9(c). No hay ni reforzamiento ni destrucción completos, se da una combinación intermedia entre los casos arriba descritos.

Los efectos de la interferencia tanto constructiva como destructiva se pueden observar con la luz en un experimento como el que se describe a continuación:

Consideremos una fuente de luz S (Figura 10) de un solo color. Esto significa que se tiene una onda de una sola longitud de onda bien determinada. Se hace incidir la luz que sale de la fuente sobre una pantalla FG que tiene dos rendijas A y B. Si no hubiese difracción de los haces de luz en cada una de las rendijas, entonces en la pantalla LK solamente quedarían iluminadas las zonas RS y TU. Sin embargo, si la longitud de onda de la luz incidente es del mismo orden que las dimensiones de las rendijas, entonces cada una de ellas difracta al haz que pasa por ellas y en un punto como el Q, que no está dentro de los haces BUT o ASR, llegan dos ondas, provenientes de cada una de las rendijas, y estas dos ondas interfieren. Así del otro lado de la pantalla FG existen dos ondas que interfieren.

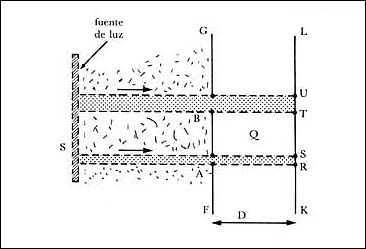
Figura 10. Si la luz se propagara en línea recta solamente quedarían iluminadas las zonas UT y SR.

Consideremos ahora lo que ocurre en la pantalla KL. En un punto de la pantalla como el O (Figura 11) las dos ondas llegan en fase, por lo que hay interferencia constructiva. En consecuencia, en el punto O debe verse luz intensa. En un punto como el P, las ondas llegan completamente fuera de fase, por lo que hay interferencia destructiva. Por lo tanto, en P no hay luz, es decir, debe estar oscuro. En otro punto como el Q, las ondas llegan en fase, por lo que debe haber luz intensa, etc. Esto significa que en la pantalla KL debemos ver bandas de luz intensa seguidas de bandas oscuras. Efectivamente esto es lo que ocurre. En la figura 12 se muestra lo que se observa en la pantalla KL. En este patrón de interferencia se aprecian bandas de luz intensa seguidas de bandas completamente oscuras.

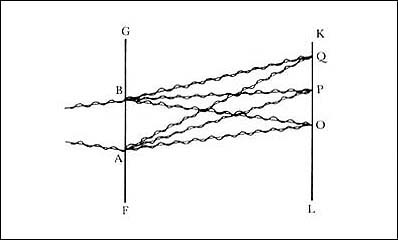
Figura 11. Al pasar las ondas por cada rendija se doblan, debido a la difracción, e interfieren. En el punto O las ondas llegan en fase; en el punto P llegan fuera de fase; en el punto Q llegan en fase, etcétera.

Figura 12. Patrón que se forma en la pantalla KL de la figura 11.

Regresando a los fenómenos mencionados al principio de este capítulo, solamente queremos mencionar que tanto en la pompa de jabón como en el charco con aceite la luz blanca que llega, por ejemplo, la del Sol, se separa en varios rayos y los así formados interfieren dando lugar a patrones de interferencia. Ahora bien, dado que el patrón de interferencia que se forme depende de la longitud de onda de la luz y en vista de que la luz blanca está compuesta de muchos colores, es decir, de muchas longitudes de onda, entonces cada color forma un patrón característico. Las posiciones de los máximos iluminados dependen de la longitud de onda; diferentes longitudes de onda resultan en diferentes posiciones de sus máximos. Lo que vemos entonces es la combinación de los patrones de interferencia para diferentes colores. Ya que el patrón de interferencia que se forme depende de la longitud de onda de la luz, al ocurrir este fenómeno la luz blanca se separa en sus componentes. Es por ello que en la pompa y el charco observamos diversos colores.

Volvamos al caso de la figura 12. Las posiciones en que se encuentran tanto los puntos iluminados como los oscuros dependen de varias cantidades: de la distancia AB entre las rendijas, de la distancia D entre las pantallas FG y KL y de la longitud de onda de la luz que se usa. En efecto, si se cambia la posición de la pantalla LK entonces los puntos en que las ondas están en fase ya no serán los mismos que cuando la distancia era D; lo mismo pasa para aquellos puntos en que las ondas están fuera de fase. De manera similar, cuando se cambia la distancia AB entre las rendijas, la separación entre las ondas que interfieren cambia y por consiguiente, los puntos de interferencia tanto constructiva como destructiva cambian. Asimismo, al variar la longitud de onda de la luz incidente, también cambia visiblemente el patrón de interferencia que se forma.

La relación entre los factores de los que depende el patrón de interferencia puede usarse de diferentes maneras, como se describe a continuación.

Una posibilidad es dar el valor de la longitud de onda de luz incidente así como las características geométricas tanto de la rendija como la distancia entre las pantallas. Entonces es posible predecir el patrón de interferencia que se formará en la pantalla LK.

Otra posibilidad es dar las características geométricas del arreglo, es decir, la distancia entre las rendijas y la distancia D entre las pantallas y además dar el patrón de interferencia que se forma en LK. Dado este patrón, uno puede medir la distancia que hay entre el centro de una banda iluminada y el centro de una banda oscura. Con todos estos valores se puede inferir el valor de la longitud de onda de la luz incidente. Usado de esta manera, este arreglo se llama espectroscopio de interferencia. Este aparato sirve para encontrar los valores de las longitudes de onda de haces luminosos.

Finalmente, si se da el patrón de interferencia que se forma en la pantalla LK así como la longitud de onda de la luz incidente, se pueden inferir las características geométricas de arreglo. Es decir, es posible obtener entonces, por ejemplo, el valor de la longitud de la separación entre las rendijas. Es esta última aplicación la que nos interesará más adelante.