V. CRISTALES

DESDE tiempos lejanos el hombre ha conocido el cuarzo, que es una sustancia mineral y cuya composición química es bióxido de silicio (SiO₂). Este compuesto es uno de los minerales más comunes y se presenta en la naturaleza en variadas formas, una de las cuales es transparente. Por este motivo los griegos le llamaron crystallos, que quiere decir "hielo claro", pues creían que se formaba de agua en el frío intenso de los Alpes; de allí el nombre de cristal, o más comúnmente, cristal de roca, usado para dicha variedad. Además del cristal de roca, existen otras variedades del cuarzo que tienen distintos colores, entre las que podemos mencionar como ejemplos la amatista, el ojo de tigre, etcétera.

Los cristales de cuarzo tienen la característica de que sus superficies forman figuras geométricas bien determinadas. Ocurren en formas prismáticas con caras lisas. Así, una variedad común del cuarzo se presenta en forma de doble pirámide (Figura 16(a)); otra variedad adquiere la forma de una bipirámide hexagonal con un prisma (Figura 16(b)), mientras que en otras ocasiones presenta una forma distorsionada (Figura 16(c)).

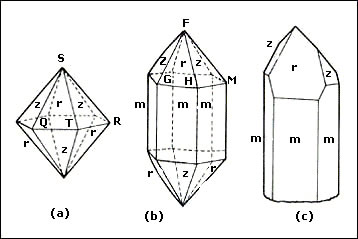
Figura 16. Formas que tienen diversas variedades de cristales de cuarzo.

La belleza y elegancia de los cristales han sido motivo constante de admiración. En 1611 Johannes Kepler conjeturó que los cristales deberían tener una estructura interna periódica. Posteriormente, en 1664 el científico inglés Robert Hooke escribió sobre la regularidad de la forma de diferentes cristales y especuló sobre el porqué de ello. Formuló la hipótesis de que esto era el resultado de un empaquetamiento ordenado de partículas esféricas dentro del cristal.

En 1669 el médico danés Nicolaus Steno descubrió que aunque las caras del cuarzo presentaban variaciones en su forma y en su tamaño, dependiendo de las condiciones en las cuales el cristal se formó, los ángulos entre las caras correspondientes eran siempre iguales. Es decir, por ejemplo, el ángulo que forman las caras QST y TSR en el cuerpo de la figura 16(a) es igual al ángulo que forman las caras GFH y HFM del cuerpo de la figura 16(b).

Además del cuarzo, en el siglo XVII se conocía un gran número de otras sustancias que también presentan caras en su superficie y para las cuales parecía también ser cierta la observación de Steno de que los ángulos entre sus caras son iguales, a pesar de que se presentan en diversas variedades.

Los pensadores de la época se convencieron de que esta constancia de los ángulos entre las caras de una forma cristalina de una sustancia determinada debe ser reflejo de cierta regularidad en su estructura interna.

Años después, en 1772, el francés Romé de Lisle, después de un estudio muy sistemático, descubrió que estos ángulos entre las caras de un cristal son característicos de la sustancia, o sea, un mineral presenta siempre el mismo ángulo entre sus caras sin importar el lugar de donde se le haya extraído o las condiciones en que haya cristalizado la sustancia. Por otro lado, distintos cristales tienen distintos valores de los ángulos entre los planos que forman sus caras. Cada sustancia, por lo tanto, tiene un valor bien determinado de dicho ángulo. El valor del mencionado ángulo ha servido para saber qué cristal se tiene, es algo así como la "huella digital" del cristal.

Otra propiedad de los cristales que ya se conocía era la facilidad con que se parten. Resulta que los cristales tienden a romperse con relativa facilidad a lo largo de ciertas superficies, mientras que prácticamente no se rompen en otras direcciones. Estas superficies son justamente las mismas de las que se habló en los párrafos anteriores. Más adelante volveremos a hablar al respecto.

En 1774 el fránces René Just Hañy publicó un libro Essai d'une théorie sur la structure des cristauxen el cual hizo ver que la propiedad que tienen los cristales de formar ángulos bien determinados entre sus caras se podría explicar si se supone que internamente están formados por unidades que se repiten (Figura 17), en forma análoga a aquélla en que se repiten los ladrillos de un muro. La única diferencia consistiría en que la unidad o "ladrillo" que se repite en el cristal lo hace en todo el espacio, o sea en tres dimensiones, y no solamente a lo largo de una superficie plana como ocurre con el muro. Además, con esta hipótesis Hañy pudo explicar otras propiedades de los cristales, como la extraordinaria simetría y regularidad que muestran y la de romperse a lo largo de ciertas superficies.

Figura 17. Formación de cristales a partir de la repetición de una unidadd elemental, según Hañy.

Con el desarrollo de las ideas sobre la estructura atómica de la materia, se pensó que era claro que la simetría macroscópica de los cristales era un reflejo de que los átomos o moléculas que formaban la sustancia estaban dispuestos en forma ordenada. Hacia mediados del siglo XIX el francés A. Bravais formuló la hipótesis de que las moléculas de un cristal formaban un patrón estructural que al repetirse traslacionalmente en tres dimensiones formaba el cristal. Este patrón estructural, llamado la celda unitaria, estaría formado por un átomo o una molécula o un complejo de moléculas y sería el "ladrillo" básico con el que se construiría el cristal. La analogía en dos dimensiones sería el patrón que tiene el papel tapiz con el que se suele cubrir las paredes de las habitaciones. Se puede uno dar cuenta que este patrón se repite al trasladarlo a lo largo del papel. De esta manera, con la hipótesis de la celda unitaria Bravais pudo explicar algunas características de los cristales así como las diferencias que para entonces ya se habían encontrado entre diversos cristales.

Sin embargo, hasta principios del siglo XX no hubo manera de demostrar directamente la hipótesis formulada por Bravais. En particular no se podía determinar cómo estaba construida la celda unitaria. Hasta esa época no se conocía prácticamente nada acerca de la estructura de los átomos en los sólidos. No se había progresado más allá de medir y registrar las características de las caras externas de los cristales, logrando solamente identificar y clasificar minerales. Se trataron de aplicar métodos químicos que no fueron útiles para resolver esta cuestión, pues para su uso los sólidos se tenían que calentar, evaporar o mezclar en soluciones, y al realizar estas operaciones, el sólido perdía justamente las características microscópicas que se querían determinar. Se requería de un tipo de análisis que no destruyera la muestra que se estuviese analizando.

En 1912 la situación cambió radicalmente cuando Max von Laue descubrió que la difracción de rayos X podría proporcionar la clave para la determinación de la estructura interna de los cristales. Pero antes de continuar, hablaremos en el siguiente capítulo sobre los rayos X.