II. LOS AÑOS EN BERNA
| Realmente fueron hermosos aquellos años en Berna. A. EINSTEIN |
EINSTEIN permaneció en Berna hasta finales de 1909: cuando salió
de ahí para tomar su puesto de profesor asociado en la Universidad de Zurich,
había ya escrito el trabajo en que propone que la luz tiene naturaleza cuántica
y que le valiera el premio Nobel; participado decisivamente en la demostración
definitiva de la estructura atómica de la materia y creado la mecánica estadística
y la teoría del movimiento browniano; inventado la teoría especial de la relatividad
e iniciado la construcción de la teoría general de la relatividad; además, había
descubierto la que probablemente es la más famosa fórmula de la física contemporánea:
E= mc² como el corrimiento de la luz hacia el rojo y fundando
la teoría cuántica de los sólidos. Lleva entre sus papeles su primer doctorado
honoris causa y antes de un año sería propuesto por primera vez para
el premio Nobel. Cómo sucedió todo esto trataremos de contarlo en este capítulo.
Berna es una pequeña ciudad de carácter universitario, casi milenaria y hermosa. Einstein tuvo la fortuna de instalarse en el número 49 de la Kramgasse, de la que Goethe en sus Viajes a Suiza dijera que es la más bella calle de esta pulcra ciudad. El pequeño departamento en el último piso que ocuparan los Einstein es hoy museo y está abierto al público. En este departamentito vivió Einstein durante 1905, el annus mirabilis, no sólo de Einstein, sino de la física, el curso del cual le fue suficiente para ensanchar los horizontes de la física, como nunca nadie, antes o después de él pudo hacerlo en tan corto tiempo y a tal profundidad, con la única excepción de Newton.
Einstein permaneció en la Oficina de Patentes hasta finales de 1909, habiendo obtenido promoción a experto técnico de segunda clase en 1906. En febrero de 1908 probó suerte como profesor privado (es decir, pagado por sus alumnos) en la Universidad de Berna, mermando con ello su limitado tiempo libre para investigar. Finalmente logró el puesto antes mencionado en la Universidad de Zurich, en la que no permanecería por mucho tiempo. Es sumamente interesante conocer cómo obtuvo Einstein su primer puesto de profesor.
En 1908 la Universidad de Zurich decidió crear la cátedra de física teórica; entre los posibles candidatos a ocupar el correspondiente puesto de profesor asociado se encontraban Einstein y su excompañero de estudios en la ETH Friedrich Adler (1879-1960), hijo de Viktor Adler, uno de los fundadores del Partido Socialdemócrata austriaco. Por simpatías políticas —y sin demérito de Adler— el puesto se le ofreció a este último. Cuando el joven Adler se enteró que Einstein sí tendría interés en el puesto en un acto pleno de integridad y lealtad escribió una carta al Comité de Educación, en la que decía que: "Si es posible obtener una persona como Einstein para nuestra Universidad, es absurdo darme a mí el puesto. Debo decir francamente que mis habilidades como investigador en física no soportan la menor comparación con las de Einstein. Una oportunidad como la presente de conseguir una persona que nos puede beneficiar tanto, elevando el nivel general de la Universidad no debe perderse debido a simpatías políticas." Adler tuvo aún que insistir durante varios meses para lograr que Einstein fuera el seleccionado. La amistad duró toda la vida, pero no estuvo libre de dificultades. En 1916, en plena Guerra Mundial e impulsado por su profundo pacifismo, Adler mató en un atentado al Primer Ministro austriaco; Einstein se ofreció como testigo de descargo. Ésta fue una de las primeras intervenciones pacifistas públicas de Einstein, de las cuales habría muchas en su vida.
Retomemos el hilo inicial. Einstein se ha establecido en Berna, tiene una situación personal modesta pero estable; ha publicado un par de trabajos científicos y le bulle la cabeza con ideas e interrogantes sin respuesta. Y llega 1905, año en que sucede todo como un milagro: en marzo escribe el trabajo de la cuantización de la luz y el efecto fotoeléctrico; en abril su tesis doctoral —que hoy en día, 80 años después, sigue siendo uno de sus trabajos más citados por su interés industrial— en mayo escribe su primer ensayo sobre la teoría del movimiento browniano; y, aunque parezca increíble, un mes después, en junio, envía a publicación el trabajo que da nacimiento a la teoría de la relatividad. Y en septiembre de este mismo año, Einstein expide el manuscrito que contiene la fórmula que relaciona la masa con la energía. En el ínterin, usa las vacaciones de verano para ir a Yugoslavia y conocer a la familia de su esposa. Revisaremos los trabajos de 1905 en su orden cronológico, para asomarnos a las teorías que propusiera Einstein en sus años en Berna.
El trabajo sobre la radiación electromagnética, en el que Einstein propone que la luz está constituida por corpúsculos, más conocido como el trabajo sobre el efecto fotoeléctrico, tiene su origen en un viejo problema de la física teórica, al que el gran físico alemán Max Planck (1858-1947) había encontrado solución parcial en 1900, el año de la graduación de Einstein.
El problema en cuestión es el llamado de la radiación de un cuerpo negro, es decir, de un cuerpo que absorbe toda la luz que cae sobre él. Cuando un cuerpo negro es calentado emite radiación electromagnética. Algo similar a lo que sucede cuando calentamos un horno y sentimos cómo la radiación emitida nos quema. Más aún, si lo calentamos a temperaturas muy altas, podemos ver la radiación emitida, parte de la cual cae en la región visible del espectro. El problema se presentó cuando los físicos se preguntaron cuánta luz emite un cuerpo negro en las altas frecuencias (cuánta en la azul, cuánta en la violeta, y cuánta más allá, en el ultravioleta, rayos x, etc., hasta el infinito) y cuánta en las bajas frecuencias. El problema tiene importancia teórica —por razones que no viene al caso detallar— y grande fue el desconcierto cuando se encontró que la física clásica (en este caso, la teoría de Maxwell combinada con la teoría del calor o termodinámica) predice que debe haber mayor radiación conforme más alta es la frecuencia —debido a que hay muchas más frecuencias altas que bajas y todas tienen iguales posibilidades de aparecer—. Pero este resultado está equivocado, pues si fuera cierto significaría que prácticamente toda la radiación sería a frecuencias muy, muy altas, y se observa que éste no es el caso. Por ejemplo, conforme calentamos el horno, vemos que el color de la luz radiada va cambiando; pasa de rojizo, a rojo subido, a naranja, a azuloso finalmente, pero no es violeta ni menos aun ultravioleta a cualquier temperatura.
Los físicos del siglo pasado lograron encontrar dos fórmulas para describir parcialmente este fenómeno; una es la fórmula de Rayleigh, derivada con los métodos de la física, que describe correctamente lo que se observa a bajas frecuencias pero no a las altas. La otra es la fórmula de Wien, que no tenía justificación teórica alguna pero ajustaba excelentemente los datos experimentales a altas frecuencias, pero no a las bajas. Planck se dio a la tarea de entender este problema y en 1900 pudo ofrecer una fórmula —famosísima, y que lleva su nombre— que describe correctamente los datos observacionales a todas las frecuencias y a todas las temperaturas. El punto crucial está en que para obtener su fórmula, Planck tuvo que introducir una hipótesis por demás extraña: la energía electromagnética que absorbe o que emite un cuerpo negro viene en "paquetes" y sólo se pueden intercambiar paquetes enteros de energía. Como en los supermercados: se puede comprar uno, dos..., cien kilos de azúcar, pero no kilo y cuarto, por ejemplo. A estos paquetes de energía electromagnética Planck los llamó cuantos (o quantos; palabra latina que significa precisamente cuanto). Se considera a este trabajo como la primera piedra de la física moderna y a Planck, en consecuencia, como el fundador de las teorías cuánticas. Sin embargo, un largo camino tenían aún los físicos por delante.
El problema se quedó aquí, donde Planck lo dejó, por varios años. Aunque estaba claro que la fórmula de Planck era correcta, la idea de introducir un elemento tan exótico como el cuanto de energía no convencía a nadie —de hecho, ni al propio Planck, quien durante varios años hizo un tan inútil como honesto esfuerzo por rederivar su fórmula sin romper tan bruscamente con los principios clásicos—. Como veremos más adelante, a finales del siglo pasado todavía no era universalmente aceptada la idea de que la materia tiene estructura molecular —grandes figuras como Ostwald y Mach consideraban a las moléculas como meras ficciones—. La razón atrás de esta actitud se puede encontrar en la convicción de que la naturaleza es continua, pues todas las ecuaciones de la física teórica de la época eran perfectamente consistentes con esta hipótesis. Luego para la física clásica la noción de una estructura discreta, granular, es superflua. Y es principio general de la ciencia desechar lo superfluo. 1 Pero si los físicos de 1900 no estaban aún en condiciones de aceptar como establecida la naturaleza granular de la materia, ¿menos aún estaban dispuestos a oír hablar de granos de energía luminosa! 2
En 1905 Einstein retomó este problema, pero desde un ángulo enteramente nuevo. Como veremos más adelante en este mismo capítulo, para esas fechas Einstein había ya elaborado una teoría que le permitía calcular el comportamiento estadístico de sistemas constituidos por muchos cuerpos, como los gases compuestos por moléculas y cosas similares. Los detalles los dejamos para más adelante, aceptando por el momento que Einstein disponía de herramientas teóricas, que él mismo había creado, para hacer estudios estadísticos. Bien, pues a Einstein se le ocurrió hacerse una pregunta: ¿Qué pasa si aplico mis métodos estadísticos al problema del cuerpo negro? De hecho Einstein tenía dos posibilidades: una era aplicar sus métodos estadísticos y usar la fórmula de Rayleigh, es decir, estudiar un problema puramente clásico (y el resultado seguramente estaría mal); la otra era hacer lo mismo, pero con la fórmula de Planck (y el resultado sería seguramente novedoso, pero correcto). Einstein calculó entonces lo que se llaman las fluctuaciones de la energía de la luz. 3 El cálculo le mostró que la fórmula de Planck predecía lo mismo que la de Rayleigh, pero agregando un término adicional a las fluctuaciones: la energía de un cuerpo negro fluctúa más que lo que dice la física clásica. Pero Einstein dio otro paso adelante. Comparó sus resultados con los que había obtenido pocos años antes para las fluctuaciones de la energía de un gas diluido y encontró algo sorprendente: ¡eran iguales a las del nuevo término recién descubierto por él! ¡Luego aquí estaba la explicación a la hipótesis de Planck! Todo queda claro si aceptamos que en el campo electromagnético existen componentes similares a las moléculas de un gas, es decir, pequeños corpúsculos o "paquetes" luminosos que porta cada uno una energía definida y se pueden ver como "moléculas" de luz. Estas "moléculas" producen el término similar al de los gases, y el que se trate de luz, es decir, de ondas, explica el término que da la teoría de Maxwell. Con el curso de los años a estas "moléculas" electromagnéticas se les llamó fotones.
Einstein puso a prueba su hipótesis. Si la luz tiene una estructura granular, esto debe observarse no sólo en algún caso aislado como el estudiado por Planck, sino en multitud de situaciones diferentes. Pronto encontró un problema no resuelto e inintelegible para la física de su época, al menos tanto como el problema del cuerpo negro, y que se resolvía mágicamente con su hipótesis: el efecto fotoeléctrico consiste en que ciertos materiales, al ser expuestos a la luz, emiten electrones: el fenómeno fue observado y reportado por Hertz durante sus experimentos para producir ondas electromagnéticas. Cuando se le sometió a estudio experimental, se observó que tenía propiedades sorprendentes e inaccesibles para la física de la época, por lo que permaneció inexplicado. Entre estas propiedades ininteligibles mencionaremos las siguientes. Se observó que aumentando la iluminación —lo que significa dar mayor energía al material— no aumentaba la energía de los electrones emitidos, sino sólo su número; asimismo, se encontró que luz de diferentes colores podía producir efecto fotoeléctrico, pero que para cada material había un color —o mejor, una frecuencia— de la luz abajo de la cual simplemente desaparecía el fenómeno. Experimentalmente quedó claro que esta frecuencia de corte es característica de cada material.
Si pensamos en el efecto fotoeléctrico en términos de una onda electromagnética que incide sobre un átomo, el que absorbe su energía y libera un electrón, simplemente no podremos explicarnos este comportamiento, al menos si nos negamos a construir una teoría ad hoc que, por su carácter hechizo poco o nada explicaría y menos convencería. Pero Einstein vio el problema desde su nueva perspectiva, y notó que todo cambia de golpe desde ella. Pensamos en la luz como constituida por paquetes de energía de valor hf; un átomo absorbe un paquete y se queda con esta energía; parte de ella —o toda, en el mejor de los casos— se transfiere en alguna forma por los mecanismos internos atómicos a uno de los electrones del átomo. El electrón se acelera debido a esta energía y se escapa del átomo; pero como tiene que vencer la atracción del átomo ionizado que abandona, pierde una parte de esta energía, la que llamaremos W; luego la máxima energía con que el electrón puede escaparse es
| Emax = hf - W |
(1)
|
Ésta es la famosísima fórmula del efecto fotoeléctrico de Einstein. Veamos algunas de sus predicciones. Supóngase que hacemos una serie de experimentos fotoeléctricos cambiando en cada ocasión la intensidad de la luz, pero sin cambiar el color. Como f es fija, nada cambia en la fórmula (1) en cada experimento, por lo que observamos cada vez la misma Emax, sólo que cuando la luz sea más intensa habrá más paquetes de energía hf disponibles y veremos más electrones liberados. Repitamos ahora los experimentos, pero manteniendo fija la intensidad y variando el color de la luz; cuando lleguemos a una frecuencia de luz tan baja que hf adquiere el valor W o un valor menor, la energía E de que pueden disponer los electrones se reduce a cero y no puede haber más efecto fotoeléctrico. Luego existe una frecuencia de corte del fenómeno que está dada por la fórmula
|
(2)
|
Las propiedades que acabamos de deducir son precisamente las observadas para el efecto fotoeléctrico; luego la teoría es cualitativamente correcta. Para comprobar la validez de las predicciones cuantitativas de la teoría, todo lo que tiene que hacerse es probar la fórmula (2). Ésta es una fórmula muy interesante, que dice que la energía W y la frecuencia de corte de un fotocátodo dado deben tener un cociente cuyo valor no depende del material que se use para construir el dispositivo y que esta constante es precisamente la de Planck. Luego aquí hay un método novedoso para hacer una determinación no termodinámica de la constante de Planck.
La teoría de los cuantos de luz propuesta por Einstein encontró mucha resistencia. En particular, el notable físico experimental norteamericano Robert Millikan (1868-1953) no creyó en ella y se propuso mostrar su invalidez probando experimentalmente que la fórmula (2) conducía a resultados erróneos. Después de un meticuloso y largo trabajo, concluyó que el valor de la constante de Planck determinado con los métodos fotoeléctricos coincide con el valor previamente establecido con ayuda del cuerpo negro y reconoció la validez de la teoría. En la actualidad, el método fotoeléctrico es usado en los laboratorios de enseñanza para medir el valor de h. Aun así, tuvo que pasar mucho tiempo para que la teoría de los fotones de Einstein alcanzara aceptación general, lo que sucedió alrededor de 1923, gracias en mucho a los trabajos experimentales del físico norteamericano Arthur Compton (1892-1962).
Pese al escepticismo general con que fue recibida la hipótesis de la cuantización de la luz, Einstein la desarrolló tanto como le fue posible y trabajó sobre el tema desde muy diversos ángulos por casi dos décadas. Pero Einstein pronto comprendió que era posible y necesario generalizar su hipótesis de cuantización. En particular entendió que no hay razón alguna para pensar que sólo los osciladores del campo electromagnético tienen propiedades cuánticas: precisamente, la hipótesis opuesta, es decir, que todos los osciladores deben poseer propiedades cuánticas, parece más natural. Para poner a prueba esta nueva hipótesis, Einstein la aplicó en 1906 a los átomos que forman un cuerpo sólido calculando lo que en el lenguaje de los físicos se llama el calor específico de un sólido, que es una propiedad que depende del material del que está hecho y mide cuánto aumenta su temperatura cuando le suministramos una cantidad fija de calor al cuerpo.
Desde principios del siglo XIX se sabía por vía experimental que el calor específico de los sólidos simples es una constante, la misma para todos, cuando se mide en unidades apropiadas. En 1876 Boltzmann pudo explicar teóricamente este hecho, basado en un resultado muy general de la teoría cinética: el teorema de equipartición de la energía, el cual establece que una vez alcanzado el equilibrio, los osciladores tridimensionales que forman la malla de un sólido simple tienen cada uno la misma energía de oscilación, cualquiera que sea su frecuencia de oscilación. Esto determina que el calor específico del cuerpo sea constante.
Ahora bien, la situación real era un tanto más compleja que lo descrito, pues se sabía que aunque en la gran mayoría de los casos el calor específico observado correspondía al esperado, también se conocían desviaciones de esta simple ley. Por ejemplo, que el diamante tiene un calor específico varias veces menor que el valor usual. Y, para complicar las cosas, trabajos de Heinrich Weber, James Dewar y otros físicos habían mostrado que para algunas sustancias, entre ellas el diamante, el calor específico decrece al reducirse la temperatura del cuerpo. Sin embargo, la tendencia general era considerar estas excepciones como tales, intentando explicarlas con ideas particulares, corno que algunos de los osciladores del cuerpo se van "apelmazando" al bajar la temperatura. En otras palabras, aunque se estaba frente a observaciones no entendidas del todo, no se sentía la existencia de ningún problema de fondo en conexión con los calores específicos de los sólidos en la época en que Einstein abordó el tema.
Pero las cosas se presentan en otra forma desde la perspectiva de Einstein. Si consideramos a los átomos que constituyen la malla del sólido como pequeños osciladores cuánticos de frecuencia f, entonces cada uno tendrá una energía hf si la hipótesis cuántica es correcta. Esto quiere decir que no es cierto que cada oscilador tiene una energía independiente de su frecuencia, como afirmaría la ley clásica de equipartición. Calcula Einstein entonces el calor específico del sólido usando la fórmula de Planck (que es la que describe osciladores cuánticos) en vez de la de Rayleigh (que es la que describiría osciladores clásicos) y encuentra que el resultado depende de la temperatura, aunque a temperaturas suficientemente altas (la temperatura ambiente para la mayoría de los materiales) se recupera el resultado clásico. Unos cálculos numéricos sencillos muestran que la curva que da la nueva teoría se ajusta bastante bien a las desviaciones para el diamante y otros elementos. Luego, contrariamente a los que se creía, las desviaciones conocidas de los calores específicos de su valor clásico si apuntaban hacia un problema fundamental: en esos casos no se obedecen las leyes de la física clásica, sino de la física cuántica (la que tendría que construirse).
Este trabajo de Einstein es importante por dos razones al menos. Por un lado, permitió ver que el fenómeno de la cuantización —es decir, de la existencia de valores discretos, discontinuos, de la energía y otras cantidades físicas— no se circuscribe a un reducido grupo de casos más o menos singulares, sino que es una propiedad general de la naturaleza. De hecho, en el trabajo que preparó en 1909 como ponencia para un congreso en Salzburgo —que fue el primer congreso en que participó— fue aún más lejos, al señalar explícitamente, el primero entre todos, que la descripción cuántica tanto de la luz como de las moléculas deberá contener simultáneamente aspectos corpusculares y ondulatorios. Esto constituye el germen de lo que quince años más tarde sería la mecánica cuántica. En segundo lugar, es el primer trabajo en que se estudia un fenómeno cuántico en un sólido; puede decirse que con este trabajo Einstein fundó la física cuántica del estado sólido, que hoy constituye una de las ramas más estudiadas de la física, por sus enormes e importantes aplicaciones prácticas.
Nos regresamos a abril de 1905. Einstein acaba de escribir su trabajo sobre la cuantización de la luz y el efecto fotoeléctrico e inicia la escritura de su tesis doctoral. Tanto la tesis —publicada un año después— como el trabajo escrito a continuación, se refieren a un problema enteramente diferente: el movimiento browniano. ¿Qué es el movimiento browniano y por qué ocupa Einstein su atención en él? Para responder a estas preguntas debemos retroceder unos pocos años.
Como dijimos antes, a la entrada de nuestro siglo los físicos aún no habían adoptado unánimemente el modelo molecular de la materia. Pese a los enormes éxitos que los químicos habían alcanzado en la comprensión de varios problemas importantes a partir de la hipótesis de que la materia está constituida por moléculas —hipótesis enunciada en esta forma ya por el químico inglés John Dalton (1766-1844) en 1803—, y de que éstas a su vez están formadas por átomos; pese asimismo a que la propia física había avanzado considerablemente en la construcción de la teoría cinética de los gases, la profunda convicción reinante de que la naturaleza es esencialmente continua —y que podríamos en principio subdividir un trozo de materia en granos tan pequeños como queramos, sin límite alguno— conducía a muchos físicos, incluyendo grandes personalidades, a considerar al modelo molecular como algo útil, pero carente de mayor significado real.
Einstein —como muchos otros físicos de la tradición de Maxwell y Boltzmann— desde muy temprano aceptó el modelo molecular como una imagen relativamente fiel de la naturaleza y se impuso como tarea encontrar métodos capaces de poner en evidencia su validez en forma concluyente. Podemos considerar que el trabajo de investigación realizado por Einstein hasta 1905 es una etapa preparatoria para esta tarea —aunque también fue decisivo para sus estudios sobre la cuantización de la luz, como vimos en las secciones anteriores—. El problema que Einstein se planteó durante el periodo 1902-1904 fue el de derivar las leyes de la termodinámica como resultado del hecho de que la materia a escala macroscópica está constituida por un gran número de moléculas en agitación térmica. Debido al inmenso número de partículas involucradas, es imposible hacer una descripción detallada de lo que sucede, por ejemplo, en un gas; pero sí podemos pretender hacer una descripción estadística y crear con ello lo que se llama la mecánica estadística. En alguna forma, el embrión de esta idea se encuentra ya en los trabajos de Maxwell y Boltzmann sobre la teoría cinética de los gases. Una idea cercana a la de Einstein la había tenido pocos años antes el físico norteamericano Josiah Gibbs (1839-1903) para desarrollar la termodinámica química, pero sus trabajos eran prácticamente desconocidos en la Europa de principios de siglo; hoy se considera tanto a Gibbs como a Einstein los fundadores de la mecánica estadística. Fue precisamente el contar con los métodos de la mecánica estadística lo que le permitió a Einstein recorrer un camino tan complejo, diverso y novedoso en tan corto tiempo como lo hizo en 1905.
A Einstein se le ocurrió una idea innovadora para elaborar un método que permitiera "ver" directamente los efectos de la permanente agitación térmica de las moléculas de un cuerpo. Supongamos que un líquido contiene pequeñísimas partículas en suspensión, como podrían ser granos de colorante o de polen en agua, etc. Como debemos suponer que las moléculas del líquido se mueven al azar, estarán golpeando a la partícula en suspensión por todos lados y en todas direcciones permanentemente; el efecto de la gran mayoría de los impactos tenderá a cancelarse mutuamente pero será normal que quede un pequeño efecto residual que pondrá al grano en movimiento, ora para arriba, ora a la izquierda, y así sucesivamente. De este modo, debido al impacto de las moléculas, si el grano en suspensión es suficientemente pequeño, deberá tener un movimiento incesante altamente irregular y muy complicado: Einstein de inmediato percibió que aquí tenemos un mecanismo para ver el movimiento (errático) que constituye el calor y, mucho más importante, para ver un efecto directo del movimiento de las moléculas. Einstein no lo sabía, pero este fenómeno había sido observado —pero no explicado— varias décadas antes por el botánico escocés Robert Brown (1773-1858) —el mismo que observó que los tejidos vegetales es un elemento estructural regular y propuso el término núcleo para identificarlo— y por esta razón se le conoce como movimiento browniano.
Einstein fue capaz de elaborar una teoría estadística del movimiento browniano y de mostrar que a partir del seguimiento del movimiento de una de estas partículas bajo el microscopio era posible medir el tamaño de las moléculas del solvente. De hecho, durante el año de 1905 Einstein presentó varios métodos diferentes para determinar las dimensiones moleculares (en particular, éste es el tema de su tesis doctoral), y el mismo año de 1905 publicó diversas extensiones a su teoría original. Los resultados de Einstein 4 fueron rápidamente puestos a prueba en varios laboratorios, particularmente en el del físico francés Jean Perrin (1870-1942) y su grupo a partir de 1908, quienes pudieron determinar con los métodos de Einstein las dimensiones moleculares y el número de Avogadro (es decir, el número de moléculas que contiene un mol de un gas en condiciones normales de presión y temperatura). Los resultados finales fueron tan convincentes, que el mismo Oswald reconoció en las moléculas objetos reales y no meras ficciones de uso conveniente, dando por resuelto el asunto. Quien nunca pudo aceptar la realidad de las moléculas fue Mach.
A principios de mayo de 1905 Einstein envió su artículo sobre el movimiento browniano a los Annalen der Physik y pasó a ocuparse de otros asuntos. En junio envió a publicación el trabajo en que crea la teoría de la relatividad. Aparentemente, unas cuantas semanas le bastaron para construir está teoría; más, como hemos visto, atrás había una historia de búsqueda y meditación de casi una década. Einstein termina su artículo sobre la teoría de la relatividad agradeciendo a su amigo M. Besso la ayuda brindada para la construcción de la teoría a través de discusiones. En aquellos años, Besso trabajaba en la Oficina de Patentes junto con Einstein; de hecho, este último le había conseguido el puesto, en parte por ayudar al amigo, en parte para tenerlo cerca y poder discutir con él los problemas de principio que le inquietaban; Einstein escribió alguna vez que en Besso encontraba su mejor caja de resonancia en toda Europa. En una conferencia que dictó en Japón en 1922, Einstein recordó cómo, al día siguiente de una prolongada discusión con Besso, buscó al amigo simplemente para agradecerle la deliberación, comentándole que gracias a ella había logrado que todas las piezas del rompecabezas embonaran: cinco semanas después estaba listo el artículo más famoso de Einstein: "Sobre la electrodinámica de los cuerpos en movimiento", con el que nace la teoría de la relatividad.
Como vimos en el primer capítulo, Einstein veía muy claramente que las leyes de la vieja mecánica clásica y las de la teoría electromagnética de Maxwell —de creación reciente, pero muy bien fundada y comprobada— eran incompatibles; esto implicaba la necesidad de cambiar al menos una de estas teorías. Lo importante era entender qué es lo que debía cambiarse. Para Einstein había un dato cierto, que podemos inferir como sigue. En el experimento pensado del corredor alcanzando un rayo de luz, el corredor verá luz, cualquiera que sea la velocidad con que corra; pero la luz viaja a su velocidad c, pues de no ser así no sería la luz descrita por las ecuaciones de Maxwell. Luego debemos concluir que cualquiera que sea la velocidad del corredor, la luz que pasa a su lado viaja con la misma velocidad c. Esto quiere decir que la velocidad de la luz es la misma para todos los observadores, independientemente de la velocidad con que se muevan e independientemente de la velocidad de la fuente emisora. Después de verificar que esta conclusión es consistente con una serie de observaciones y fenómenos conocidos, Einstein la elevó a la categoría de principio: éste es uno de los dos principios en que se funda la nueva teoría. 5
Ahora podemos entender por qué fracasó el experimento de Michelson y Morley, y por qué dijimos que en su fracaso residía su importancia. En la concepción de este experimento se suponía que la velocidad de la Tierra se agregaría a la de la luz que llega frontalmente. Pero precisamente el postulado de Einstein dice lo contrario, es decir, que cualquiera que sea la dirección de la luz respecto al movimiento de la Tierra, mediremos la misma velocidad c. Luego si la hipótesis es cierta, el experimento debe fallar; y falló. Usualmente se considera a los experimentos de Michelson y Morley como un sólido soporte experimental para la teoría de la relatividad, aunque Einstein utilizó inicialmente otros efectos para llegar a esta conclusión.
Alcanzado este punto, el problema era construir una mecánica nueva que permitiera que la luz tenga la misma velocidad para todos los observadores, sea como sea que se muevan y sin introducir inconsistencias. Einstein encontró la salida llevando a sus últimas consecuencias una línea de pensamiento que había encontrado en Poincaré y Mach: las nociones de espacio y tiempo absolutos de la mecánica no son lógicamente necesarias ni están garantizadas por la experiencia. Un análisis profundo de este problema —estimulado por sus discusiones con Besso— le permitió a Einstein confirmar la idea —ya avanzada por Poincaré— de que el concepto de simultaneidad no tiene un carácter absoluto, sino que depende del estado de movimiento relativo. Esto quiere decir, por ejemplo, que si un observador parado en un andén considera dos eventos A y B como simultáneos, un viajero que los ve desde un tren en movimiento no los consideraría como simultáneos. Esto parece contradecir nuestra experiencia cotidiana, pero todo se resuelve cuando se observa que la diferencia de tiempo que el observador en el tren asignaría a los eventos es tan pequeña, que pasa totalmente desapercibida (¡precisamente por esto podemos usar la mecánica clásica!). Pero entonces, si es despreciable, ¿por qué hemos de preocuparnos por ello? El punto es de principio: ¿cuáles son las nociones correctas que debemos manejar al eliminar el espacio y el tiempo absolutos? Además, la diferencia es despreciable sólo debido a que el tren corre despacio; si su velocidad fuera muy alta, comparable con la de la luz, las diferencias podrían ser muy considerables. Basta que pensemos que si el portador de la lámpara corre a la velocidad de la luz, aun así la luz que pasa a su lado sigue viajando con la misma velocidad c, para que notemos qué diferente será esta nueva mecánica de la clásica.
Para estar en condiciones de construir la nueva mecánica, Einstein propuso un principio adicional: las leyes de la física deben ser las mismas para todos los observadores, independientemente de que unos se muevan uniformemente respecto a los otros. Éste, que no es sino una manera muy general de decir que no hay observadores privilegiados, "en reposo" respecto a algo (como podría ser un pretendido espacio absoluto o el éter), es el llamado principio de relatividad, del cual la teoría deriva su nombre. Este principio, en combinación con el de la constancia de la velocidad de la luz, le permitieron a Einstein construir la teoría especial de la relatividad. Puesto que el espacio y el movimiento absoluto desaparecen en esta teoría, Einstein propuso hacer a un lado por superflua la noción de éter. Nótese que en el principio de relatividad se toman en cuenta sólo observadores que se mueven uniformemente unos respecto a otros; debido a esta limitación se habla de teoría especial. Desde el principio Einstein mostró interés en extender la teoría a observadores en movimiento arbitrario y construir con ello una teoría general de la relatividad; la tarea resultó inmensa, y requirió de una década de esfuerzos, pero de ello hablaremos más adelante.
Vemos que la teoría de la relatividad es una nueva mecánica, consistente con la teoría de Maxwell y que rebasa a la vieja mecánica de Newton al eliminar sus elementos absolutistas. Estas dos mecánicas son prácticamente equivalentes (desde el punto de vista numérico) a las velocidades usuales, las que son muy pequeñas en relación con la velocidad de la luz, pero pueden diferir considerablemente para el caso de cuerpos que se mueven a grandes velocidades. Para estudiar el movimiento de un automóvil o un avión, incluso de un cohete interplanetario, seguimos usando la mecánica de Newton. Pero para una descripción correcta de los electrones o los protones en un acelerador de partículas, es indispensable hacer un tratamiento relativista.
Un primer resultado importante de la teoría de la relatividad es que ningún cuerpo puede alcanzar la velocidad de la luz: la velocidad c de la luz es un límite que la naturaleza impone al movimiento de cualquier cuerpo. Esto se debe a que la masa de un cuerpo resulta depender de su velocidad, siendo mayor conforme mayor es la velocidad, 1 y haciéndose infinitamente grande cuando el cuerpo alcanza la velocidad de la luz. Como ningún cuerpo puede tener una masa infinita (que sería mayor que la del Universo) tampoco puede alcanzar la velocidad c.
Otro resultado muy importante es que existe una equivalencia fundamental entre masa y energía. A esta conclusión llegó Einstein el mismo año de 1905, en su segunda nota sobre la teoría de la relatividad, enviada a publicación el mes de septiembre y se expresa mediante la famosa fórmula
| E = mc² |
(3)
|
En palabras, esta ley dice que un pedazo cualquiera de materia de masa m contiene una energía dada por el producto de la masa por el cuadrado de la velocidad de la luz; como la velocidad de la luz es una cantidad enormemente grande, la energía así calculada también resulta enorme.6 Quizá sea éste el resultado de la teoría de la relatividad que más consecuencias ha tenido para la humanidad. Es bien sabido que los reactores nucleares y las bombas atómicas trabajan convirtiendo parte de la masa de los núcleos atómicos en energía (que es liberada básicamente como energía térmica). La naturaleza usa en nuestro beneficio la misma solución, pues es una reacción nuclear que transforma masa en energía, la que mantiene ardiendo al Sol y a todas las estrellas y soporta la vida en la Tierra.
Otro resultado interesante de la teoría de la relatividad es que la longitud que le asignamos a una barra depende de si la medimos desde un sistema en reposo o en movimiento respecto de ella; 7 análogamente, el intervalo de tiempo que un observador asigna entre dos eventos, depende de la velocidad del observador. Un ejemplo de esta dilatación del tiempo es el siguiente. En la naturaleza existen muchas partículas que espontáneamente se transforman en otras y esto lo hacen en un tiempo fijo que les es característico. Por ejemplo, un pion decae espontáneamente en un muon y un neutrino 8 en aproximadamente un cienmillonésimo de segundo después de formado Sin embargo, si al generar el pion le damos suficiente energía para que se mueva a gran velocidad por ejemplo 0.99999 veces la velocidad de la luz, veremos que vive un tiempo 100 o más veces lo normal. Esto se debe a que el pion cuenta su tiempo desde su propio sistema y es respecto de él como vive su vida completa; pero ese cienmillonésimo de segundo visto desde el laboratorio, que se mueve respecto al pion a una velocidad muy cercana a la de la luz, se transforma por la dilatación relativista del tiempo en un intervalo centenares de veces mayor. De esta manera, la relatividad enseña que el tamaño y la forma de los objetos, así como la marcha de los relojes, depende del movimiento: el mundo relativista es notablemente más complejo y rico que el mundo de la física clásica. Ya veremos más adelante cómo estos resultados se enriquecen aún más en la teoría general de la relatividad.
En 1907 Einstein inició la preparación de un artículo de revisión sobre la
teoría de la relatividad que le fue solicitado. Poco había sido contribuido
por otros autores al desarrollo de esta teoría; las primeras contribuciones
importantes a la relatividad no producidas por Einstein se deben a Planck y
a Von Laue; de hecho, Planck fue el primer físico que apreció el valor de esta
teoría e hizo mucho por difundirla, entrando incluso en contacto epistolar con
Einstein, lo que propició el surgimiento de una amistad y relación de mutuo
aprecio que duró el resto de sus vidas. En 1907 apareció el trabajo de Hermann
Minkowski (matemático ruso- alemán [1864-1909] que había sido profesor de Einstein
en el ETH) en que le dio a la teoría de la relatividad la forma
matemática que hoy es usual 9 y que le abrió camino a
Einstein para el desarrollo ulterior de la teoría general.
Un día, sentado en su escritorio en la oficina de patentes, pensando un poco sobre su artículo de revisión, Einstein tuvo lo que años más tarde llamó la idea más feliz de su vida y que le condujo a una primera versión, aún provisional e incompleta, de lo que con el tiempo constituiría la teoría general de la relatividad. Este pensamienfo feliz constituye la base del principio de equivalencia. Supongamos dos observadores iguales encerrados en sendos elevadores y haciendo cada uno el mismo experimento físico; uno de los elevadores está quieto, pero sumergido en un campo gravitatorio que actúa hacia abajo; sobre el otro elevador no actúa ningún campo externo, pero es jalado con aceleración constante hacia arriba (Figura 1). Pensando un poco advertimos que no hay diferencia observable entre los dos casos: ambos experimentadores obtendrán exactamente los mismos resultados de sus experimentos, cualesquiera que ellos sean. En otras palabras, los efectos (locales) de un campo gravitatorio son exactamente equivalentes a los que produce una aceleración uniforme apropiada. En breves palabras, tomadas del propio Einstein: "Si una persona cae libremente, no siente su propio peso." Esta equivalencia se cumple debido sólo a que la masa inercial de los cuerpos (es decir, la masa que se opone a los cambios de movimiento) es exactamente igual a su masa gravitatoria (es decir, a la masa que es atraída por la gravitación), pues debido a ello todos los cuerpos se aceleran igual en un mismo campo gravitatorio y, por lo tanto, podemos sustituir a este último por la aceleración común que produce. Por esta razón Einstein elevó a la categoría de principio el hecho empírico —y no explicado por la física clásica— de la igualdad entre los dos tipos de masas.10
Con el principio de equivalencia en la mano. Einstein podía tratar de extender el principio de relatividad a movimientos acelerados: no hay razón a priori para que el principio de relatividad no valga para cualquier forma de movimiento, y el poder eliminar el campo gravitatorio introduciendo una aceleración en su lugar permitía incluir en la teoría no sólo la óptica, sino la gravedad. La conclusión más inmediata a la que llegó fue que una teoría general de la relatividad le debería permitir construir una teoría de la gravitación.
Veamos otra consecuencia simple del principio de equivalencia, aplicado al caso de la luz. Supongamos que al elevador que se mueve aceleradamente hacia arriba entra un haz de luz que viaja sobre la horizontal; durante el tiempo que el haz tarda en cruzar al elevador, éste se mueve hacia arriba. El observador dentro del elevador (que siente que se encuentra dentro de un campo gravitatorio) observa la desviación del haz y concluye que la luz se desvía al pasar por un campo gravitatorio (Figura 1). En 1907 Einstein pensó que este efecto de desviación de la luz por la gravedad era demasiado pequeño para ser observado y no le dio mayor importancia. Sin embargo, algunos años más tarde, sería precisamente este efecto el que lo llevaría al pináculo de la fama.
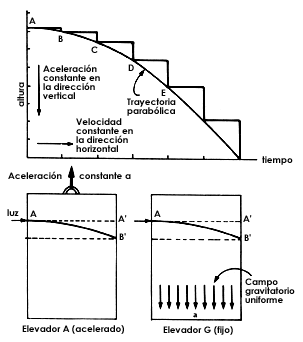
Figura 1. El principio de equivalencia y la desviación de la luz. En la parte superior se muestra cómo al componer un movimiento horizontal de velocidad constante con uno vertival de aceleración constante (y velocidad creciente) se produce una trayectoria parabólica. Un ejemplo simple de este movimiento es el de un proyectil lanzado horizontalmente que cae por la acción de su peso.
En la parte inferior se muestra el principio de equivalencia y su efecto sobre un rayo de luz. El elevador A sube con aceleración constante a, por lo que el rayo de luz sigue una trayectoria parabólica y cae en el punto B´, y no en A´, que es donde caería si el elevador no se moviera. El elevador G está fijo sobre la tierra, pero sujeto a su campo gravitatorio, el que produce una aceleración a hacia abajo. Por el principio de equivalencia, el rayo luminoso que entra por A se desvía y cae en B´.
Una consecuencia adicional que aparece ya en el trabajo de 1907 se refiere al corrimiento de la luz hacia el rojo. Así como hay una dilatación del tiempo debida a la velocidad, también la hay debida a la aceleración —al menos por la velocidad producida por la aceleración— del principio de equivalencia sigue que debe haber una dilatación del tiempo debida a la presencia de un campo gravitatorio. Supongamos ahora que observamos luz que nos llega del Sol; puesto que los átomos que la produjeron están sujetos a un intenso campo gravitatorio, la luz que recibimos debe ser más roja (es decir, de menor frecuencia o de paso más lento) que la generada con los mismos métodos en la Tierra. Retornaremos a este tema en el próximo capítulo.
El siguiente comentario al tema de la deflexión de la luz parece oportuno. Basado en su hipótesis de que la luz está formada por corpúsculos, Newton llegó a sugerir en su Optica la posibilidad de que la gravitación afectara a distancia la trayectoria rectilínea de un rayo luminoso. La predicción de Einstein en sus trabajos iniciales sobre la desviación de la luz corresponde a esta "deflexión newtoniana", de origen puramente gravitatorio. Sin embargo, cuando en 1915 Einstein dio forma final a su obra maestra Fundamentos de la teoría general de la relatividad, trabajo en que la teoría alcanza su forma definitiva, mostró que además del efecto newtoniano hay otro, puramente relativista, de magnitud igual al anterior, de tal manera que la teoría final predice el doble de lo que las variantes iniciales sugerían. Fue precisamente este punto el que pusieron a prueba las famosas mediciones del eclipse solar de 1919. Pero sobre de estos temas hablaremos más tarde.
Es lugar común hablar del año 1905 como el año milagroso de Einstein. Y el asombro es justo; hemos visto cómo en el curso de tan sólo cuatro meses de ese año funda las teoría cuánticas de la luz, del movimiento browniano y de la relatividad. Cualquiera de estos resultados es suficiente para llenar de satisfacción a un físico respetable y al menos dos de ellos pueden legítimamente ser considerados una revolución en la física. Lo que normalmente no se comenta es cómo poco tiempo después Einstein se acerca mucho a una repetición del milagro: en el curso de menos de un año —de fines de 1906 a septiembre de l907— Einstein da dos nuevos pasos adelante de singular importancia y novedad: nos referimos a la teoría cuántica de los calores específicos (es necesario cuantizar la materia, y no tan sólo el campo de radiación) y al principio de equivalencia y sus primeras consecuencias. Otros dos resultados suficientes para llenar la vida de nuestro hipotético respetable investigador. Uno no puede menos que hacer suya la pregunta de Pais: 11 "¿Pero es que este hombre nunca va a parar?"
En 1909 seproduce la eclosión social de Einstein. A mediados de año se le notifica que con motivo del 350 aniversario de la fundación por Calvino de la Universidad de Ginebra, se ha acordado concederle un doctorado honoris causa; el honor lo recibe junto con María Curie y Wilhelm Ostwald, entre un centenar de personas. Poco tiempo después recibe la invitación de la Sociedad Alemana de Ciencias Naturales para presentar una ponencia en su próxima reunión de Salzburgo, que mencionamos un poco más arriba. Ésta fue la primera oportunidad que tuvo Einstein de entrar en contacto con físicos en activo: ahí se encontró por vez primera con Planck, Wien, Sommerfeld, Born, e incluso con Ludwig Hopf, quien pronto sería su asistente. Finalmente, deja su puesto de la Oficina de Patentes, en el tercer piso de la Oficina de Correos y Telégrafos y parte para Zurich.
Einstein tiene treinta años; ha vivido fuera de los círculos académicos y ha escrito dos trabajos que revolucionan la física clásica; tiene en maduración el germen de lo que devendrá en pocos años más en una nueva teoría de la gravitación y una nueva visión del mundo físico. Se dirige a Zurich a ocupar su primera plaza como profesor universitario.¿¿¿¿
NOTAS 1En su versión general, filosófica, este principio se conoce con el nombre de navaja de Occam, William de Occam (c, 13280-1349) fue un importante pensador y reformador inglés, que se opuso al poder del papado. Su famoso dictum pluralites non est ponenda sine necessitate —no debe proponerse lo complejo sin necesidad— es citado muy frecuentemente 2 Valgan algunas aclaraciones adicionales para el lector interesado. Planck encontró que los paquetes de energía que el cuerpo puede absorber o emitir tienen un tamaño que crece con la frecuencia f de la luz, de tal manera que podía escribir un cuanto de energía electromagnética E en la forma E = h f, en donde h es una constante, la misma para todos los cuantos, y que Planck pudo determinar comparando sus resultados con los del experimento. A la cantidad h se le llama constante de Planck y es una de las constantes fundamentales de la naturaleza, junto con la masa y la carga del electrón y la velocidad de la luz. Esta fórmula nos explica por qué en efecto el horno no es azul. Luz de baja frecuencia se emite por paquetes de baja energía; pero para emitir un paquete de muy alta frecuencia es necesario reunir muy alta energía en un sólo paquete, cosa que es poco probable que suceda. Para explicaciones más detalladas, consultar la bibliografía al final del libro.
3 Las fluctuaciones son una medida estadística de los cambios irregulares que ocurren en una cantidad determinada por un proceso muy complejo. Por ejemplo, la población de la República Mexicana crece con los años, pero no lo hace regularmente, sino fluctuando alrededor de una curva estadística. Análogamente, la presión de un gas sobre las paredes del recipiente que lo contiene se debe al golpeteo de las moléculas sobre ellas; esta presión es relativamente fija en condiciones constantes, pero fluctúa, creciendo y decreciendo constantemente. Su valor promedio es el que permanece constante.
4 En forma simultánea a Einstein el físico polaco Marian Ritter von Smolan-Smoluchowski (1872-1917) realizó investigaciones sobre el movimiento browniano tanto teóricas como experimentales. El trabajo de estos dos pioneros se superpone considerablemente y a ambos se les considera fundadores de la teoría del movimiento browniano, que fue la primera teoría física de los procesos estocásticos, es decir, azarosos.
5 De hecho en la formulación dada arriba estamos combinando los dos principios de la relatividad. Estrictamente, el primer principio de Einstein afirma sólo que c es independiente de la velocidad de la fuente emisora.
6 Por ejemplo, cuando un núcleo de uranio se rompe en fragmentos menores, la masa total de todos ellos es ligeramente menor que la del núcleo inicial; la diferencia de masas es liberada como energía. Esta energía es aproximadamente un millón de veces la que se obtendría de quemar una masa igual de leña; por eso se dice que la energía útil nuclear es como un millón de veces la energía química o molecular correspondiente.
7 A este fenómeno se le conoce como contracción de Lorentz (o de FitzGerald Lorentz) y lo reencontraremos en el próximo capítulo. Antes que Einstein derivara este efecto como un resultado de la cinemática relativista, fue propuesto independientemente por el físico holandés Hendrik Lorentz (18531928) para explicar los resultados negativos del experimento de Michelson y Morley. Con su teoría, Lorentz pudo también predecir la variación de la masa con la velocidad. Lorentz fue el primero que propuso que los átomos contenían partículas cargadas (en 1890) y que ellas, al oscilar dentro del átomo, producían la luz radiada.
8 Pion, muon y neutrino no son sino tres tipos diferentes de las llamadas partículas elementales, de las cuales se conocen varios cientos. Otras partículas elementales son, por ejemplo, el electrón, el protón y el neutrón. También se considera al fotón como una partícula elemental. En el presente contexto, como en general en la física, espontáneo significa sin causa aparente o conocida; no significa sin causa.
9 Nos referimos a la noción del espacio-tiempo de cuatro dimensiones. Minkowski hizo ver que en la rlelatividad lo que tiene sentido profundo es un elemento matemático, el espacio- tiempo que combina las nociones de espacio y de tiempo; cada una de ellas por separado es insuficiente. En alguna forma esto es análogo a lo que pasa con las dos leyes no relativistas independientes de conservación de la masa y de la energía, que quedan sustituidas por una sola, la conservación de la energía relativista.
10 En el Apéndice 2 se describe un experimento simple para mostrar el principio de equivalencia.
11 En el libro citido en la bibliografía al final.